Термины, определения

Очереди как элементы упорядочения процессов в производстве, сбыте и потреблении товаров имеют место во всех сферах маркетинговой деятельности. Основные параметры очереди характеризуются свойствами входящего потока требований, потока обслуживания и дисциплины очереди. Расчеты систем обслуживания производятся с целью уменьшения нагрузок на обслуживающие приборы, уменьшения длины очередей, снижения затрат на обслуживание, увеличения пропускной способности системы и т. п. Основные показатели работы систем: длина очереди, время нахождения требования в системе, доля времени, в течение которого прибор бывает свободен.

Наиболее универсальной моделью системы массового обслуживания является модель с пуассоновским входящим потоком и экспоненциальным распределением времени обслуживания.

Распределение Пуассона – распределение вероятностей случайных величин x_i, принимающих целые неотрицательные значения k = 0,1,2,…,n с вероятностями [3, 4, 9, 20]

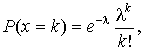(5.1)

где λ > 0 – параметр.

Математическое ожидание, дисперсия и моменты более высоких порядков равны λ. Сумма независимых случайных величин X_i, имеющих распределение Пуассона с параметрами λ_i, подчиняется также распределению Пуассона с параметрами ∑λ_i. Это предельное распределение безгранично делимо: если сумма случайных величин имеет распределение Пуассона, то каждое слагаемое можно представить как распределенное по закону Пуассона.

Поток событий – это последовательность событий, происхо-дящих одно за другим в случайные моменты времени.

Поток называют стационарным, если вероятность появления некоторого числа событий в какой-то промежуток времени зависит только от величины временного промежутка.

Поток событий называют потоком без последействия, если для любых не перекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

Поток событий называют ординарным, если вероятность попадания на элементарный участок Δt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Если поток обладает всеми тремя свойствами, он называется простейшим (пуассоновским).

Время обслуживания (как и время между поступлениями в систему обслуживания), когда поток обслуживания (или поступления в систему) обладает этими тремя свойствами, распределено по экспоненциальному закону

g(t) = μe^–μt, (5.2)

где μ – параметр, величина, обратная среднему времени обслуживания одной заявки: μ = 1/m_{t обсл}.

Величина λ должна быть меньше, чем μ, иначе очередь будет расти до бесконечности по геометрической прогрессии.

Когда входящий поток – пуассоновский, а время обслуживания распределено по экспоненциальному закону, при одном приборе обслуживания, система обозначается М/М/1. Буква G в обозначении системы массового обслуживания означает произвольное распределение, E_k – распределение Эрланга порядка k, D – детерминированный поток (равные промежутки времени между поступлениями требований в систему или применительно к прибору обслуживания – неслучайное и одинаковое время обслуживания для всех требований). Например, E₃/G /2 означает, что входящий поток системы – эрланговский третьего порядка, поток обслуживания имеет произвольное распределение времени обслуживания, число обслуживающих приборов равно двум.