I этап: Анализ задачи
Назначение этапа:
– понять в целом ситуацию, описанную в задаче;
– выделить условия и требования;
– назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.
Анализ задачи всегда направлен на её требование, т.е. на вопрос текстовой задачи.
Приёмы анализа содержания задачи:
- задать специальные вопросы и ответить на них:
Ø о чём задача?
Ø можно ли сразу ответить на вопрос задачи?
Ø что требуется найти в задаче?
Ø что означают те или иные слова в тексте?
Ø что в задаче неизвестно?
Ø что является искомым?
Ø и т.д.
Рассмотрим задачу:
«По дороге в одном и том же направлении идут два мальчика. Вначале расстояние между ними было 2 км, но так как скорость идущего впереди мальчика 4 км/ч, а скорость второго 5 км/ч, то второй нагоняет первого. С начала движения до того, как второй мальчик догонит первого, между ними бегает собака со скоростью 8 км/ч. От идущего позади мальчика она бежит к идущему впереди, добежав, возвращается обратно и так бегает до тех пор, пока мальчики не окажутся рядом. Какое расстояние пробежит за всё это время собака?»
- перефразировка текста задачи:
замена данного в задаче описания некоторой ситуации другим, сохраняющим все отношения, связи, качественные характеристики, но более явно их выражающим.
Это достигается в результате
– отбрасывания несущественной, излишней информации;
– замены описания некоторых понятий соответствующими терминами и, наоборот, замены некоторых терминов описанием содержания соответствующих понятий;
– преобразования текста задачи в форму, удобную для поиска плана решения.
Особенно эффективно использование данного приёма в сочетании с разбиением текста задачи на смысловые части.
Результатом перефразировки должно быть выделение основных ситуаций.
Переформулируем рассмотренную задачу:
Первая часть: «скорость одного мальчика 4 км/ч, а скорость догоняющего его второго мальчика 5 км/ч»
Вторая часть: «расстояние, на которое мальчики сблизились, 2 км.»
Третья часть: «время движения мальчиков – это время, в течение которого второй мальчик догонит первого, т.е. в течение которого второй мальчик пройдёт на 2 км больше, чем первый»
Четвёртая часть: «скорость, с которой бежит собака, 8 км/ч. Время движения собаки равно времени движения мальчиков до встречи»
Требование: «определить расстояние, которое пробежала собака»
- построение вспомогательной модели задачи:
Ø таблица
| объекты | скорость | время | расстояние |
| 1-й м. 2-й м. собака | 4 км/ч 5 км/ч 8 км/ч |  ? ч.
? ч. одинаковое
? ч. ? ч.
? ч. одинаковое
? ч.
| ? км. ? км., на 2 км. больше 1-го м. ? км. |
Ø схематический чертёж
 8 км/ч
8 км/ч
 5 км/ч 4 км/ч
5 км/ч 4 км/ч
2 км
После построения вспомогательной модели необходимо проверить:
1)все ли объекты задачи показаны на модели;
2)все ли отношения между объектами отражены;
3)все ли числовые данные приведены;
4)есть ли вопрос (требование) и правильно ли он указывает искомое?
(лекция 8)
3.4. Приёмы поиска плана решения задачи и его выполнение.
II этап: Поиск и составление плана решения задачи
Назначение этапа:
– установить связь между данными и исходными объектами;
– наметить последовательность действий.
Приёмы поиска плана решения задачи:
- разбор задачи по тексту проводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от её вопросов.
Ø при разборе задачи от данных к вопросу нужно выделить в тексте задачи два данных и на основе знания связи между ними (такие знания должны быть получены при выполнении первого этапа решения) определить, какое неизвестное может быть найдено по этим данным и с помощью какого арифметического действия. Считая это неизвестное данным, надо вновь выделить два взаимосвязанных данных, определить неизвестное, которое может быть найдено по ним, а также соответствующее арифметическое действие и т.д. пока не будет выяснено действие, выполнение которого приводит к получению искомого.
Проведём такой разбор по тексту задачи:
«На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?»
| 1) | известно | 6 ч. по 56 км/ч | |
| можно узнать | расстояние, которое поехал турист за 6 ч. | 6 · 56 = 336 (км) | |
| 2) | известно | 336 км. в 4 раза меньше оставшегося | |
| можно узнать | расстояние, которое осталось проехать | 336 · 4 = 1344 (км) | |
| 3) | известно | 336 км. и 1344 км. | |
| можно узнать | весь путь | 336 + 1344 = 1680 (км) |
Ø при разборе задачи от вопроса к данным нужно обратить внимание на вопрос задачи и установить (на основе информации, полученной при анализе текста задачи), что достаточно узнать для ответа на вопрос задачи. Для чего нужно обратиться к условиям и выяснить, есть ли для этого необходимые данные. Если таких данных нет или есть только одно данное, то установить, что нужно знать, чтобы найти недостающее данное (недостающие данные), и т.д. Потом составляется план решения задачи. Рассуждения при этом проводятся в обратном порядке.
- разбор задачи по вспомогательной модели может быть проведён по-разному, – в результате получаются различные арифметические способы её решения.
Ø схематический чертёж
 шапка
шапка
|
шарф
|
свитер
I способ:
1) 1200 – 100 – 400 – 100 = 600 (гр.)
2) 600 : 3 = 200 (гр.) – израсходовали на шапку;
3) 200 + 100 = 300 (гр.) – израсходовали на шарф;
4) 300 + 400 = 700 (гр.) – израсходовали на свитер.
II способ:
1) 1200 – 300 = 900 (гр.)
2) 900 : 3 = 300 (гр.) – израсходовали на шарф
3) 300 – 100 = 200 (гр.) – израсходовали на шапку
4) 300 + 400 = 700 (гр.) – израсходовали на свитер
III способ:
1) 1200 – 400 + 100 = 900
2) 900 : 3 = 300 (гр.) – израсходовали на шарф
3) 300 + 400 = 700 (гр.) – израсходовали на свитер
4) 300 – 100 = 200 (гр.) – израсходовали на шапку
Ответ: 200 гр., 300 гр., 700 гр.
Ø таблица
«Сколько деталей получится из 36 кг. металла, если из 12 кг. получается 8 таких же деталей?»
| масса одной детали | количество деталей | масса всех деталей |
| одинаковая | 8 шт. | 12 кг |
| ? шт. | 36 кг |
I способ:
1) 12 : 8 = 1,5 (кг.) – масса одной детали
2) 36 : 1,5 = 24 (шт.) – количество деталей.
II способ: (прямая пропорциональность)
1) 36 : 12 = 3 – во столько раз масса 8 деталей меньше, чем масса искомых
2) 8 · 3 = 24 (шт.) – количество деталей
III способ: (пропорция)
8 шт. – 12 кг.
х шт. – 36 кг.
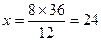 (шт.) – количество деталей
(шт.) – количество деталей
Ответ: 24 детали.
Ø краткое условие
«В первый день туристы прошли 120 км., во второй – ¾ пройденного в первый день, а в третий день на 35 км. больше, чем во второй. Сколько километров прошли туристы за три дня?»
 I день – 120 км.
I день – 120 км.
 II день – ? км., это ¾ от ? км.
II день – ? км., это ¾ от ? км.
III день – ? км., на 35 км. больше, чем
1) 120 : 4 · 3 = 90 (км.) – во второй день
2) 90 + 35 = 125 (км.) – в третий день
3) 120 + 90 + 125 = 335 (км.) – прошли за три дня
Ответ: 335 километров.
(лекция 9)
III этап: Осуществление плана решения задачи
Назначение этапа:
– выполнить все действия в соответствии с планом;
– найти ответ на требование задачи.
Приёмы осуществления плана решения задачи:
Для текстовых задач, решаемых арифметическим методом, используются следующие приёмы:
- запись по действиям с пояснением;
- запись по действиям без пояснения;
- запись по действиям с вопросами;
- запись в виде выражения.
Рассмотрим примеры различных записей плана решения задачи:
«На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?»
- запись решения по действиям с пояснением к каждому действию:
1) 56 · 6 = 336 (км) – турист проехал за 6 ч.
2) 336 · 4 = 1344 (км) – осталось проехать туристу
3) 336 + 1344 = 1680 (км) – должен был проехать турист.
- запись решения по действиям без пояснения:
1) 56 · 6 = 336 (км)
2) 336 · 4 = 1344 (км)
3) 336 + 1344 = 1680 (км)
- запись решения по действиям с вопросами:
1) сколько километров проехал турист на поезде за 6 часов?
56 · 6 = 336 (км)
2) сколько километров осталось проехать туристу?
336 · 4 = 1344 (км)
3) сколько километров турист должен был проехать?
336 + 1344 = 1680 (км)
- запись решения в виде выражения:
Запись решения в этой форме осуществляется поэтапно:
– сначала записываются отдельные шаги в соответствии с планом,
– затем составляется выражение и находится его значение.
Так, для рассматриваемой задачи эта форма записи имеет вид:
56 · 6 (км) – расстояние, которое проехал турист на поезде за 6 ч
56 · 6 · 4 (км) – расстояние, которое осталось проехать туристу
56 · 6 + 56 · 6 · 4 (км) – путь, который должен проехать турист
56 · 6 + 56 · 6 · 4 = 1680 (км)
Пояснения к действиям можно не записывать, а давать их в устной форме. Тогда запись решения задачи примет вид:
56 · 6 + 56 · 6 · 4 = 1680 (км)
3.5. Приёмы проверки решения задачи.
IV этап: Проверка решения задачи.
Назначение этапа:
установить правильность или ошибочность выполнения решения.
Приёмы проверки решения задачи:
ü установление соответствия между результатом и условиями задачи;
ü решение задачи другим способом.
1. установление соответствия между результатом и условиями задачи:
Для этого найденный результат вводится в текст задачи и на основе рассуждений устанавливается, не возникает ли при этом противоречия.
Проверим, используя данный приём, правильность решения задачи о движении туриста.
Мы установили, что турист должен был всего проехать 1680 км. Пусть теперь этот результат будет одним из данных задачи. Далее, как известно, за 6 ч турист проедет 336 км (56 · 6 = 336) и ему останется проехать 1680 – 336 = 1344 (км). Согласно условию задачи это расстояние должно быть в 4 раза больше того, которое турист проехал на поезде за 6 ч. Проверим это, разделив 1344 на 336. Действительно, 1344 : 336 = 4. Следовательно, если найденный результат подставить в условие задачи, то противоречий с другими данными, а именно отношением «быть больше в 4 раза», не возникает. Значит, задача решена верно.
При использовании данного приёма проверяются все отношения, имеющиеся в задаче, и если устанавливается, что противоречия не возникает, то делают вывод о том, что задача решена верно.
2. решение задачи другим способом:
Пусть при решении задачи каким-то способом получен некоторый результат. Если её решение другим способом приводит к тому же результату, то можно сделать вывод о том, что задача была решена верно.
Заметим, что если задача решена первоначально арифметическим способом, то правильность её решения можно проверить, решив задачу алгебраическим методом.
Не следует также думать, что без проверки нет решения текстовой задачи. Правильность решения обеспечивается прежде всего чёткими и логичными рассуждениями на всех других этапах работы над задачей.
(лекция 10)
3.6. Моделирование в процессе решения текстовых задач.
Текстовая задача – это словесная модель некоторого явления (ситуации, процесса). Чтобы решить задачу, надо перевести её на язык математических действий, т.е. построить её математическую модель.
Математическая модель – это описание какого-либо реального процесса на языке математических понятий, формул и отношений.
Математическая модель ТЗ:
 |  |
если задача решается
| арифметическим методом: выражение, либо запись по действиям | алгебраическим методом: уравнение, либо система уравнений |
Этапы математического моделирования:
I этап –это перевод условий задачи на математический язык; при этом выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними;
II этап– внутримодельное решение, т.е. нахождение значения выражения, выполнение действий, решение уравнения (или системы уравнений);
III этап – интерпретация, т.е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача.
Пример:
«В одном вагоне электропоезда было пассажиров в 2 раза больше, чем в другом. Когда из первого вагона вышли 3 человека, а во второй вагон вошли 7 человек, то в обоих вагонах пассажиров стало поровну. Сколько пассажиров было в каждом вагоне первоначально?»
I этап: составление уравнения.
Пусть х первоначальное число пассажиров во втором вагоне, тогда число пассажиров в первом вагоне – 2х. Когда из первого вагона вышли 3 человека, в нём осталось 2х – 3 пассажира, а во второй вагон вошли 7 человек, в нём стало х + 7 пассажиров. Так как в обоих вагонах пассажиров стало поровну, то получаем уравнение 2х – 3 = х + 7
II этап: решение уравнения.
2х – 3 = х + 7
2х – х = 3 + 7
х = 10
III этап: перевод полученного решения.
Во втором вагоне первоначально было 10 человек, а в первом 10 · 2 = 20 человек
Самым сложным этапом при математическом моделировании является I этап: перевод текста задачи с естественного языка на математический. Для упрощения этого этапа строят вспомогательную модель – схему, таблицу и др.
Дата добавления: 2016-02-16; просмотров: 24440;
