Числовые промежутки

название	неравенство, определяющее множество решений	обозначение	изображение
числовой отрезок от а до в (замкнутый промежуток)	а ≤ х ≤ в	[а; в]
	а в
числовой интервал от а до в (открытый промежуток)	а < х < в	(а; в)
	а в
открытый слева числовой промежуток от а до в	а < х ≤ в	(а; в]
	а в
открытый справа числовой промежуток от а до в	а ≤ х < в	[а; в)
	а в
числовой луч от а до положительной бесконечности (+ ∞)	х ≥ а	[а; + ∞)
	а + ∞
открытый числовой луч от а до (+ ∞)	х > а	(а; + ∞)
	а + ∞
числовой луч от отрицательной бесконечности (– ∞) до а	х ≤ а	( – ∞; а]
– ∞ а
открытый числовой луч от отрицательной бесконечности (– ∞) до а	х < а	(– ∞; а)
– ∞ а

Два неравенства называются равносильными, если множества их решений совпадают.

Пример:

2х + 7 > 10 2х > 10 – 7 2х > 3 х > 3 : 2 х > 1,5	– 4х < – 6 4х > 6 х > 6 : 4 х > 1,5
											х 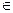(1,5; + ∞)
		1,5

Вывод: данные неравенства равносильны.

Теоремы равносильности:

Теорема 1:

если к обеим частям неравенства f(x) > g(x) прибавить выражение h(x), определённое на ОДЗ неравенства, то получим неравенство f(x) + h(x) > g(x) + h(x) равносильное данному.

Следствие 1:

если к обеим частям неравенства f(x) > g(x) прибавить одно и то же действительное число d, то получим неравенство f(x) + d > g(x) + d равносильное данному.

Следствие 2:

если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.

Теорема 2:

если обе части неравенства f(x) > g(x) умножить на выражение h(x) > 0, определённое на ОДЗ неравенства, то получим неравенство f(x) × h(x) > g(x) × h(x) равносильное данному.

Следствие 3:

если обе части неравенства f(x) > g(x) умножить на одно и то же положительное действительное число d, то получим неравенство f(x) × d > g(x) × d равносильное данному.

Теорема 3:

если обе части неравенства f(x) > g(x) умножить на выражение h(x) < 0, определённое на ОДЗ неравенства, то получим неравенство f(x) × h(x) < g(x) × h(x) равносильное данному.

Следствие 4:

если обе части неравенства f(x) > g(x) умножить на одно и то же отрицательное действительное число d, то получим неравенство f(x) × d < g(x) × d равносильное данному.

I вариант	II вариант
Дайте определения следующим понятиям:
а) область определения выражения; б) тождество; в) уравнение; г) неизвестное делимое; д) неизвестное вычитаемое.	а) значение выражения; б) тождественное преобразование; в) корень уравнения; г) неизвестный делитель; д) неизвестное уменьшаемое.
Запишите следующие выражения с помощью математического языка:
а) разность числа 37 и суммы 14 и 29; б) сумма частного чисел 237 и 14 и разности чисел 12 и 5; в) частное суммы 34 и 40 и разности 78 и 45.	а) разность суммы 26 и 17 и числа 5; б) сумма произведения 9 и 13 и разности 43 и 68; в) произведение частного чисел 81 и 9 и суммы 3 и 17.
Запишите решение задачи в виде выражения, а затем найдите его значение:
На турбазу прибыли в один день 150 туристов, на другой день 170. Чтобы совершить поход, 200 туристов разбились на группы, по 20 человек в каждой, а остальные по 15 человек в группе. Сколько получилось групп?	В мастерской за 5 дней сшили 2000 фартуков. Сколько фартуков сошьют в мастерской за 8 дней, если в день будут шить на 50 фартуков больше?
Среди следующих записей выделите числовые выражения, выражения с переменной, тождества, числовые равенства и числовые неравенства:
а) 1,2х + 3у – 8; б) 0,3х + 7,8у = 9; в) 25 + (8,4 : 0,03) · 1,2; г) 24 + (0,75 : 0,2) = 24,15; д) 3(х – 4) + (1 + х) < 2; е) 6(у – 3) = 6у – 18; ж) 32 + – ) : 14; з) 25 – 7 > 43.	а) 20 + 4z = 4(5 + z); б) 26 + 19 < 21; в) 25 × ( + 16 : 3; г) 3,7х – 4у + 12; д) 5,9у – 3,7х = 112; е) (2,07 : 0,9) – 36 · 4,8; ж) (81 : 0,9) – 67 = 23; з) (х + 5) – 1,7(8 – у) > 9.
Расставь скобки так, чтобы равенства были верными:
31 – 10 – 3 = 24	54 – 12 + 8 = 34
Поставь вместо * знаки действий так, чтобы получились верные равенства:
3 * 6 * 2 = 9	9 * 3 * 6 = 18
Сформулируйте следующие теоремы:
а) теорема 1 о равносильности уравнений; б) теорема 2 о равносильности неравенств.	а) теорема 2 о равносильности уравнений; б) теорема 1 о равносильности неравенств.
Решите уравнение:
а) 5(3х – 1)(4х + 7) = 0 б) |7 – 8х| = 4	а) – 2(1 + х)(12х + 4) = 0 б) |3х + 4| = –1
9. На координатной прямой с единичным отрезком три клеточки постройте следующие точки: F(– 4); K(1,5); T(– 2,5); H(3).	9. На координатной прямой с единичным отрезком две клеточки постройте следующие точки: G(– 4,5); N(3); U(– 2); S(5,5).
10. Запишите неравенства, множества решений которых изображено на рисунке:
а)   – 6 – 3	в)   2 9	а)   – 4 7	в)   5 12
б)   11,4	г)   – 8	б)   – 3,5	г)
11. Изобразите на координатной прямой множество решений неравенства:
а) а < х < в б) х ≥ в	в) – а ≤ х < в г) х < – а	а) а ≤ х ≤ в б) х > – в	в) – а < х ≤ в г) х ≤ а

(лекция 2)