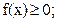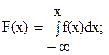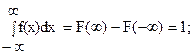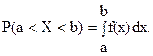Плотность распределения вероятностей и числовые характеристики случайной величины
Плотностью распределения вероятностей непрерывной случайной величины ( дифференциальной функцией распределения ) называют первую производную от интегральной функции распределения: f(x)=F’(X). Из этого определения и свойств функции распределения следует, что
Математическим ожиданием непрерывной случайной величины X называют число
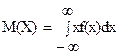
Дисперсия непрерывной случайной величины X определяется равенством
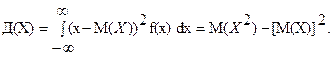
Пример 79. Плотность распределения времени Т сборки РЭА на поточной линии

Найти коэффициент A, функцию распределения времени сборки РЭА и вероятность того, что время сборки будет находиться в пределах интервала (0,1А).
Решение. На основании свойства функции распределения случайной величины
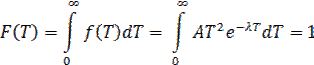
Дважды интегрируя по частям, получаем
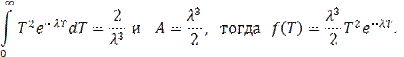
Функция распределения равна
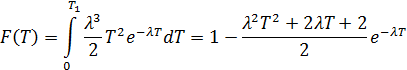
Вероятность того, что время сборки РЭА не выйдет за пределы (0; 1/λ):
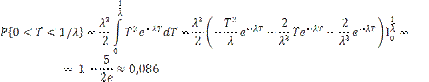
Пример 80. Плотность вероятности отклонения выходного сопротивления блока РЭА от номинального значения R0 в пределах поля допуска 2δ описывается законом
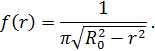
Найти математическое ожидание и дисперсию отклонения сопротивления от номинального значения.
Решение.
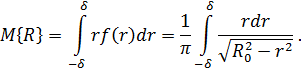
Поскольку подынтегральная функция нечетная и пределы интегрирования симметричны относительно начала координат, интеграл равен 0.
Следовательно, M{R} = 0.
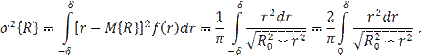
Сделав подстановку r = a sin x, получим
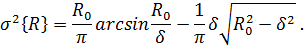
Пример 81. Задана плотность распределения непрерывной случайной величины X:
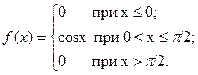
Найти: 1. F(x); 2. M(X); 3. Д(X).
Решение.1. Для отыскания F(x) используем формулу 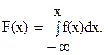
Если 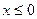 , то
, то
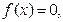 а
а 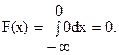
Если 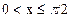 , то
, то
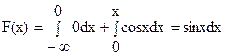
Если 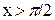 ,то f(x)=0, а
,то f(x)=0, а
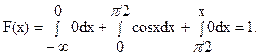
Итак,
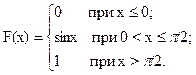
2. 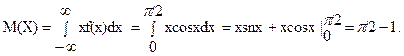
3. 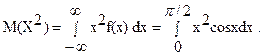
Дважды интегрируя по частям получим:
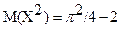 , тогда
, тогда 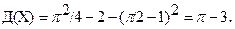
82. Найти f(x), M(X), Д(X) в задачах 74, 75.
83. Задана плотность распределения непрерывной случайной величины X:
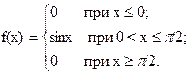
Найти функцию распределения F(x).
84. Плотность распределения непрерывной случайной величины X задана на всей оси Ох равенством 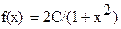 . Найти постоянный параметр С.
. Найти постоянный параметр С.
85. Случайная величина X в интервале (—3, 3) задана плотностью распределения 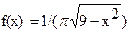 ; вне этого интервала
; вне этого интервала 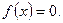
а) Найти дисперсию X;
б) что вероятнее: в результате испытания окажется X<1 или X>1?
86. Найти дисперсию случайной величины X, заданной функцией распределения
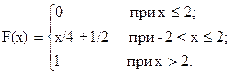
87. Случайная величина задана функцией распределения
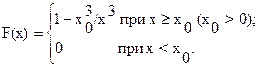
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение X.
Дата добавления: 2016-03-15; просмотров: 2995;