Вероятностей случайной величины

Функцией распределения вероятностей (интегральной функцией распределения) случайной величины называют функцию F(x), определяющую для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x)=P(X<x).

Из определения следует, что эта функция принимает значения от 0 до 1, причем 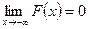, , 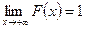не может убывать, а вероятность попадания случайной величины X на интервал (a,b) вычисляется по формуле:

P(a<X<b)=F(b)-F(a).

Пример72. Количество блоков РЭА, собираемых на различ­ных операциях на конвейерной линии за один и тот же период времени, задано законом распределения:

х_£ 2 4 7

p_t 0,5 0,3 0,2

Определить интегральную функцию F (х), характеризующую вероятность сборки требуемого количества блоков по операциям и построить ее график.

Решение.Если X ≤ 2, то F (х) = 0, так как значений, меньших 2, X не принимает. Если 2<Х≤4, то F(x)=0,5 пo условию примера. Если 4 < X ≤ 7, F (х) = 0,8. Действительно, X может принять значение 2 с вероятностью 0,5 и значение 4 с вероятностью 0,3. Сле­довательно, одно из этих значений, без­различно какое, X принимает (по теоре­ме сложения вероятностей несовместимых событий) с вероятностью 0,8. Если Х>7, то F(х) = 1, так как событие Х≤7 до­стоверно и вероятность его равна еди­нице. Таким образом,

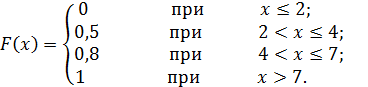
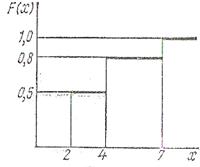
График функции F(x) приведен ниже.

Пример73. Изменение центра группирования погрешности тонкопленочного резистора на точностной диаграмме процесса напыления можно описать интегральным законом распределения:

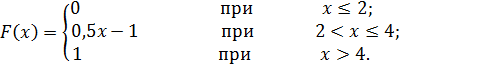
Найти вероятность того, что среднее значение погрешности примет значения: а) меньшее 0,2; б) меньшее 3; в) не меньшее 3; г) не меньшее 5.

Решение. Так как при X ≤ 2 функция F(x)=0то F(0,2) = 0, т. е. Р{Х<0,2}=0.

P {X < 3} = F (3) = (0,5 • 3 - 1) = 0,5.

Так как сумма вероятностей противоположных событий рав­на единице, а события X ≥ 3 и X < 3 противоположны,

P{X≥3}+P{X<3}=1.

Тогда, учитывая, что Р (X < 3) = 0,5, получим Р (X ≥ 3) = 1-0,5 = 0,5, Р {X ≥ 5} + Р{Х < 5} = 1 и учитывая, что приХ>4 P{x}=1получим

P {X≥5} = 1 - P (X<5) = 1 – F (5) = 1 – 1 = 0.

74. Случайная величина X задана на всей оси Ох функцией распределения F (x) = 1/2 + (arctg х)/π. Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (О, 1).

75. Функция распределения непрерывной случайной величины X (времени безотказной работы некоторого устройства) равна F(x)=l-e^-x/T (х≥О). Найти вероятность безотказной работы устройства за время х≥Т.

76. Случайная величина X задана функцией распределения

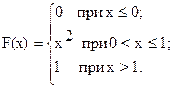
Найти вероятность того, что в результате четырех независимых испытаний величина X ровно три раза примет значение, принадлежащее интервалу (0,25, 0,75).

77. Случайная величина X задана на всей оси Ох функцией распределения F(х)=(1/2)+(1/π)arctg(х/2). Найти возможное значение х₁, удовлетворяющее условию: с вероятностью 1/6 случайная величина X в результате испытания примет значение, большее х₁.

78. Дискретная случайная величина задана законом распределения

X 3 4 7 10

p 0,2 0,1 0,4 0,3

Найти функцию распределения и построить ее график.