Абсолютные и относительные величины в статистике. Виды взаимосвязи относительных величин
С философской точки зрения статистический показатель – это мера, т.е. единство качественного и количественного отражения свойств объективных явлений и процессов в научном сознании. Поскольку статистика изучает массовые явления, статистический показатель – это обобщающая характеристика какого-то свойства совокупности, группы. Этим он отличается от индивидуальных значений, которые называются признаками. Например, средняя продолжительность ожидаемой жизни родившегося поколения людей в стране – статистический показатель. Продолжительность жизни конкретного человека – признак.
Признак – это свойство, присущее единице совокупности. Признак входит в качественное содержание показателя, он существует объективно независимо от того, отражает ли его наука с помощью тех или иных показателей. Например, возраст человека – это его признак, который можно измерять с разной степенью точности – в годах, месяцах, в сутках или охарактеризовать датой рождения.
Показатель – характеристика группы единиц, или совокупности в целом. Его построение зависит от цели исследования и изобретательности статистика. Средний возраст работников фирмы или жителей города – это статистические показатели, дающие возрастную характеристику определенных групп. Другим видом возрастных показателей могут служить ряд распределения людей по возрасту и вычисленные на основе этого ряда системы показателей для характеристики структуры такого ряда и размеров вариации.
Объектами статистического исследования могут быть самые разнообразные явления и процессы. Поэтому чрезвычайно велико и разнообразие статистических показателей. По способу обобщения исходных данных показатели разделяют на две группы:
- абсолютные величины (объемные, количественные, экстенсивные);
- относительные и средние величины (производные, качественные, интенситвные).
Абсолютным показателемявляется такой, который отражает либо суммарное число единиц, либо суммарное свойство объекта. В их составе различают два вида показателей:
1) численность единиц совокупности (так называемый перечневый подсчет);
2) объем признака единиц совокупности (так называемый итоговый подсчет).
Например, при обследовании результатов деятельности совокупности промышленных предприятий их число является перечневым подсчетом, а число рабочих, объем продукции или объем каких-либо других признаков этих предприятий – итоговый.
В зависимости от цели исследования некоторые абсолютные показатели могут выступать в одних случаях как показатели численности совокупности, а в других – как показатели объема признака.
Абсолютные показатели, как правило, выражаются именованными величинами в натуральных единицах измерения: тоннах, штуках, часах, амперах и т.п., в условных единицах: условном топливе, норме-сменах, килономерах пряжи и т.д.; трудовых: человеко-днях, человеко-часах; или в стоимостных единицах: рублях, долларах, евро.
Относительным показателемявляется показатель, полученный путем сравнения, сопоставления абсолютных или относительных показателей в пространстве (между объектами), во времени (по одному и тому же объекту) или сравнения показателей разных свойств изучаемого объекта.
Относительной величинойв статистике называется показатель, который является мерой соотношения двух сопоставляемых статистических характеристик.
Выражаются относительные величины в коэффициентах; в процентах, промилле, продецимилле; в именованных числах.
Различают следующие основные виды относительных величин (ОВ):
1.Относительная величина выполнения плана (задания, договора) отражает степень реализации плановых заданий и вычисляется как отношение фактически достигнутого уровня к плановому заданию:
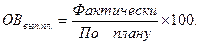
2.Относительная величина динамики – характеризует изменение уровня развития какого-либо явления во времени. Представляет собой отношение данного (отчетного) уровня изучаемого явления к уровню за предшествующий период. Такие показатели называют темпами роста. К относительным показателям динамики принадлежат также темпы прироста, параметры уравнений трендов, коэффициенты колеблемости и устойчивости в динамике, индексные показатели динамики.
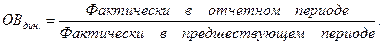
3. Относительная величина планового задания - отношение уровня, запланированного на предстоящий период, к уровню показателя, достигнутому в предшествующем периоде.
ОВ пл.задания 
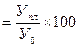
Относительные величины динамики, планового задания и выполнения плана связаны между собой следующим соотношением:
ОВ динамики = ОВ вып.пл. * ОВ пл.задния
4.Относительные величины структуры – характеризуют доли, удельные веса составных элементов в общем итоге (отношение части к целому). Сумма относительных величин структуры всегда равна единице или 100 %. В эту же группу входят характеристики отношения между отдельными частями объекта; показатели, характеризующие степень сложности структуры, степень неравномерности (вариации) долей и др.
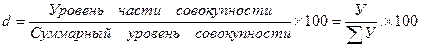 .
.
5.Относительные величины интенсивности – отношение двух разноименных величин. Характеризуют степень распределения или развития данного явления в той или иной среде и представляют собой отношение абсолютного уровня показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком.
Пример. Среднегодовая численность населения региона составила 310,2 тыс. человек. Число родившихся за год - 2918 чел. Определим относительную величину интенсивности, характеризующую рождаемость.
Коэффициент Число родившихся .1000 = 2918 х 1000 = 9,4 ‰
рождаемости = Среднегодовая 310200
численность населения
На каждую 1000 человек населения рождалось 9,4 человек.
6. Относительные величины координации характеризуют отношения частей изучаемой совокупности к одной из них, принятой за базу сравнения. Они показывают, во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1, 10, 100, 1000 единиц другой части. Эти относительные величины могут быть исчислены как по абсолютным показателям, так и по показателям структуры.
Пример. Экономически активное население региона составило 860.4 тыс. человек.
В том числе: занятое в экономике - 780.3
безработные - 80,1
Определим, сколько безработных приходится на 100 занятых в экономике региона.
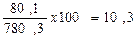 Относительная величина = человека
Относительная величина = человека
координации
7. Относительные величины сравнения – показатели, представляющие собой частные от деления одноименных абсолютных статистических величин, характеризующих разные объекты, относящиеся к одному и тому же периоду (или моменту) времени.
Пример. Товарооборот региона "А" составил 1834,6 млн. руб., а региона "Б" - 4217,5 млн. руб. Исчислим относительную величину сравнения, приняв за базу сравнения товарооборот региона "А".
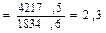 Относительная величина сравнения
Относительная величина сравнения
Следовательно, товарооборот в регионе "Б" в 2,3 раза больше, чем в регионе "А".
Средние величины
Главное значение средних величин состоит в их обобщающей функции, т.е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной совокупности.
Средняя величина – обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна исчисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
Определить среднюю во многих случаях удобнее через исходное соотношение средней (ИСС) или ее логическую формулу:
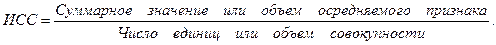
Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение средней. Однако от того, в каком виде представлены исходные данные, зависит, каким именно образом исходное соотношение средней будет реализовано.
Например. Средняя заработная плата равна отношению фонда заработной платы к среднесписочной численности работников.
В экономических исследованиях применяются две категории средних:
· степенные средние;
· структурные средние.
Формулы средних величин могут быть получены на основе степенной средней:
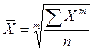 ,
,
где п – число признаков (вариантов) Σf = n;
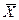 - среднее значение;
- среднее значение;
т – показатель степени;
Х – текущее значение (вариант) осредняемого признака.
Приведем формулы расчета различных видов степенных средних (табл. 1).
Таблица 1
Дата добавления: 2016-02-16; просмотров: 5022;
