jсм, j плотностей соответственнотока смещения, электрическоготока равны по величинеи противоположныпо знаку. Других проекций у векторов этих плотностей тока нет, поэтому векторы

j_см, j плотностей соответственнотока смещения, электрическоготока являются коллинеарными векторамии направлены в противоположныестороны, т.е.векторы j_см, j плотностей соответственнотока смещения, электрическоготока связаны между собой следующим соотношением: j = -j_см.(3.8)

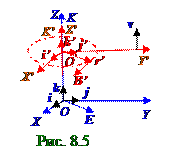
На рис. 8.4 векторы изображены для случая, когда в некоторый момент времени q заряд на внутренней сфере уменьшаетсяво времени, т.е.(рис.6.2) из раздела 6.0 "Электрический ток" внутренняя сфера является "истоком" свободныхзарядов, а dq < 0. Поэтому (3.7) в некоторый момент времени j_r проекцияна направление r радиуса - вектора вектора j плотности электрическоготока имеет численное положительное значение, а этот (рис. 8.4) вектор j плотности электрическоготока коллинеарен r радиусу- векторуи направлен с ним в однусторону. Тогда согласно (3.8) вектор j_см плотности тока смещения(рис. 8.4)и r радиус- векторявляются коллинеарными векторамии направлены в противоположныестороны.

Проекция j_r на направление r радиуса - вектора вектора j плотности электрическоготокас учётом (3.6) имеет следующий вид: j_r = E_r/ρ = D_r/ε₀ερ. (3.9)

Подставляем (3.1) проекцию D_r на направление r радиуса - вектора вектора D электрического смещенияв (3.9) и получаем следующее выражение проекцииj_r на направление r радиуса - вектора вектора j плотности электрическоготока: j_r = q/4πr²ε₀ερ, (3.10)

Согласно (3.8) проекция j_rсм на направление r радиуса - вектора вектора j_см плотноститокасмещения с учётом выражения (3.9) имеет следующий вид: j_rсм = - q/4πr²ε₀ερ, (3.11)

где ρ = 1/σ- удельное сопротивление слабо проводящейсреды между концентрическими металлическими сферами, равноеобратной величинеσудельной проводимостиэтой среды;

ε - диэлектрическая проницаемость среды между концентрическими металлическими сферами; знак

"-" в (3.10) учитывает численное отрицательное значение проекции j_rсм на направление r радиуса - вектора вектора j_см плотноститока смещения в случае (рис.8.4)численного положительного значения q заданного в условии задачи свободного заряда на внутренней сферы в некоторый момент времени; в случае численного отрицательного значения q заданного в условии задачи свободного заряда на внутренней сферы в некоторый момент временипроекция j_rсм на направление r радиуса - вектора вектора j_см плотноститока смещенияимеет положительное значение.

Сила I_см тока смещения сквозь (6.8) из раздела 6.0 "Электрический ток"

с учётом выражения (3.11) и перпендикулярности (рис. 08.1.4)вектора j_см плотноститокасмещения воображаемойзамкнутой поверхность S_r= 4πr² площадью в некоторый момент времени имеет следующий вид: I_см = ∫j_смdS = ∫j_rсмdS = - q/4πr²ε₀ερ ∫dS = - q4πr²/4πr²ε₀ερ=- q/ε₀ερ,(3.12) (S_r) (S_r) (S_r)

где j_rсм = - q/4πr²ε₀ερ -проекция j_rсм на направление r радиуса - вектора вектора j_см плотноститокасмещениявынесенав (3.12) за знак интеграла вследствие того, что эта j_rсм проекция на всей воображаемойзамкнутой поверхности S_r= 4πr² площадью постоянна по величине; знак "-" в (3.12) учитывает противоположное направлениесилы I_см тока смещения r радиусу - векторув случае

(рис.8.4)численного положительного значения q₊ заданного в условии задачи свободного заряда на внутренней сферы в некоторый момент t времени; в случае численного отрицательного значения

q заданного в условии задачи свободного заряда на внутренней сферы в некоторый момент времени сила I_см тока смещенияимеетодинаковое направлениес r радиусом - вектором.

Задача 3

В некоторой области K(x,y,z,t) неподвижнойинерциальной системы отсчёта (ИСО) имеется только электрическое поле, вектор Eнапряжённости которого находится в OXY плоскости и зависит от x, y координат согласноследующему уравнению:E = a(xi + yj)/(x² + y²), где a В - постоянная. Определить выражение вектора B′индукции магнитного поля в K′(x′,y′,z′,t′) подвижной инерциальной системе отсчёта (ИСО), которая с нерелятивистским значением v модуля v вектора скорости перемещается относительно K(x,y,z,t) неподвижной ИСО в направлении OZ оси. Какой графический вид имеет векторное поле B′ индукции магнитного поля в K′(x′,y′,z′,t′) подвижной ИСО?

Дано: E = a(xi + yj)/(x² + y²); v= vk /B′ = ?

где учтено нерелятивистское значение v << c модуля постоянной скорости, с которым K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OZ осиK(x,y,z,t) неподвижнойИСО,вследствиечего (3.25) из раздела 3.0 "Релятивистская механика" релятивистский

β = 1/[1 - (v²/c²)]^1/2 коэффициентпримерноравенединице, т.е. β ≈1.

Векторное произведение (4.1) в(1.1)из раздела 1.0 "Физические основы механики" прямоугольной декартовой системе координат имеет следующий вид:

B′ = - (1/c²)[- i(vay/(x² + y²) + j(vax/(x² + y²)] = - (1/c²)[a/(x² + y²)]( - ivy + jvx) =

= - (1/c²){a/[(x′)² + (y′)²]( - i′v y′ + j′vx′) = - (1/c²){a/[(x′)² + (y′)²][vr′]= [a/(r′)²c²][ r′ v], (4.2) где i =i′, j =j′ - равные вектора, поскольку равны их единичные модули и они имеютодинаковое направление, т.е. векторы параллельны и ориентированы в одну сторону; x=эта K′(x′,y′,z′,t′) подвижнаяИСО, y=y′ - равные координаты соответственно в K(x,y,z,t) неподвижнойИСО и в K′(x′,y′,z′,t′) подвижнойИСО, поскольку эта K′(x′,y′,z′,t′) подвижнаяИСО перемещается относительно K(x,y,z,t) неподвижной ИСО в направлении OZ оси.

Согласно (4.2) вектор B′ индукции магнитного поля в K′(x′,y′,z′,t′) подвижнойИСО перпендикулярен векторуvпостоянной скорости с нерелятивистским значением v модуля, с которымэта K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OZ осиK(x,y,z,t) неподвижнойИСО, а также перпендикулярен r′ радиусу - вектору, направленному в точку пространства K′(x′,y′,z′,t′) подвижнойИСО, в которой определяется вектор B′ индукции магнитного поля.

Согласно (4.2) r′ модуль r′ радиуса - вектора, направленного в точку пространства K′(x′,y′,z′,t′) подвижнойИСО, в которой определяется вектор B′ индукции магнитного поля, связан с

x′, y′ прямоугольными декартовыми координатамив этой K′(x′,y′,z′,t′) подвижнойИСО следующим уравнением окружности: r′ =[ (x′)² + (y′)²]^1/2, (4.3) т.е. вектор B′ индукции магнитного поля в точке пространства K′(x′,y′,z′,t′) подвижнойИСО лежит в

O^'X′Y′ плоскости и направлен по касательной к окружности (4.3) r′ радиуса.

Задача 4

Векторы E′ напряженности электрического и B′ индукции магнитного полей в K′(x′,y′,z′,t′) подвижнойИСОпри (рис. 9.1), (рис. 9.2) из раздела 9.0 "Электромагнитные волны. Излучение" её движении вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО с вектором

vпостоянной скорости связаны с векторами E напряженности электрического и B индукции магнитного полей впроизвольнойM точке пространства неподвижнойИСО с использованием

(9.1) из раздела 9.0 "Электромагнитные волны. Излучение" частных преобразованийЛоренца следующими соотношениями: E_||′ = E_||; B_||′ = B_||; E_┴′ =(E_┴ + [v,B])/[1-(v²/c²)]^1/2; B_┴′ =[B_┴ -([v,E])/c²]/[1-(v²/c²)]^1/2, где E_||′ = E_|| - равныесоставляющие векторов E′, E напряжённости электрическогополя, параллельные векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО; E_┴′,E_┴ -составляющие

векторов E′, E напряжённости электрическогополя, перпендикулярные вектору

vпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО; B_||′ = B_|| - равныесоставляющие векторов

B′, B индукции магнитного поля, параллельные векторуvпостоянной скорости, с которой

K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY оси

K(x,y,z,t) неподвижнойИСО; B_┴′,B_┴ -составляющие векторов B′, B индукции магнитного поля, перпендикулярные векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО.

Убедиться с помощью этих соотношений в инвариантностиследующих выражений: а)EB;

векторов E_┴′, B_┴′;E_||′, B_┴′ и E_┴′, B_||′.

Подставляем в (5.1) соотношения из условия: E_||′ = E_||; B_||′ = B_|| , вследствие чего получаем следующее выражение скалярного произведение векторов E′ напряженности электрического и

B′ индукции магнитного полей в K′(x′,y′,z′,t′) подвижнойИСО: E′∙B′ = E_||′∙B_||′ = E_||∙ B_|| .(5.2)

E∙B = (E_┴+E_||)∙(B_┴+ B_||) = E_||∙ B_||, (5.3) где E_┴∙ B_┴ = 0; E_||∙ B_┴ = 0; E_┴∙ B_|| = 0, вследствие перпендикулярности векторов E_┴, B_┴;E_||, B_┴и E_┴, B_||.

Согласно (5.2), (5.3) скалярное произведение векторов E′ напряженности электрического и

B′ индукции магнитного полей в K′(x′,y′,z′,t′) подвижнойИСО и скалярное произведение векторов

E напряженности электрического и B индукции магнитного полей в K(x,y,z,t) неподвижнойИСО равны друг другу, что свидетельствует обинвариантности EB а) выражения из условия данной задачи, т.е. оно выполняется в любой ИСО.

В неподвижной K(x,y,z,t) ИСО б) выражение из условия данной задачи имеет с учётом

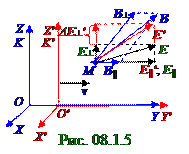
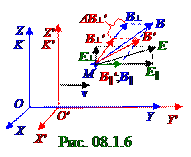
(Рис. 08.1.5, Рис. 08.1.6) E = E_┴ + E _||;B = B_┴ + B_|| следующий вид:

E² - c²B² = (E_┴ + E _|| )∙(E_┴ + E _|| ) - c²(B_┴ + B_||)∙(B_┴ + B_||) = E_┴² - c²B_┴² + E _||²- c²B_||² , (5.4) где E_┴∙E _|| = 0; E_||∙E_┴ = 0; B_||∙B_┴= 0; B_┴∙ B_|| = 0, вследствие перпендикулярности

векторов E_┴, E _|| и B_┴, B_||.

В K′(x′,y′,z′,t′) подвижнойИСО б) выражение из условия данной задачи имеет с учётом

(Рис. 08.1.5, Рис. 08.1.6) E′ = E_┴′ +E_||′_;B′=B_┴′ +B_||′ следующий вид:

E′² - c²B′² = (E_┴′+E_||′)∙(E_┴′+E_||′) - c²(B_┴′ +B_||′)∙(B_┴′ +B_||′) =E_┴′² - c²B_┴′² +E_||′² - c²B_||′², (5.5)

где E_||′∙E_┴′= 0; E_┴′∙E_||′= 0; B_||′∙B_┴′ = 0; B_┴′∙B_||′= 0, вследствие перпендикулярности

векторов E_┴′, E_||′и B_┴′, B_||′.

Подставляем в (5.5) выражения E_||′ = E_||; B_||′ = B_||; E_┴′ =(E_┴ + [v,B])/[1-(v²/c²)]^1/2;

B_┴′ =[B_┴ -([v,E])/c²]/[1-(v²/c²)]^1/2 из а), б) условий данной задачи, вследствие чего получаем следующее соотношение: E′² - c²B′² = {(E_┴ + [v,B])∙(E_┴ + [v,B])/[1-(v²/c²)]} -

- c²{(B_┴ - [v,E] /c²)∙(B_┴ - [v,E] /c²)/[1-(v²/c²)]} + E_||² - c²B_||². (5.6)

Подставляем в (5.6) выражение B = B_┴ + B_||; E = E_┴ + E_||, где B_┴, B_|| и E_┴, E_|| -составляющие векторов соответственно B индукции и E напряженности магнитногои электрического

полей впроизвольнойM точке пространства неподвижной K(x,y,z,t) ИСО соответственно перпендикулярные и параллельные векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО, и получаем следующее выражение: E′² - c²B′² = {(E_┴ + [v,(B_┴ + B_||)])∙(E_┴+[v,(B_┴ + B_||)])/[1-(v²/c²)]} -

- c²{(B_┴ - [v,(E_┴ + E_|| ) ]/c²)∙(B_┴ - [v,(E_┴ + E_|| )]/c²)/[1-(v²/c²)]} + E_||² - c²B_||² = {(E_┴ + [v,B_┴] +[v,B_||])∙(E_┴ +

+ [v,B_┴] +[v, B_||])]/[1-(v²/c²)]}- c²{(B_┴ - [v, E_┴/c²]- [v, E_||/c²])∙(B_┴ - [v, E_┴/c²]-[v, E_||/c²])/[1-(v²/c²)]}+E_||² -

- c²B_||²= {(E_┴ + [v,B_┴])∙(E_┴ + [v,B_┴])/[1-(v²/c²)]} - c²{(B_┴ - [v, E_┴]/c²)∙(B_┴ - [v, E_┴]/c²)/[1-(v²/c²)]} + E_||² -

- c²B_||² = {(E_┴²+ [v,B_┴]∙E_┴ + E_┴∙[v,B_┴])+ [v,B_┴]∙[v,B_┴]/[1-(v²/c²)]} - c² {(B_┴²- [v, E_┴]B_┴/c² - B_┴[v, E_┴]/c²+

+ [v, E_┴]∙[v, E_┴]/ c⁴)/[1-(v²/c²)]} + E_||² - c²B_||² ={(E_┴² + [v,B_┴][v,B_┴] /[1-(v²/c²)]} - c²{(B_┴²+

+[v, E_┴]∙[v, E_┴]/c⁴)/[1-(v²/c²)]} + E_||² - c²B_||² = {(E_┴²+ v²B_┴²)/[1-(v²/c²)]} - {(c²B_┴²+v²E_┴²/c²)/[1-(v²/c²)]} +

+ E_||² - c²B_||² = [E_┴²+ v²B_┴² - c²B_┴²-(v²E_┴²/c²])]/[1-(v²/c²)]}+ E_||² - c²B_||² = {E_┴²[1 - (v²/c²)] - c²B_┴²[1 - (v²/c²)]}/[1-(v²/c²)]}+ E_||² - c²B_||² = E_┴² - c²B_┴² + E _||²- c²B_||² , (5.7)

где при выводе (5.7) учтено, что [v, B_||] = 0, [v, E_||/c²] = 0, вследствие параллельности (Рис. 08.1.5, Рис. 08.1.6) векторов соответственно vи B_||, v и E_||, а также учтено, что[v,B_┴]∙E_┴= 0, E_┴∙[v,B_┴] = 0 и [v, E_┴]B_┴/c² = 0, B_┴[v, E_┴] = 0, вследствиеперпендикулярности векторов соответственно [v,B_┴] и E_┴, [v, E_┴] и B_┴/c².

Вследствие равенства (5.4), (5.7) E² - c²B² б)выражение из условия данной задачи является инвариантом, т.е. оно выполняется в любой ИСО.