Электромагнитная индукция, энергия магнитного поля

Занятие 5. Движение заряженных частиц в магнитных и электрических полях.

Электромагнитная индукция, энергия магнитного поля

Вариант 7

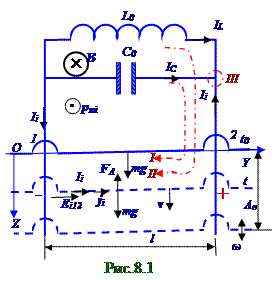
пересекающий контур:1-2 перемычка l длиной, катушка L₀ индуктивностис включённымпараллельно конденсаторомC₀ ёмкостью, увеличивается, поэтому dФ_m/dt > 0. Вектор p_mi магнитного момента(рис. 8.1) индукционного тока I_iсилой (рис.8.2) из раздела 8.0 "Электромагнитная индукция.УравненияМаксвелладля электромагнитного поля" согласно правилу Ленца коллинеарен вектору Bиндукциивнешнего магнитного поля и направлен в противоположнуюемусторону.Вектор p_mi магнитного момента индукционного тока I_iсилой направлен перпендикулярно чертежу и на наблюдателя, поэтому этот индукционный(рис.8.1) токI_i силойи ЭДС индукции Ε_i12 (8.6)из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля " в 1-2 перемычке направлены против часовой стрелки по правилу "правого винта".

Вследствие перпендикулярностивектора v скорости движения 1-2 перемычки l длинойвектору Bиндукциивнешнего магнитного поля ЭДС индукции(8.6)из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" в 1-2 перемычкеимеет следующее значение без учёта знака, поскольку направление этой ЭДС индукции Ε_i12 значением определено на рис.8.1 согласно правилу Ленца: Ε_i12 = Bvl. (1.1) Направим ток I_L, I_C силой (рис.8.1) соответственно через катушку L₀ индуктивности и конденсатор C₀ емкостью по " часовой стрелке". ЭДС самоиндукцииΕ_L значением (8.13) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" на катушке L₀ индуктивности и (6.39) из раздела 6.0 "Электрический ток" U_C напряжение на конденсаторе C₀ емкостьюв произвольныймомент t времени имеет следующий вид: t Ε_L = - L₀ (dI_L /dt); U_C = q/C₀ ↔ dU_C/dt = (1/C₀)dq/dt ↔ dU_C/dt = (1/C₀)I_C ↔ U_C = (1/C₀)∫I_Cdt.(1.2)

0 С учётом ЭДС индукции Ε_i12 значением (1.1) в 1-2 перемычки l длиной, принимающее отрицательноезначение, т.к. направлениеэтойЭДС индукции Ε_i12 противоположно направлениюобходов I и II контуров, с учётом (1.2) ЭДС самоиндукцииΕ_L значением и U_C напряжения на конденсаторе C₀ емкостьюв произвольныймомент t времениIIзаконКирхгофадля этих I и II контуров (рис.8.1)с обходом их по " часовой стрелке" принимает следующий вид: t

(I): - Ε_i12 = U_C ↔ Bvl = - (1/C₀)∫I_Cdt ↔ dv/dt = - I_C/BlC₀ ↔ I_C = - BlC₀ (d²z/dt²). (1.3) 0 (II): - Ε_i12 + Ε_L = 0 ↔ Bvl =- L₀ dI_L /dt ↔ I_L = - (Bl/L₀) ∫vdt ↔ I_L = - Blz/L₀ . (1.4)

0

С учётом входящихв III узел токов I_i, I_C (1.3) и I_L (1.4) силой соответственноиндукционного, через конденсатор C₀ емкостьюи катушку L₀ индуктивности, а также с учётом равенства нулю выходящихиз III узла токовI законКирхгофадля этого III узла принимает следующий вид:

(III): I_i + I_C + I_L = 0 ↔ I_i = BlC₀ (d²z/dt²) + Blz/L₀ (1.5) Вектор F_Асилы Ампера, приложенной к 1-2 перемычке l длиной,с учётом(7.75) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" силы dF_ААмпера, действующей на 1-2 перемычку с силой индукционным токомI_i силойи малойdl длиной, а также с учётом определения вектора dl (7.1) из раздела 7.1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях"малой1-2 перемычки l длиной, имеет следующий вид: 2 22 2 F_А = ∫dF_А= I_i∫[dl,B] = I_i∫[(j_i/j_i),B] dl = I_i [(j_i /j_i),B] ∫ dl = I_i[(j_i /j_i, B]l,(1.6) 1 1 1 1

где j_i- вектор (рис. 8.1) плотности индукционного токаI_i силой, имеющий неизменное направление в сторону этого индукционного тока I_i по прямой1-2 перемычке l длиной; j_i /j_i - единичныйвектор, коллинеарныйвектору j_i (рис.8.1) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля " плотности индукционного токаI_i силой и направленный по прямой1-2 перемычке l длиной в сторону этогоиндукционного токаI_i силой.

С учётом противоположногонаправления вектора F_Асилы АмпераOZ оси, а также с учётом перпендикулярности j_i /j_iединичноговекторавектору Bиндукциивнешнего магнитного поля, вследствие чего векторное произведение(1.6) [(j_i /j_i),B] есть вектор, направленный в противоположнуюOZ оси сторону и имеющий модуль, равный модулю B вектора Bиндукциивнешнего магнитного поля, проекция II законаНьютонана OZ осьдля движения1-2 перемычки

m массой имеет следующий вид: OZ: m(d²z/dt²) = F_АZ + mg = - I_iBl + mg. (1.7) Подставляем выражение индукционного тока I_i из (1.5) в (1.7) и после тождественныхпреобразований получаем следующее дифференциальное неоднородное линейноеуравнение 2 - го порядка: (d²z/dt²) + [B² l²/L₀ (m + B² l²C₀)]z = mg/(m + B²l²C₀). (1.8) Общее z₁(t) решениедифференциального(1.8)однородного линейногоуравнения 2 - го порядкасовпадает со следующим решением дифференциального однородного линейногоуравнения 2 - го порядкадля гармонических(2.7) из раздела 2.0 "Колебания и волны"колебанийпружинного маятника: z₁(t) =Acos(ω₀ t+ φ₀), (1.9) где ω₀ = [B² l²/L₀ (m + B²l²C₀)]^1/2, 1/с - циклическаячастота гармонических колебаний 1-2 перемычки по двум гладким медным шинам; A; φ₀ - соответственно амплитудаи начальная фазаэтих колебаний.

Частноеz₂(t) решениедифференциального(1.8) неоднородного линейногоуравнения 2 - го порядкасовпадает с решением дифференциального неоднородного линейногоуравнения 2 - го порядкадля гармонических(2.61) из раздела 2.0 "Колебания и волны"установившихся вынужденных колебанийи с учетом равенства нулю Ωциклической частотывнешней периодическойсилы, а также равенства нулю β коэффициентзатуханияколебаний 1-2 перемычки по двум гладким медным шинамимеет следующий вид: z₂(t) = A_вcos(Ω t+ φ₀), (1.10) где A_в = mg/[(m + B²l²C₀) (cosΩ t)][(ω₀² - Ω²)² + 4β² Ω²]^1/2 = mg/(m + B²l²C₀)ω₀² =

= mgL₀(m + B²l²C₀)/(m + B²l²C₀)B²l² = mgL₀/B²l²; tgφ₀ = - 2βΩ/(ω₀² - Ω²) ^↔ φ₀ = 0 - соответственно амплитуда A_ви φ₀ в z₂(t) частном (1.10) при Ω= 0 и β =0решениидифференциального(1.8) неоднородного линейногоуравнения 2 - го порядка. Вследствие этого z₂(t) частное (1.10) решение принимает следующий вид: z₂(t) = A_в ^↔ z₂(t) = mgL₀/B²l²,(1.11) т.е. z₂(t) частное (1.11) решениедифференциального(1.8) неоднородного линейногоуравнения 2 - го порядкапредставляет собой (рис.8.1) статическое смещение1-2 перемычки относительно нулякоординат по OZ оси под действием вектора mg силытяжести.

Общее z(t) решениеравно следующей сумме общего (1.9) z₁(t) и частного(1.11) z₂(t) решенийдифференциального(1.8) неоднородного линейногоуравнения 2 - го порядка:

z(t) = z₁(t) + z₂(t) = Acos(ωt+ φ₀) + A_в = Acos(ωt+ φ₀) + mgL₀/B²l².(1.12) Уравнение зависимостипроекции dz/dt скорости 1-2 перемычки по OZ оси от t временис учётом (1.12) имеет следующий вид: dz/dt = -Aωsin(ωt+ φ₀). (1.13) В начальный момент t₀ времени, т.е. при t₀ = 0, z₀ координата и dz/dt|_{t0 = 0} скорость

1-2 перемычки равны нулю.

Согласно (2.5) из раздела 2.0 "Колебания и волны" постоянные величины

A и φ₀ соответственно амплитудыи начальной фаза гармонических колебаний определяются из начальных условий при t₀ = 0, вследствие чего с учётом (1.12), (1.13) для этих начальных амплитуды и фазыколебаний имеют место следующие выражения:

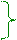
z₀ = Acosφ₀ + mgL₀/B²l² 0 = Acosφ₀ + mgL₀/B²l² ↔ φ₀ = π ↔ A = mgL₀/B²l². (1.14)

v_0Z = (dz/dt) _{t0 = 0} = - Aωsinφ₀ ↔ 0 = - Aωsinφ₀ С учётом (1.13) A и φ₀ соответственно амплитудыи начальной фаза гармонических колебаний уравнения z(t) координаты и dz/dt скорости колебаний 1-2 перемычки по OZ оси имеют следующий вид: z(t) = mgL₀/B²l²[cos(ωt + π) + 1] ↔ z(t) = mgL₀/B²l²(1 - cosωt).

dz/dt = -(ωmgL₀/B²l²) sin(ωt+ π) ↔ dz/dt = (ωmgL₀/B²l²) sinωt.(1.15)

Таким образом, (рис. 08.1.1) перемычка1-2 совершает гармоническиеколебанияс (1.9) циклическойω₀ = [B²l²/L₀ (m + B² l²C₀)]^1/2, 1/с частотой относительно (1.12) статического

A_в= mgL₀/B²l², м смещения по OZ оси c (1.14) A = mgL₀/B²l² амплитудой, равной этому статическомуA_всмещению.

Задача 1

Согласно уравнению Максвелла(8.82) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" в интегральном виде, которое называется законом полного тока, циркуляция вектора H напряжённости магнитного поля по (рис.8.2) контуру l длиной равна при отсутствии тока проводимости первой производнойпоtвремениот N_D потока вектора D электрического смещениячерез поверхностьS площадью, которую ограничивает этот контур l длиной, вследствие чего для этой циркуляции вектора H напряжённости магнитного поля имеет место следующее выражение: ∫Hdl = ∂N_D/∂t = (∂/∂t)∫DdS. (2.1) l S

ПоверхностьS площадью представляет собой сферическую поверхность шаровогосегмента, в основании которого находится круг (рис.8.2) с a радиусом. На окружности a радиуса находится рассматриваемая в задаче A точка, которая одновременно находится на сферической поверхности R радиусом и центром в O начале координат, где начальный момент t₀ = 0 времени находится точечный q заряд.

Электростатическое поле, создаваемое точечным q зарядом (рис.5.8) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" будетсферическимвекторным полем. Вектор D электрического смещения электростатического поля (5.87) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" в вакууме в любой точке проходит через центр сферы, а проекция D _r на направление радиуса - вектора R, направленного из O начала координат, где в данный момент t времени находится точечный q заряд, в рассматриваемую на сферической поверхности шаровогосегмента точку постоянна по величине и знаку. Поэтому проекция D _r вектора

D электрического смещения электростатического поля от точечного q заряда (рис.8.2) на сферической поверхности R радиусом согласно теореме Гаусса(5.89) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" имеет следующий вид:∫DdS = ∫D _rdS = q ↔ D _r4πR² = q↔D _r= q/4πR², (2.2) S₀ S₀

где S₀ = 4πR² - площадь поверхности сферы R радиусом, которая охватывает точечный q заряд.

Поток dN_D вектора D электрического смещения электростатического поля через элементарную поверхность dS площадью (рис.8.2) шарового пояса с учётом значения (2.2) проекции D _r вектора D электрического смещения электростатического поля от точечного q заряда имеет следующий вид: dN_D = DdS = D _rdS = (q/4πR²)2πR(sinα′)Rdα′ = (q/2)(sinα′)dα′, (2.3)

где dr = Rdα′ - ширина шарового пояса с элементарной поверхностью dS площадью; r = R(sinα′) - радиус шарового пояса с элементарной поверхностью dS площадью; α′ - уголшарового пояса относительно OY оси, значение которого изменяется от 0 до α.

Поток dN_D вектора D электрического смещения электростатического поля через элементарную поверхность dS площадью (рис.8.2) шарового пояса является элементомN_D потока вектора D электрического смещения электростатического поля на поверхностиS площадью шаровогосегмента, поэтому этот N_D потокимеет следующий вид: α α

N_D = ∫DdS = ∫D _rdS = (q/2)∫(sinα′)dα′ = - (q/2)cosα′| = (q/2)(1 - cosα), (2.4)

S S 0 0

где α - угол шаровогосегмента относительно OY оси; S - площадь поверхности шаровогосегмента.

Первая производнаяпоtвремениот N_D потока (2.4) вектора D электрического смещениячерез поверхностьS площадьюшаровогосегмента с учётом и правила дифференцирования функцииот функции имеет следующий вид: ∂N_D/∂t = (∂/∂t)∫DdS = (∂/∂t)[(q/2)(1 - cosα)]=(q/2)(sinα)(dα/dt). (2.5) S

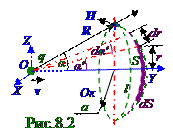
малоеприращение dt времени, когда точечный q заряд переместится по OY оси на элементарное dl перемещение, и R₀ радиусом - вектором, направленным из O начала координат, где в t₀ = 0 начальный момент времени находится этот точечный q заряд. Вследствие малогоdα приращения α угла модули R₀ и R₁ радиусов - векторовравны R величине в (2.6) выражении.

Подставляем (2.6) выражение первой производнойпоtвремениот α угла в (2.5) и получаем следующее выражение первой производнойпоtвремениот N_D потока вектора D электрического смещениячерез (рис.8.3) поверхностьS площадьюшаровогосегмента, как функцию модуля v вектора v скорости перемещение по OY оси точечного q заряда и α угла между R радиусом - вектором, направленным от этого точечного q заряда в A точкунашаровомсегменте, где по условию задачи требуется определить вектор Hнапряжённости магнитного поля: ∂N_D/∂t = (∂/∂t)∫DdS = (q/2)(sinα)vsinα/R=(qv/2R)sin²α, (2.7) S

где R - модуль радиуса - вектора R, направленным от точечного q заряда в A точкунашаровомсегменте, где по условию задачи требуется определить вектор Hнапряжённости магнитного поля.

Циркуляция(2.1) вектора H напряжённости магнитного поля по (рис.8.3) контуру

l длиной, который представляет собой Ок окружность с a радиусом, с учётом направления этоговектора H напряжённости магнитного поля по касательной к контуру l длиной и постоянства

H модулявектора H напряжённости магнитного поля в любой точке этого контура l длиной, имеет следующий вид: ∫Hdl = Н2πa= Н2πRsinα.(2.8) l

Приравниваем (2.8) циркуляцию вектора H напряжённости магнитного поля по (рис. 08.1.3) контуру l длиной(2.7) первой производнойпоtвремениот N_D потока вектора D электрического смещениячерез поверхностьS площадью, которую ограничивает этот контур l длиной, и получаем следующее выражение для модуля Hвектора H напряжённости магнитного поля в любой точке контура l длиной, как функцию модуля v вектора v скорости перемещение по OY оси точечного q заряда и α угла между радиусом - вектором R, направленным от этого точечного q заряда в произвольную A точкуна контуре l длиной:

∫Hdl = ∂N_D/∂t = (∂/∂t)∫DdS ↔ Н2πRsinα = (qv/2R)sin²α ↔ Н = qvRsinα/4πR³. (2.9)

l S

Выражению (2.9) для модуля Hвектора H напряжённости магнитного поля в любой точке контура l длиной соответствует следующее выражение для вектора H напряжённости магнитного поля, как функция векторного произведения вектора v скорости перемещение (рис. 08.1.3) по

OY оси точечного q заряда и R радиуса - вектора, направленного от этого точечного q заряда в произвольную A точкуна этом контуре l длиной:

Н = qvRsinα/4πR³ ↔ Н = q[vR]/4πR³↔ B = μ₀q[vR]/4πR³,(2.10)

где B = μ₀Н - связь в вакууме (7.95) из раздела 7.2 " Магнитное поле в веществе" вектора H напряжённостимагнитного поля с вектором B магнитной индукции в произвольной точке пространства.

Выражение (2.10) полностью соответствует выражению (7.7) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" вектора B_q магнитной индукции в данной M точке, возбуждаемого в вакуумеэлектрически заряженной частицейс q зарядом, которая движется с постоянным вектором v скорости, малой по сравнению со скоростью света (v << с).

Задача 2

Пространство между двумя концентрическими металлическими сферами заполнено слабо проводящейсредой с ρ удельным сопротивлением и ε диэлектрической проницаемостью. В некоторый момент времени заряд на внутренней сфере равен q₊ . Найти: а) связь между векторами плотностейтоков j проводимостии j_смсмещения; б) силу I_см токасмещенияв этот некоторый момент времени через произвольную поверхность в слабо проводящейсреде, охватывающую внутреннюю сферу. Дано: ρ; ε; q /j = f(j_см) = ? I_см= ?

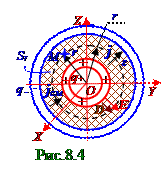
"Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"в этом электрическом поле проходят через центр концентрических металлических сфер, а проекции E_r, D_r на направление r радиуса - вектора векторов соответственноE напряжённости, D электрического смещенияэтого электрическогополя, являющееся сферическимвекторным полем, является функцией r расстояния от центра сферы. Поток N_Dвектора D электрического смещения через воображаемую сферическую(рис.8.4) поверхность

S_r площадью, согласно (5.118) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"имеет следующий вид: N_D= ∫DdS= ∫D_ndS = ∫D_rdS = D_r4πr² = q ↔ D_r = q/4πr², (3.1) (S_r) (S_r) (S_r)

где q -заданный в условии задачи свободный заряд внутренней сферы в некоторый момент времени,охватываемый воображаемой сферическойповерхностью S_r = 4πr²площадью.

Согласно уравнению Максвелла(8.77) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" вектор j_см плотноститока смещения связан следующим соотношением с изменяющимся во t времениэлектрическим полемс вектором D электрического смещения: j_см = ∂D/∂t. (3.2) Электрическое поле (рис.8.4) между концентрическими металлическими сферами, заполненное слабо проводящейсредой с ρ удельным сопротивлением и ε диэлектрической проницаемостью, является сферическимвекторным полем, поэтому вектор D электрического смещенияимеет только однупроекцию, отличную от нуля, - это D_r проекция на направление r радиуса - вектора.

Согласно (3.2) проекцияj_rсм на направление r радиуса - вектора вектора j_см плотноститока смещенияимеет следующий вид: j_rсм = ∂D_r/∂t. (3.3) Подставляем (3.1) проекцию D_r на направление r радиуса - вектора вектора D электрического смещенияв (3.3) и получаем следующее выражение проекцииj_rсм на направление r радиуса - вектора вектора j_см плотноститока смещения: j_rсм = (1/4πr²)dq/dt, (3.4) где j_rсм - проекцияна направление r радиуса - вектора вектора j_см плотноститока смещения имеет численное отрицательное значение, если dq < 0, т.е. если (рис.6.2) из раздела 6.0 "Электрический ток" (рис.8.4) внутренняя сфера является "истоком"свободныхзарядов; j_rсм - проекцияна направление r радиуса - вектора вектора j_см плотноститока смещения имеет численное положительное значение, если dq > 0, т.е. если (рис.6.3) из раздела 6.0 "Электрический ток" (рис.8.4) внутренняя сфера является "стоком"свободныхзарядов.

Сила I тока сквозь (рис.6.2), (рис.6.3) из раздела 6.0 "Электрический ток" (рис. 8.4) воображаемуюзамкнутую поверхность S_r площадью в слабо проводящей среде имеет (6.8) из раздела 6.0 "Постоянный электрический ток" следующий вид: I = - dq/dt,(3.5)Согласно (6.19) из раздела 6.0 "Электрический ток" закону Ома для однородного участка цепив дифференциальномвидевектор j плотности электрическоготока связан следующим соотношением свектором E напряжённости электрическогополя:j = σE. (3.6) Электрическое поле (рис.8.4) между концентрическими металлическими сферами, заполненное слабо проводящейсредой с ρ удельным сопротивлением и ε диэлектрической проницаемостью, является сферическимвекторным полем, поэтому вектор E напряжённости электрическогополяимеет только однупроекцию, отличную от нуля, - это E_r проекция на направление r радиуса - вектора. Поскольку согласно (3.6) вектор j плотности электрическоготока коллинеарени направлен в однусторону с вектором E напряжённости электрическогополя, то этотвектор j плотности электрическоготока имеет тожетолько однупроекцию, отличную от нуля, - это j_r проекция на направление r радиуса - вектора,котораяс учётом (3.4) имеет следующий вид:

j_r = I/S_r = I/4πr² = - (1/4πr²)dq/dt,(3.7) где S_r = 4πr² -площадьвоображаемой сферическойповерхности между концентрическими металлическими сферами, охватывающей заданный в условии задачи свободный заряд внутренней сферы в некоторый момент времени; j_r - проекцияна направление r радиуса - вектора j плотности электрическоготока имеет численное положительное значение, если dq < 0, т.е. если (рис.6.2) из раздела 6.0 "Постоянный электрический ток" (рис.8.4) внутренняя сфера является "истоком"свободныхзарядов; j_r - проекцияна направление r радиуса - вектора вектора j_см плотности электрическоготока имеет численное отрицательное значение, если dq > 0, т.е. если (рис.6.3) из раздела 6.0 "Постоянный электрический ток" (рис.8.4) внутренняя сфера является "стоком"свободныхзарядов.

Согласно (3.4), (3.7) проекцииj_rсм, j_r на направление r радиуса - вектора векторов