Вектор индукции магнитного поля 1 страница

Магнитноеполе создаётся: а) проводниками с током; б) движущимися электрически заряженными частицами и телами; в) изменяющимися во времени электрическимполем.

Силовой характеристикой магнитного поля служит вектор B магнитной индукции, который вводят однимиз трёх эквивалентныхспособов:

а) исходя из силового действия по закону Лоренцамагнитного поля на движущуюся в нём заряженную частицу - точечный электрический заряд;

б) основываясь на силовом действии по закону Био - Савара - Лапласамагнитного поля на малый элемент проводника с током;

в) исходя из силового действия по закону Амперамагнитного поля на небольшую рамку с током.

Для магнитного поля, так же как для электрического(5.6) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля», справедлив принцип суперпозиции: результирующий вектор B магнитнойиндукции поля произвольной системы проводников с токами или системы отдельных движущихся электрически заряженных частиц, тел равен геометрическойсумме векторов B_i магнитнойиндукции всех малых элементов этих проводников или всех движущихся заряженных частиц, тел.

Закон Био-Савара-Лапласа в вакууме для малого элемента проводника с электрическим постоянным током

ЭлементарныйвекторdB_M магнитной индукции в данной M точке (рис. 7. 1) поля в вакууме малого элемента проводника dl длиной, по которому идёт постоянныйэлектрический токIсилой, удовлетворяет закону Био - Савара - Лапласа, имеющего следующий вид: dB= (μ₀I/4πr³)[dl,r], (7.1) где dl= j dl/j - вектор малого элемента проводника dl длиной, коллинеарный вектору j плотноститока, имеющего j модуль, и направленный с ним в одну сторону; r - радиус-вектор, проведённый из началавектора dl в M точку, в которой определяется магнитная индукция; μ₀ = 4π∙10^-7 Гн/м - магнитнаяпостоянная. Направление элементарного вектораdB_M магнитной индукции определяется по правилу Максвеллаили правилу "буравчика": если ввинчивать "буравчик" с правой резьбойпо направлению вектора j плотноститока в элементе проводника dl длиной, то направление движения рукоятки «буравчика» укажет направление вектора dB_M магнитной индукции в M точке. Поэтому вектор dB_M магнитной индукции в M точке направлен перпендикулярно плоскости чертежа на "наблюдателя", что изображено на рис.7. 1 окружностью с точкой в центре.

Модуль |[dl∙r]| (7.1) векторного произведения с учётом φ угла между векторами r и dl (рис. 7.1) имеет следующий вид: |[dl, r]| = dlrsinφ. (7.2) Длина dl малого элемента проводника определяется из прямоугольного (рис.7. 1) треугольника, гипотенузой которого является этот dl малый элемент проводника, а dr являетсякатетом, поскольку он перпендикулярен к r радиусу-вектору, проведённому из началавектора dl в M точку, в которой определяется магнитная индукция, вследствие чего для длины dl малого элемента проводника имеет место следующее выражение:

dl = dr/sinφ = rdφ/sinφ, (7.3) где r -модуль r радиуса - вектора, проведённого из началавектора dl в M точку, в которой определяется магнитная индукция; dφ - элементарныйугол между r радиусом - вектороми прямой, проведённой из концавектора dl в M точку, в которой определяется магнитная индукция; φ -угол междувектором dl и r радиусом - вектором,равным φ углу, противолежащему dr катету в прямоугольном (рис.7. 1) треугольнике.

Подставляем (7.3) в (7.2) и получаем следующее выражение модуля |[dl,r]| векторного [dl,r] произведения (рис. 7. 1) векторов dlи r радиус-вектора: |[dl,r]| = r²dφ. (7.4) Подставляем (7.4) в (7.1) и получаем следующее выражение модуля dB_M вектора dB_M индукции магнитного поля в данной M точкевакуума малого элемента проводника dl длиной:

dB_M = μ₀Idφ/4πr. (7.5) Согласно принципу суперпозициирезультирующий вектор B_M магнитнойиндукции в данной M точке от проводника c током I силой и l длиной, равняется следующему интегралу от векторовdB_M индукции магнитного поля в данной M точкевакуума от малых элементовэтого проводника

dl длиной: B_M = ∫dB_M= (μ₀I/4π) ∫[dl,r]/r³,(7.6)

l l

где r - радиус-вектор, проведённый из началавектора dl в M точку, в которой определяется индукция магнитного поля. Интегрирование в (7.6) проводится по всей l длине проводника.

Закон Био-Савара- Лапласа в вакууме для движущейся с постоянным вектором скорости электрически заряженной частицы

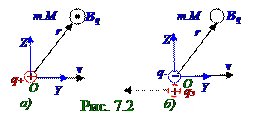
Магнитное поле проводника с током является результатом наложения магнитных полей всехдвижущихся в проводнике электрически заряженных частиц.Вектор B_q магнитной индукции в данной M точке, возбуждаемый в вакуумеэлектрически заряженной частицейс q зарядом, которая движется с постоянным вектором v скорости, малой по сравнению со скоростью света (v << с), имеет следующий вид: B_q = (μ₀I/4πr³)[dl, r] = (μ₀/4πr³)[Idl,r] = (μ₀/4πr³)[(dq/dt)dl,r] = = (μ₀/4πr³)q[(dl/dt, r] =(μ₀q/4πr³)[v, r] ↔ B_q= (μ₀q/4πr³)[vrsin(vˆr)], (7.7) где I = dq/dt - токIсилойравен количеству q заряда, прошедшего через поперечное сечение проводниказа единицу t времени; dq = q - элементарный заряд от одной частицыс q зарядом; v = dl/dt -модуль v скорости вектора v скоростиэлектрически заряженной частицей, имеющей за элементарный dt промежуток времени элементарный dlперемещение; dl= j dl/j - вектор малого элемента проводника dl длиной, коллинеарный вектору j плотноститока, имеющего j модуль, и направленного с ним в одну сторону; r - радиус-вектор, проведённый в произвольный момент t времени от движущейся с постоянной вектором v скоростиэлектрически заряженной частицыв данную M точку, в которой определяется магнитная индукция. Вектор B_q магнитной индукции в данной M точке, возбуждаемый в вакуумеэлектрически заряженной частицейс q зарядом, которая движется с постоянным вектором v скорости, перпендикулярен плоскости, проведённой через векторы v и r. Если q₊>0 (рис.7.2, а), то из конца вектора B_q магнитной индукции в данной M точке, направленного на"наблюдателя", вращение по кратчайшему пути вектора v скорости электрически заряженной частицы к r радиусу - вектору этой частицы видно против часовой стрелки, т.е. в положительномнаправлении. Если q_-< 0

(рис. 7.2, б), то вектор B_q магнитной индукции в данной M точке направлен от наблюдателя, т.к.

направление этоговектора B_q магнитной индукции определяется движением q_э эквивалентного

q_э = |q_-| заряда в направлении вектора v_э скорости, противоположномнаправлению вектору v скорости движения отрицательногоq_- заряда.

Модуль B_q вектора B_q магнитной индукции в данной (рис. 7. 2) M точкесогласно (7.7) переменен во t времени, т.к.радиус-вектор r, направленный от электрически заряженной частицыс q зарядом, движущейся с постоянным вектором v скорости, изменяется по модулюи направлению

Принцип суперпозиции магнитных полей и его применение к расчету в вакууме поля прямого постоянного тока

Длинарадиус-вектора r_м, направленного (рис.7. 3) из началавектора dl в данную M точку с учётом r₀ расстояния между1-2 прямолинейным проводником, по которому протекает ток Iсилой, и этой M точкой, а также с учётом угла φ между векторамиdlи r, имеет следующий вид:

r_м = r₀/sinφ.(7.8)

Модуль B_Mвектора B_M магнитной индукции поля в вакууме 1-2 прямолинейногопроводника, по которому протекает ток Iсилой,в произвольной M точке c учётом (7.5), (7.8) и φ₁, φ₂ соответственно начальногои конечногоуглов между вектором j плотности тока и радиусами - векторами r_м1, r_м2, проведёнными в данную M точку из начала 1 и конца 2 прямолинейного проводника, имеет следующий вид: φ₂φ₂φ₂ B_M = ∫dB_M = (μ₀I/4π)∫dφ/r_м = (μ₀I/4πr₀)∫sinφdφ = φ₁ φ₁ φ₁ ₌(μ₀I/4πr₀)(cosφ₁- cosφ₂). (7.9)

Принцип суперпозиции магнитных полей и его применение к расчету в вакууме поля кругового постоянного тока

По проводнику, имеющему форму (рис.7. 4) окружностис R радиусом,протекает ток Iсилой. Длина dl малого элемента проводника имеет следующее значение: dl = Rdφ,(7.10) где dφ - центральныйугол сектора, хордой которого является малый dlэлемент проводника, имеющего форму окружностис R радиусом. Радиус-вектор r_M, направленный из начала dlвектора, т.е. А точки, в данную M точку, находящейся на оси виткапроводника с h расстоянием от его плоскости, имеет α=π/2 угол с dl = j dl/j вектором малого элемента проводника dl длиной, коллинеарным вектору j плотноститока, имеющего j модуль, и направленным с ним в одну сторону. Модуль |[dl∙r_M]| векторного произведения с учётом (рис.7. 4) α = π/2 угла между dl и r_M векторами, а также с учётом (7.10) имеет следующий вид: |[dl,r_M]| = r_Mdl = Rr_Mdφ, (7.11)

где r_M - модуль r_Mрадиуса-вектора, направленного из начала dl вектора, т.е. А точки, в данную M точку. Подставляем (7.11) в выражение (7.1), которое переведено в dB = (μ₀I/4πr³)|[dl∙r_M]| форму модуля, и получаем следующее выражение модуля dB_M вектора dB_M магнитной индукции поля в вакууме в данной M точке: dB_M = μ₀IRdφ/4πr_M². (7.12)

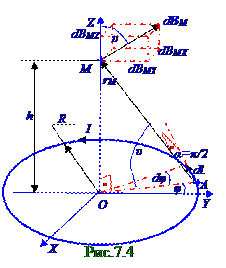
ВекторdB_M магнитной индукции(рис.7.4) перпендикулярен плоскости, проведённой через векторы dl и r_M, и имеет проекции dB_MX, dB_MY и dB_MZ на соответствующие оси декартовойсистемы

координат.

Угол υ между векторомdB_M магнитной индукциии OZосьюравен υ углу между AM гипотенузойr_M= (R² + h²)^1/2 длиной и OAкатетом, равным R, в прямоугольномOMA треугольнике, поэтому имеет следующий вид: cosυ = R/r_M = R/(R² + h²)^1/2.(7.13) Проекция dB_MZ на OZ ось вектораdB_Mмагнитной индукции с учётом (7.12), (7.13) и

r_M² = R² + h²имеет следующий вид: dB_MZ = dB_M cosυ = μ₀IR²dφ/4π(R² + h²)^3/2.(7.14) Проекция B_MZ на OZ ось вектора B_M магнитной индукции в данной M точке, находящейся на оси виткапроводника с h расстояниемот его плоскости, от всех малых элементов проводника dl длиной определится следующим интегрированием (7.14) по φ углу от φ₁= 0 до φ₂= 2π с независимойинтегрирования dφ элементарнымуглом между R радиусамипроводника, проведёнными из начала и концавектора dl малого элемента виткапроводника: 2π 2π B_MZ= ∫dB_MZ = [μ₀IR² /4π(R² + h²)^3/2]∫ dφ = 0 0

= μ₀IR² /2(R² + h²)^3/2. (7.15)

Аналогичные (7.15) проекции B_MX и B_MY на OX, OY оси вектора B_M магнитной индукции в произвольной M точке при интегрировании будут равны нулю, т.к. каждому элементу проводника dl длиной, находящемуся, например, справа от OX оси и имеющему поэтому положительную величину dB_MY проекции, будет соответствовать вследствие симметриидиаметрально противоположный элемент проводника dl длиной, находящейся слева от OX осии имеющий поэтому отрицательнуювеличину dB_MY проекции. Поэтому вектор B_M магнитной индукции в вакууме в данной M точке, находящейся на оси виткапроводника с h расстояниемот его плоскости, будет направлен по OZ оси и его модуль B_M будет определяться (7.15) выражением.

Магнитный поток вектораиндукции магнитного поля в вакууме. Знак и величина магнитного потока

Поток вектора B индукции магнитного поля сквозь элементарную (рис.7.5) воображаемую поверхность dS площадью или dФ_m магнитный потокс учётом единичного n нормального вектора к этой элементарной поверхности dS площадью, поэтому dS = ndS, и проекции B_n вектора B индукции магнитного поля на направление n нормалиимеет следующий вид: dФ_m = BdS = B_ndS = BdScos(Bˆn). (7.16) Элементарная воображаемаяповерхность dS площадью выбирается так, чтобы её можно было считать плоской, а значение вектора B индукции магнитного

поля всюду в её пределах одинаковым.

Магнитный Ф_m поток через всю поверхность S площадью имеет следующий вид:

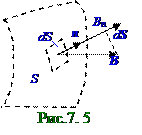
Ф_m = ∫BdS= ∫B_ndS.(7.17) S S При вычислении (7.17) единичный n нормальныйвектор к элементарной (рис.7. 5) воображаемойповерхности dS площадью нужно направлять в одну и ту же сторону по отношению к воображаемой поверхности S площадью. Если магнитное поле однородно, т.е. векторB индукции магнитного поля направленпод одним и тем же углом к воображаемой поверхности S площадью, что выполняется приплоской воображаемой поверхности S площадью, и модуль во всех координатах рассматриваемой поверхностиодинаков, то магнитный Ф_m поток вектораB индукции магнитного поля через всю эту поверхность Sплощадьюимеет следующий вид: Ф_m = B_nS = BScos(Bˆn), (7.18) гдемагнитный поток Ф_m > 0, если векторB индукции однородного магнитного поля ориентирован в однусторонус единичным n нормальнымвектору к плоской воображаемой поверхности

S площадью, т.е. угол 0 < (Bˆn)<π/2; магнитный поток Ф_m < 0, если векторB индукции однородного магнитного поля ориентирован в противоположнуюсторонус единичным n нормальнымвектором к плоской воображаемой поверхности S площадью, т.е. угол π/2 < (Bˆn)< π.

Теорема Гаусса для вектора индукции магнитного поля в вакууме в интегральной и дифференциальной формах

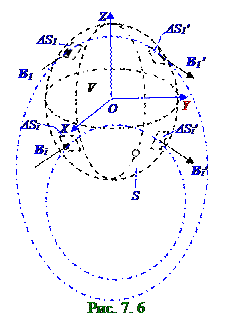
Входящий(рис.7. 6)магнитный (7.18) поток Ф₁ = B_n₁ΔS₁ в вакууме, имеющийв пределах малой воображаемойповерхности ΔS₁ площадьювекторB₁ магнитной индукции поля, вследствие неразрывностилиний магнитного поля, которые на рис.7. 6 изображены штрих - пунктирнымисиними линиями, равен по модулю и противоположен по знаку выходящемумагнитному Ф₁' = B₁'ΔS_i ' потоку, имеющемув пределах малой воображаемойповерхности ΔS₁ площадьювекторB₁' магнитной индукции поля. Суммирование Ф_iвходящихи Ф_iвыходящихпотоков, где i - номер площадки, в пределах которой векторB_i индукции магнитного поля постоянен, приведёт к выводу, чтообщий Ф_m₀ магнитный поток через воображаемую замкнутуюповерхность S площадью, ограничивающую

V объём в вакууме, равен нулю, вследствие чего для этого общего Ф_m₀ магнитного потока имеет место следующее выражение: Ф_m₀ = ∫BdS= ∫B_ndS = 0, (7.19) (S) (S)

что является математическимвыражением теоремы Гауссав интегральномвиде для вектора

B индукции магнитного поля. Теорема (7.19) Гаусса в интегральномвиде является

результатомтого, что в природе нетмагнитныхзарядов, которые являлись бы источниками вектораB индукции магнитногополя. Поэтому линии магнитногополявсегдазамкнуты в отличие от силовых линий электростатическогополя (рис.5.2), (рис.5.3) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля», которые начинаются на положительныхи заканчиваются на отрицательныхзарядах и могут также уходить в бесконечность, если электростатическийзаряд одиночный.

Заменив в (7.17) по аналогии (5.21) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» поверхностныйинтеграл по замкнутой поверхностиS площадью объёмнымпо V объёму, который охватывает эта замкнутая поверхностьS площадью,получим следующее выражение теоремы Гауссав дифференциальномвиде для вектора B индукции магнитного поля: Ф_m0 = ∫BdS= ∫ BdV = 0 ↔ B = 0 ↔ (S) V ↔ (∂B_x/∂x) + (∂B_y/∂y) + (∂B_z/∂z) = 0. (7.20) Согласно (7.20) магнитное полеобладает тем свойством, что его дивергенция B или divB всюду равна нулю, что является математическим выражением теоремы Гауссав дифференциальнойформе для вектора B индукции магнитного поля. Согласно (7.20) численное значение суммы приращений проекцийна каждую из осей декартовойсистемы координат вектора B магнитной индукции поля в вакуумена единицу длины равна

нулю, что является следствием непрерывностии замкнутостилинийиндукциимагнитного поля.

Теорема о циркуляции вектора индукции магнитного поля в вакууме в интегральной и дифференциальной формах

Прямолинейный проводник (рис. 7. 7) с током Iсилойперпендикулярен плоскости чертежа и в случае направления вектора j плотности тока от "наблюдателя", т.е. за чертёж, согласно правилу Максвеллаили правилу "буравчика" векторB_M индукции магнитного поля в данной M точке, находящейся на l контуре, находится в плоскости чертежа и перпендикулярен вектору r_M, направленному от проводника в данную M точку.

Модуль B_M вектораB_M магнитной индукции поля в вакууме от прямолинейного бесконечногоAB проводника, по которому протекает ток Iсилой,в данной M точке c учётом

(рис.7. 3) φ₁ = 0 и φ₂ = π по (7.9) имеет следующий вид: B_M = (μ₀I/2πr_M ),(7.21) где r_M - длина или модуль вектора r_M, направленного от проводника в данную M точку, находящуюся на l контуре.

Дата добавления: 2016-02-14; просмотров: 1308;