Pm магнитного момента-e электрона и B индукции магнитного поля в магнетике.

За dt элементарное приращение t времени от, например, момента (рис.7.34) t₃ = 3T/4 времени элементарное приращение центрального dυ угла окружности имеет с учётом (7.162) следующую величину, которая определяется длиной хорды, т.е. величиной модуля dL элементарного приращения вектораорбитального(7.158) L механического момента:

dυ = dL/Lsinυ ↔ dυ = p_mBsinυdt/Lsinυ ↔ dυ/dt = ω_л = p_mB/L, (7.163) где ω_л - циклическая(1.19)из раздела 1.0 "Физические основы механики" частота вращения векторов орбитальных(рис.7. 34) соответственно (7.158) L механическогои (7.157)

p_mмагнитного моментоввокругвектора B индукциимагнитного поля в магнетике, к которому эти векторы орбитальныхсоответственно L механическогои p_mмагнитного моментов направлены под υ углом, называют ларморовой частотой.

Подставляем (7.157) p_m = evr/2 модуль вектора p_m орбитального магнитного момента

и (7.158) L = rmv модуль вектора орбитального L механического момента -e электрона в (7.163) и получим следующее выражение ω_л ларморовой частоты:

ω_л = p_mB/L ↔ ω_л = (evr/2)B/rmv ↔ ω_л = eB/2m, (7.164) где ω_л ларморова частотане зависит от υ угла, под которым направлены (рис.7.34) векторы орбитальныхсоответственно (7.158) L механическогои (7.157) p_mмагнитного моментовотносительно вектора B индукциимагнитного поля в магнетике, не зависит от r радиуса и vмодуля вектора vскорости вращения-e электрона по окружности и, следовательно, при данном значении B модуля вектора B индукциимагнитного поля в магнетике для всех -e электронов, входящих в состав атома и имеющих e, m соответственноэлементарныйзаряд, массу электрона, эта ω_л ларморова частота постоянна.

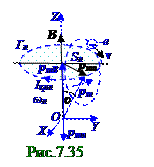
Вращение вектора (7.157) p_mорбитального магнитного момента,направленногопод

υ углом относительно вектора B индукциимагнитного поля в магнетике, можно представить

(рис. 7. 35) суммой двух следующих векторов: p_mB - неподвижного инаправленного по вектору

B индукциимагнитного поля в магнетике; p_mп - подвижного и вращающегося с(7.164)

ω_л циклической(1.19)из раздела 1.0 "Физические основы механики" частотой вращения

"против часовой стрелки".

Наличиеподвижного и вращающегося вектора p_mп орбитального магнитного момента можно объяснить дополнительным вращением -e электрона с(7.164) ларморовой ω_л циклической частотой вращения(рис.7.35) "против часовой стрелки", что эквивалентно протеканию круговоготока"по часовой стрелке" I_крл следующей силы: I_крл = en_л ↔ I_крл = eω_л/2π, (7.165)где n_л = ω_л/2π - число оборотовв единицу времени или ларморова частота вращения -e электрона "против часовой стрелки".

Наличие (7.165) круговоготока"по часовой стрелке" I_крл силы приводит к появлению в диамагнетике вектора p_mл индуцированного орбитального магнитного момента, вызванного дополнительным вращением -e электронов с(7.164) ларморовой ω_л циклической частотой вращения(рис.7.35) "против часовой стрелки" и поэтому направленного противоположно вектору(7.77)из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях"магнитного p_mмомента плоскогоГ контурас круговымтоком I_кр силы, который создаёт -e электрон (рис.7.18) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях", вращающийся "по часовой стрелке" по окружности r радиусом свектором vскорости.

электрическом и магнитном полях", ограниченной плоскимГ_л контуром со cредним по t времени<r_л ²> = (2/3) r_л ² квадратом радиуса окружности, по которому протекает индуцированный круговойтокI_крл силы; ω_л = eB/2m - ларморова циклическая(7.164) частота вращения векторов орбитальных(рис.7.35) соответственно (7.158) L механическогои (7.157) p_mмагнитного моментоввокругвектора B индукциимагнитного поля в магнетике, к которому эти векторы орбитальныхсоответственно L механическогои p_mмагнитного моментов направлены под υ углом; r_л ² - cреднее значениеквадрата радиуса -e электрона (рис.7.33), вращающегося по окружности свектором vскорости вокруг ядра атома.

Среднее по t временизначение в диамагнетикепроекции <pmлZат> на OZ ось вектора вектора pmлат индуцированного орбитального магнитного момента, вызванного дополнительным вращением всех -e электронов Z количеством с (7.164) ларморовой ωл циклической частотой вращения

(рис.7.35), в атоме диамагнетика имеет с учётом (7.166) имеет следующий вид:

Z Z

<p_mлZ^ат> = ∑<p_mлiZ> = - (e²B/6m)∑ r_лi ², (7.167)

i = 1 i = 1

где r_лi ² - cреднее значениеквадрата радиуса i -го электрона -e общим Z количеством, вращающихся по окружности свектором vскорости вокруг ядра в атоме диамагнетика.