В чем физическая суть возникновения ЭДС индукции?

1. Вспомним, что происходит с проводником, движущимся в однородном поле (рис. 11.32, а).

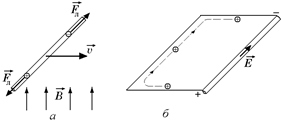Рис. 11.32

На элементарные заряды начинает действовать сила Лоренца, и под действием этой силы заряды разделяются: на одном конце проводника образуется избыток положительных зарядов, а на другом конце – отрицательных (рис. 11.32, б). Из-за этого внутри проводника образуется электрическое поле напряженностью 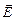, такое, что еЕ = еυВ (электрическая сила уравновешивает силу Лоренца). А во внешней цепи начинается движение зарядов от «плюса» к «минусу» точно так же, как в цепи с обычным гальваническим элементом.

Рис. 11.33

Аналогичная ситуация возникает с вращающейся рамкой (рис. 11.33). На проводниках АВ и СD заряды также разделяются, и возникают как бы два источника тока, соединенные последовательно. Для момента, показанного на рис. 11.33, в точках А и D будет «плюс», а точки В и С – «минус».

Читатель: Получается, что сторонней силой является сила Лоренца? Но ведь сила Лоренца не может совершать работу, так как она всегда направлена перпендикулярно к скорости движения заряда.

Автор: Вы правы. Давайте рассмотрим проводник, движущийся по горизонтальным рельсам со скоростью υ в вертикальном магнитном поле индукции 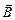(рис. 11.34).

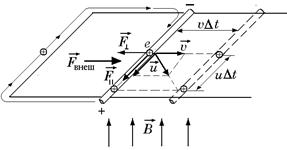
Рис. 11.34

Будем считать, что ток в этом проводнике обусловлен движением элементарного положительного заряда е. На него будет действовать сила Лоренца 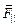, направленная вдоль проводника: F_|| = еυВ. Под действием этой силы заряд будет двигаться с некоторой средней скоростью упорядоченного движения и, и за время Dt пройдет путь Ds₁ = иDt. Тогда сила 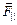совершит работу:

А_|| = F_|| Ds₁ = еυВ× иDt.

Но поскольку заряд движется вдоль проводника со скоростью и, то на него будет действовать сила Лоренца 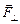, направленная в сторону, противоположную движению проводника: F_^ = еиВ.

(Мы представили движение заряда как сумму движений: вдоль проводника и вместе с проводником, и каждое из этих движений «вызвало к жизни» свою силу Лоренца 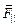и .)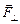

Поскольку заряд вместе с проводником прошел расстояние Ds₂ = υDt, а сила 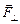направлена в противоположную сторону, то работа этой силы отрицательна:

А_^ = F_^ Ds₂cos180° = еиВ× υDt(–1).

Итак: А_|| = еυВ иDt, А_^ = – еиВυDt.

Как видим, общая работа силы Лоренца

А_|| + А_^ = еυВ иDt – еиВυDt = 0.

В то же время ясно, что для того чтобы проводник двигался вперед с постоянной скоростью υ к нему необходимо приложить внешнюю силу 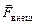, такую, чтобы она полностью компенсировала 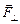: 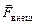= – 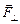. Вот эта сила и является той сторонней силой, которая совершает работу, а сила Лоренца здесь своего рода «передаточный механизм».

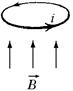Рис. 11.35

2. Совсем другая ситуация, когда индукционный ток возникает из-за изменения магнитного поля. Пусть проводящая рамка находится в переменном магнитном поле (рис. 11.35).

При изменении этого поля в рамке, как мы знаем, возникает индукционный ток, т.е. электроны в рамке приходят в движение.

Но какие же силы заставляют их двигаться? Само магнитное поле, пронизывающее рамку, этого сделать не может, так как магнитное поле действует исключительно на движущиеся заряды (этим-то оно и отличается от электрического), а проводник с находящимися в нем электронами неподвижен.

Что же тогда действует? Кроме магнитного поля, на заряды, причем как на движущиеся, так и на не­подвижные, действует еще поле электрическое, но для тех электрических полей, которые мы рассматривали, необходимо иметь разделенные заряды. А в нашем случае никакого разделения зарядов нет.

Тогда останется единственная возможность: нужно предпо­ложить, что электроны в неподвижном проводнике приво­дятся в движение электрическим полем, и это поле непосред­ственно порождается переменным магнитным полем. Тем самым утверждается новое фундаментальное свойство элек­тромагнитного поля: изменяясь во времени, магнитное поле порождает электрическое поле. К этому выводу впервые при­шел Дж. Максвелл[6].

Теперь явление электромагнитной индукции предстает пе­ред нами в новом свете. Главное в нем – это процесс порожде­ния магнитным полем поля электрического. При этом нали­чие проводящего контура, например катушки, не меняет су­щества дела. Проводник с запасом свободных электронов (или других частиц) лишь помогает обнаружить возникающее электрическое поле. Поле приводит в движение электроны в проводнике и тем самым обнаруживает себя. Сущность явле­ния электромагнитной индукции в неподвижном проводнике состоит не столько в появлении индукционного тока, сколько в возникновении электрического поля, которое приводит в движение электрические заряды.

Вихревое поле

Электрическое поле, возникающее при изменении магнит­ного поля, имеет совсем другую структуру, чем электростати­ческое. Оно не связано непосредственно с электрическими за­рядами, и его линии напряженности не могут на них начи­наться и кончаться. Они вообще нигде не начинаются и не кончаются, а представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Это так называемое вихревое электрическое поле. Может возник­нуть вопрос: а почему, собственно, это поле называется элект­рическим? Ведь оно имеет другое происхождение и другую конфигурацию, чем статическое электрическое поле. Ответ прост: вихревое поле действует на заряд q точно так же, как и электростатическое, а это мы считали и считаем главным свойством поля. Сила, действующая на заряд, по-прежнему равна 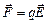,где 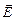– напряженность вихревого поля.

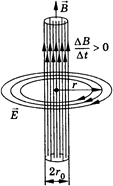Рис. 11.36

Если магнитный поток создается однородным магнитным полем, сконцентрированным в длинной узкой цилиндри­ческой трубке радиусом r₀(рис. 11.36), то из соображений симметрии очевидно, что линии напряженности электрическо­го поля лежат в плоскостях, перпенди­кулярных линиям 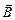,и представляют со­бой окружности. В соответствии с прави­лом Ленца при возрастании магнитной индукции 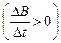линии напряженности 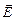образуют левый винт с направлением магнитной индук­ции .

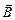В отличие от статического электриче­ского поля работа вихревого поля на замкнутом пути не равна нулю. Ведь при перемещении заряда вдоль замкнутой линии напряженности электрического поля работа на всех участках пути имеет один и тот же знак, так как сила и перемещение совпадают по направлению.

Работа вихревого электрического поля по перемещению единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике.

Вычислим величину напряженности вихревого электрического поля для случая, показанного на рис. 11.36. Поскольку ЭДС – это работа по перемещению единичного положительного заряда, то

|ℰ_i| = E×2pr.

С другой стороны, |ℰ_i| = 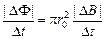, тогда

E×2pr = 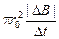Þ

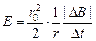. (11.12)

СТОП! Решите самостоятельно: В37, С26, С27, D8.

Бетатрон

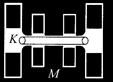Рис. 11.37

При быстром изменении магнитного поля сильного электромагнита появляются мощные вихревые электрические по­ля, которые можно использовать для ускорения электронов до скоростей, близких к скорости света. На этом принципе основано устройство ускори­теля электронов – бетатрона (рис. 11.37). Элект­роны в бетатроне ускоряются вихре­вым электрическим полем внутри кольцевой вакуумной камеры К, поме­щенной в зазоре электромагнита М.

СТОП! Решите самостоятельно: D9.