Вихревое поле и разность потенциалов

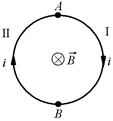Рис. 11.38

Пусть в переменном поле, индукция которого возрастает по линейному закону В = kt, расположено проволочное кольцо, плоскость которого перпендикулярна вектору 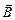(рис. 11.38). При этом за пределами кольца поле отсутствует.

Пусть ЭДС индукции в кольце ℰ_i = const, а длина кольца равна l. Как Вы думаете, чему равна разность потенциалов между точками А и В?

Читатель: Поскольку на участке I ток течет от А к В, то по закону Ома j_А – j_В = iR, где R – сопротивление участка АIВ.

Автор: Да, но на участке II ток течет от В к А, значит, по вашей логике, j_В – j_А = iR, где R – сопротивление участка АIIВ. Получается с одной стороны j_А > j_В, а с другой j_В > j_А.

Читатель: Действительно, что-то тут не так.

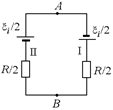Рис. 11.39

Автор: Вы забыли, что мы имеем дело с электрической цепью, содержащей ЭДС, причем в силу того, что эта ЭДС распределена по контуру равномерно, наше кольцо эквивалентно схеме, показанной на рис. 11.39. Ток в этой цепи i = ℰ_i/R.

Рассмотрим участок AIB:

j_В = j_А + ℰ_i/2 – 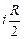= j_А + ℰ_i/2 – (ℰ_i/R) 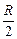= j_А.

Итак, j_В = j_А. Нетрудно доказать, что это верно для любых двух произвольных точек кольца.

Читатель: Значит, если между точками А и В включить вольтметр (рис. 11.40), то он покажет ноль?

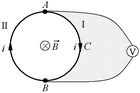Рис. 11.40

Автор: Давайте разберемся. По кольцу идет ток. Часть тока, хотя и ничтожная, может ответвиться и идти через вольтметр (см. рис. 11.40), вызывая отклонение стрелки от нулевого деления. Вспомним, что показание вольтметра опреде­ляется силой проходящего по нему тока; а ток ведь может возникать как за счет кулоновского поля, так и за счет вихревого электрического поля (при наличии ЭДС ток может идти и в отсутствие разности потенциалов). Из-за большого сопротивления вольтметра его подключение практически не приводит к изме­нению силы тока в кольце.

ЭДС индукции ℰ_i равномерно распределена вдоль кольца. Значит, на участке АСВ, составляющем половину кольца, ℰ_АСВ = ℰ_i/2. Рассмотрим теперь заштрихованный контур (см. рис. 11.40). Магнитный поток через него равен нулю, следовательно, полная ЭДС в этом контуре тоже равна нулю. Это означает, что ℰ_АСВ + + ℰ_ВVА = 0, т.е. ℰ_ВVА = –ℰ_АСВ = –ℰ_i/2. Тогда ЭДС на участке АVВ будет равна ℰ_АVВ = –ℰ_ВVА = –(–ℰ_i/2) = +ℰ_i/2. Таким образом, сила тока, проходящего через вольтметр, равна

I_V = [(j_А – j_В) + ℰ_ВVА]/R_V = [0 + ℰ_i/2]/R_V = ℰ_i/2R_V.

И вольтметр показывает U_V = I_VR_V = (ℰ_i/2R_V)R_V = ℰ_i/2.

Читатель: А если кольцо неоднородное? Например, левая половина сделана из проволоки сечением 2S, а правая – сечением S (рис. 11.41). Будет ли в этом случае разность потенциалов между точками А и В равна нулю?

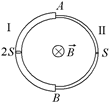Рис. 11.41 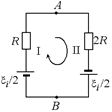Рис. 11.42

Автор: Заметим, что величина ЭДС от этого никак не изменится: ℰ_i = 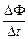, а вот сопротивления участков будут разные. Если считать сопротивление левого участка равным R, то сопротивление правого участка 2R. Ток в кольце будет равен

I = ℰ_i/(2R + R) = ℰ_i/3R.

ЭДС каждого из участков будут одинаковы и равны ℰ_i/2. Заменим кольцо эквивалентной схемой (рис. 11.42) и рассмотрим участок ВIА:

j_А = j_В + ℰ_i/2 – IR = ℰ_i/2 – (ℰ_i/3R)R = ℰ_i/6,

т.е. j_А – j_В = ℰ_i/6 > 0.

СТОП! Решите самостоятельно: В39, С28–С30, D10.