Волновые уравнения для электродинамических потенциалов
Полученные в разделе (3.3) дифференциальные уравнения позволяют в принципе определить векторы напряженности электрического и магнитного поля через функции объемных плотностей сторонних токов и сторонних зарядов. Однако наличие в их правых частях выражений grad ρст и rot jст затрудняет получение удобных расчетных формул. Поэтому, как правило, эти уравнения используют в тех случаях, когда сторонние источники расположены за пределами рассматриваемой области, т.е. когда волновые уравнения становятся однородными.
В общем случае для определения векторов поля по заданным источникам обычно применяют искусственный прием: сначала находят вспомогательные функции, а потом через них вычисляют векторы E и H. Эти вспомогательные функции можно ввести различным образом в зависимости от особенностей решаемой задачи. Для упрощения решения многих задач вводят так называемые электродинамические потенциалы. Из четвертого уравнения Максвелла следует, что ( 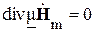 ). Так как дивергенция ротора любого вектора равна нулю (div rot a = 0) то можно утверждать, что
). Так как дивергенция ротора любого вектора равна нулю (div rot a = 0) то можно утверждать, что 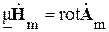 , где Am – комплексная амплитуда некоторого вектора. Представим вектор
, где Am – комплексная амплитуда некоторого вектора. Представим вектор 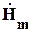 в виде
в виде
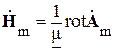
При известном векторе Аm это уравнение позволяет однозначно найти вектор Hm.
Волновое уравнение для векторного потенциала:
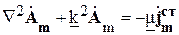 .
.
Векторный и скалярный потенциал связаны соотношением 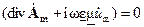 ,
,
которое обычно называют условием калибровки Лоренца
Волновое уравнение для скалярного потенциала:
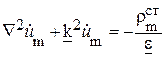 .
.
Дата добавления: 2016-03-27; просмотров: 1939;
