Волновые уравнения для векторов E и H
При решении прямых задач теории электромагнитного поля требуется найти векторы E и H по известным (заданным источникам). Для отыскания этих векторов необходимо решить уравнения Максвелла, что часто бывает весьма затруднительно. Поэтому целесообразно преобразовать систему уравнений Максвелла, исключив либо вектор E, либо вектор H.
Предположим, что сторонние источники расположены в безграничной однородной изотропной среде. Напомним, что однородными называются среды, параметры ε, μ и σ которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Изотропными называются среды с одинаковыми свойствами по разным направлениям.
Для вывода волнового уравнения для комплексной амплитуды вектора 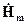 возьмем ротор от правой и левой частей первого уравнения системы
возьмем ротор от правой и левой частей первого уравнения системы
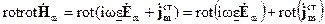 .
.
Учитывая известное из векторного анализа равенство
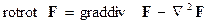
приходим к уравнению
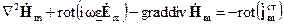
Так как среда однородна и изотропна (ε –не зависит от координат) можно вынести за знак ротора скалярные величины (i, ω и ε), а также принимая во внимание второе и четвертое уравнения Максвелла
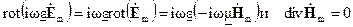
получаем для вектора 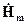 уравнение, называемое векторным неоднородным уравнением Гельмгольца
уравнение, называемое векторным неоднородным уравнением Гельмгольца
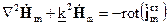 ,
,
где 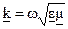 .
.
Для вывода волнового уравнения для комплексной амплитуды напряженности электрического поля 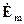 возьмем ротор от второго уравнения Максвелла и проведя элементарные преобразования, получаем уравнение
возьмем ротор от второго уравнения Максвелла и проведя элементарные преобразования, получаем уравнение
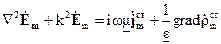
Дата добавления: 2016-03-27; просмотров: 2591;
