Уравнение Бесселя и цилиндрические функции
При рассмотрении электромагнитных полей в областях с симметрией кругового цилиндра встречается обыкновенное дифференциальное уравнение вида
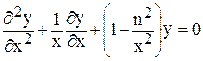 ,
,
которое называется уравнением цилиндрических функций, или уравнением Бесселя n-го порядка. Приведем некоторые сведения о его решениях – цилиндрических функциях.
Тригонометрические и экспоненциальные функции являются решениями дифференциального уравнения
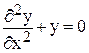 ,
,
которое при некоторых ограничениях можно рассматривать как предельную форму уравнения Бесселя при x → ∞. Сходство этих уравнений помогает понять роль цилиндрических функций в разных задачах, а также их взаимные соотношения. Частным решениям второго уравнения cos x, sin x соответствуют следующие частные решения уравнения Бесселя:
Jn(x) – функция Бесселя n–го порядка,
Nn(x)– функция Неймана n –го порядка.
Точно так же частным решениям eix, e-ix соответствуют частные решения уравнения частные решения уравнения Бесселя:
H(1)n(x) – функция Ханкеля 1-го рода n–го порядка,
H(2)n(x)– функция Неймана 2-го рода n –го порядка.
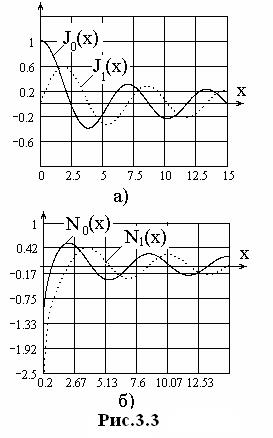
На рис. 8.1 приведены графики некоторых из цилиндрических функций. Подобно тому, как eix=cosx+isinx и e–ix=cosx–isinx, имеют место соотношения
H(1)n(x)= Jn(x) + iNn(x),
H(2)n(x)= Jn(x) – iNn(x).
Цилиндрические функции не являются периодическим (как, например, тригонометрические функции вещественного аргумента), однако это «осциллирующие», колеблющиеся функции. Функции Jn(x) и Nn(x) с возрастанием положительного x принимают значения, колеблющиеся около нуля с монотонно убывающей амплитудой. Их графики создают впечатление деформированных тригонометрических кривых. Полезно помнить, что
 J0(0) = 1, Jn(0) = 0, n ≠ 0
J0(0) = 1, Jn(0) = 0, n ≠ 0
и
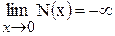
Подобно общим решениям y = A cos x + B sin x и y = Pe–ix + Q eix имеются общие уравнения Бесселя в виде:
y = AJn(x) + BNn(x)
y = PHn(2)(x) + QHn(1)(x).
Обычно требуется, чтобы решение задачи удовлетворяло условию ограниченности y <∞. Соответственно этому, если в рассмотрение входит точка x = 0, то общее решение уравнения Бесселя имеет вид:
y = AJn(x).
Действительно единственная возможность получения ограниченного решения на отрезке, включающем нуль, состоит в том, что неопределенный коэффициент B полагается равным нулю.
Асимптотические представления. При неограниченно возрастающем аргументе Jn(x) и Nn(x) переходят в тригонометрические функции, а Hn(2)(x) и Hn(1)(x) – экспоненциальные
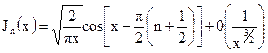 ,
, 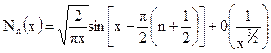 ,
, 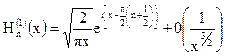 ,
, 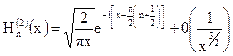 .
.
Употребленный здесь символ 0(...) означает величину, убывающую при x → ∞ как функция, заключенная в скобки (в данном случае 1/x3/2).
Степенные ряды; представления функций малого аргумента. Функции Бесселя представляются степенными рядами вида:
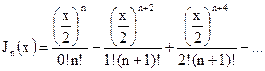 .
.
В частности (учитывая, что 0! = 1),
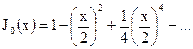
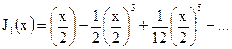 .
.
Поэтому при x << 1
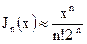 .
.
В частности,
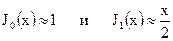 .
.
Ввиду громоздкости ряд для функций Неймана мы не приводим. При x << 1 эти функции представляются в виде:
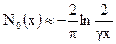 и
и 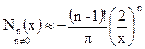 , (γ = 1,781...)
, (γ = 1,781...)
.
Функциональные соотношения. Запишем ряд употребительных формул, используя символ Zn(x) для обозначения произвольной цилиндрической функции (формулы верны при подстановке в качестве Zn(x) функций Бесселя, Неймана и Ханкеля)
Для натурального n
Z–n = (–1)nZn(x).
В частности,
Z–1(x) = –Z1(x).
При дифференцировании цилиндрических функций пользуются соотношениями:
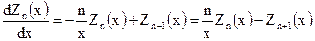
и
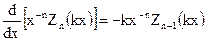
а также
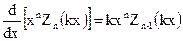
Для n = 0 и n = 1 получаем:
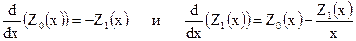
Таблицы корней. Корни уравнения
Jn(x) = 0
это значения аргумента функции Jn(x), при которых она обращается в нуль. Эти числа используются при анализе электромагнитного поля. Обозначая их Bnm, приведем следующую таблицу:
Таблица 3.1
| m n | ||||
| 2,405 | 5,520 | 8,654 | 11,792 | |
| 3,832 | 7,016 | 10,173 | 13,323 | |
| 5,136 | 8,417 | 11,620 | 14,796 | |
| 6,380 | 9,761 | 13,015 | 16,223 | |
| 7,588 | 11,065 | 14,372 | 17,616 |
(n – порядок функции, m – номер корня)
Точно так же важны корни производной функции Бесселя
Jn' (x) = 0
которые обозначены Anm и сведены в таблицу:
Таблица 3.2
| m n | ||||
| 3,832 | 7,016 | 10,173 | 13,324 | |
| 1,841 | 5,331 | 8,536 | 11,706 | |
| 3,054 | 6,706 | 9,969 | 13,170 | |
| 4,201 | 8,015 | 11,346 | ||
| 5,317 | 9,282 | 12,682 |
(n – порядок функции, m – номер корня)
Дата добавления: 2016-03-27; просмотров: 2167;
