Решение однородного уравнения Гельмгольца методом разделения переменных в цилиндрической системе координат

В цилиндрической системе координат (r,φ,z) однородное уравнение Гельмгольца примет вид

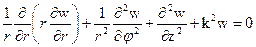
Будем искать решение этого уравнения в виде произведения трех функций

w(r,φ,z) = R(r)^.Φ(φ)^.Z(z),

где R(r) – функция только координаты r, Φ(φ) – функция только координаты φ, Z(z) – функция только координаты z. В результате подстановки в исходное уравнение и деления на w=R^.Φ^.Z получаем:

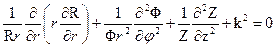
Поступая аналогично случаю решения в декартовой системе координат, получаем систему следующих обыкновенных дифференциальных уравнений, эквивалентную уравнению Гельмгольца:

,

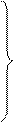
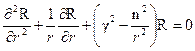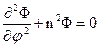, k² = γ²+ γ²_z.

,

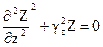Общие решения этих уравнений известны, причем каждое можно записать в двух формах: с использованием функций Бесселя и Неймана или Ханкеля для первого уравнения и с использованием тригонометрических или экспоненциальных – для двух последних уравнений. Таким образом, находим следующее выражение w=R^.Φ^.Z

.

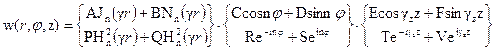Форма записи имеет тот же смысл, что и для декартовой системы; аналогично также значение входящих в выражение постоянных.

[1] Подробно уравнения Максвелла рассматриваются в курсе «Электромагнитные поля и волны».

* Говоря точнее колебания синфазны в каждой области постоянного знака w = 2Pcoskz, а при изменении знака w имеет место скачок фазы на 180⁰