II.7.Характеристические уравнения САР
Рассмотрим замкнутую САР (рис.II.27). Возьмём для определённости САР с единичной отрицательной обратной связью (получение характеристических уравнений для других случаев, например, с неединичной или положительной обратными связями принципиально ничем не отличается от рассмотренного ниже).
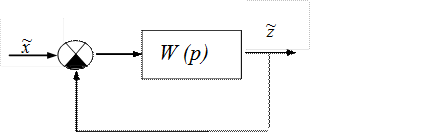
Рис. II.27. Замкнутая САР.
Передаточная функция рассматриваемой системы имеет вид
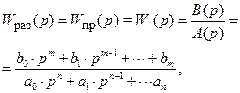 (II.7.1)
(II.7.1)
причём для реальных технических систем n ≥ m. Передаточная функция разомкнутой системы играет весьма большое роль в теории автоматического регулирования, т.к. многие методы анализа и синтеза основаны на использовании именно этой характеристики.
Для замкнутой САР, изображённой на рис.II.27, передаточная функция имеет вид
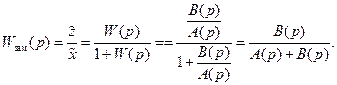 (II.7.2)
(II.7.2)
Полиномы знаменателя (вспомним II.3.3) передаточной функции разомкнутой системы (II.7.1)
А(р) = 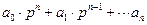
и передаточной функции замкнутой системы (II.7.2)
А(р)+В(р)= = 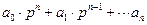 +
+ 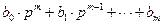 =
= 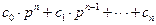
называются характеристическими полиномами. Поскольку n ≥ m, то порядок полинома А(р) + В(р) останется прежним, равным n, т.е. таким же,чтои у А(р), только коэффициенты полинома замкнутой системы ci будут отличаться от коэффициентов разомкнутой системы ai. В дальнейшем характеристический полином любой системы (замкнутой или разомкнутой) будем представлять в виде
D(p) = 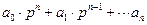 (II.7.3)
(II.7.3)
Например, если 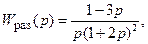 то
то 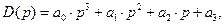 только для разомкнутой системы, поскольку D(p) = A(p) =
только для разомкнутой системы, поскольку D(p) = A(p) = 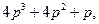 коэффициенты этого уравнения равны, соответственно,
коэффициенты этого уравнения равны, соответственно, 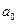 = 4,
= 4, 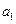 = 4,
= 4, 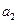 = 1,
= 1, 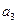 = 0, а для замкнутой системы
= 0, а для замкнутой системы
 А(р)+В(р) =
А(р)+В(р) = 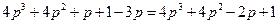
коэффициенты характеристического уравнения примут значения 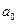 = 4,
= 4, 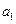 = 4,
= 4, 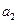 = - 2,
= - 2, 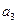 = 1.
= 1.
Приравнивание нулю полинома (II.7.3) даёт характеристическое уравнение системы
D(p) = 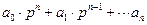 = 0 . (II.7.4)
= 0 . (II.7.4)
Такое название это уравнение получило потому, что оно характеризует, определяет переходный процесс в системе, т.е. динамику САР.
Дата добавления: 2016-04-14; просмотров: 2598;
