II. 9. Поведение САР во временной области
Различают две характеристики, описывающие поведение САР во временной области – переходная функция (характеристика) САР и импульсная переходная (весовая) функция системы.
II. 9.1. Переходная характеристика САР
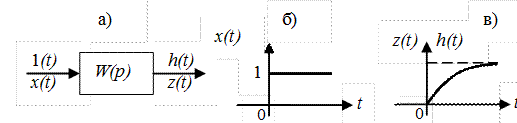
Рис. II. 30. Переходная характеристика САР.
Под переходной характеристикой САР h(t) понимают ее (САР) реакцию на единичный скачок 1(t) (рис. II. 30).
На рис. II. 30,а представлена САР с известной передаточной функцией W(p), на вход которой подается единичный скачок х(t) = 1(t), приведенный на рис. II. 30,б. На выходе появляется сигнал z(t), зависящий от конкретного вида САР, который при единичном входном скачке есть переходная характеристика САР, т.е. z(t) = h(t) (рис. II.30,в).
Характеристику h(t) через известную передаточную функцию системы W(р) можно найти следующим образом.
Известно, что изображения выходной и входной величины связаны соотношением
.
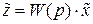В нашем случае изображение выходного сигнала 
, являющегося единичным скачком, согласно [ 7] определяется следующим образом
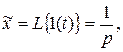
поэтому
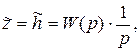
а, значит,
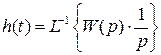, (II.8.1)
т.е. переходная характеристика САР определяется как обратное преобразование Лапласа от произведения передаточной функции САР на изображение единичного скачка. Переходная характеристика является очень мощным инструментом анализа системы, позволяющим оценить многие важные показатели работы САР – устойчивость, быстродействие, перерегулирование, точность и т.п. (см. главы IV и V).
II. 9. 2. Импульсная переходная (весовая) функция систем.
Весовая функция САР w(t) есть ее (САР) реакция на входной единичный
импульс d(t) (рис. II.31).
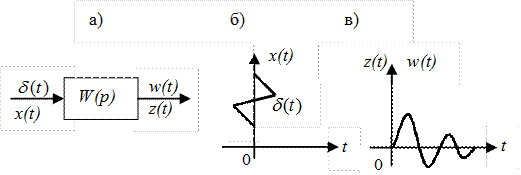
Рис. II. 31. Весовая функция САР.
На вход САР с известной передаточной функцией W(p) (рис. II. 31,а) подается d - функция Дирака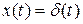 
( рис. II. 31.б). В зависимости от САР на ее выходе появляется определенный сигнал 
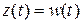( рис. II. 31.в), являющейся по определению весовой функцией. Найти весовую функцию САР можно аналогично вышеизложенному
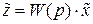
Согласно [ 7] изображение d - функции определяется выражением
,
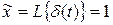тогда
.
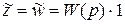Отсюда
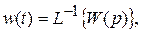(II.8.2)
т.е. весовая функция CАР может быть определена как обратное преобразование Лапласа от передаточной функции САР.
Сравнивая (II.8.1) и (II.8.2) нетрудно понять, что
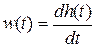. (II.8.3)
Зная весовую функцию САР w(t) для произвольного входного сигнала x(t) можно с помощью интеграла Дюамеля найти выходной сигнал системы z(t)
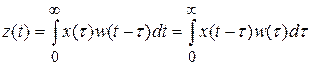. (II. 8.4)
Дата добавления: 2016-04-14; просмотров: 2847;