II.10. Поведение САР в частотной области.

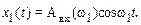Пусть на вход некоторой линейной системы подан гармонический сигнал определений частоты ω₁

На выходе этой линейной системы можно будет наблюдать гармонический сигнал такой же частоты ω₁, но другой амплитуды А _вых (ω₁) и сдвинутый по фазе относительно входного на φ(ω₁)

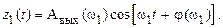
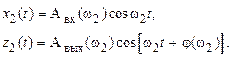Если на вход этой системы подать гармонический сигнал другой частоты ω₂, то выражения для входного и выходного сигналов примут вид

Хотя амплитуды входных сигналов 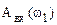, 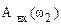и т.д. обычно делают одинаковыми, мы здесь для общности рассматриваем случай, когда они различны и зависят от частоты подаваемого гармонического сигнала.

Вышеприведенные выражения можно записать в общем виде

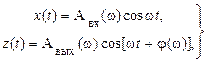(II.9.1)

где частота гармонического сигнала ω может принимать любые вещественные значения.

Воспользуемся формулами Эйлера

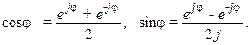
и преобразуем входную и выходную переменные (II.9.1) системы к виду

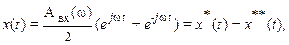
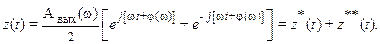
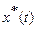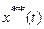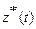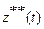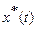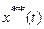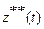В линейной системе на основании принципа суперпозиции можно рассматривать отдельно прохождение составляющих и , которым в выходном сигнале будут соответствовать и . Кроме того, можно легко показать, что достаточно рассмотреть прохождение только составляющей . Оказывается, что соотношение между составляющими и получается таким же, как между 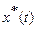и 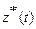. Поэтому в дальнейшем рассмотрении воспользуемся символической записью 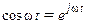. Тогда

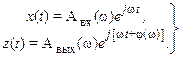(II.9.2)

Символичность этой сокращенной записи заключается в отбрасывании составляющих с множителем .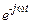

Математическое описание динамических процессов, происходящих в системе автоматического регулирования, или ее математический портрет, могут быть представлены в различной форме. Мы сейчас остановимся на случае, когда динамическая связь между входным x(t) и выходным z(t) сигналами системы задана в виде линейного неоднородного дифференциального уравнения n-ой степени с постоянными коэффициентами

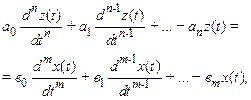(II.9.3)

здесь 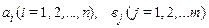– постоянные коэффициенты. Для технически реализуемых систем m ≤ n. Подставив сюда x(t) и z(t) из (II.9.2), получим

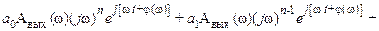
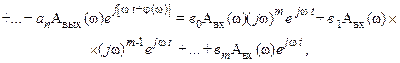
или

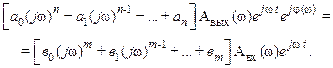
Отсюда после сокращения на общий множитель 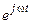найдем

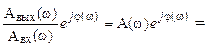
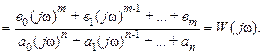(II.9.4).

Данное выражение называется частотной передаточной функцией или комплексным коэффициентом передачи или амплтудно-фазовой характеристиктой системы. Эта и другие характеристики, получающиеся из W(jω), очень важны для анализа и синтеза систем автоматического управления.

Если сравнить это выражение с выражением для передаточной функции системы (II.3.3), то становится ясным, что получение амплитудно-фазовой характеристики (АФХ) системы легко произвести из передаточной функции САР заменой р .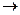

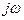Амплитудно-фазовая характеристика, как комплексная функция, может быть представлена в алгебраической, тригонометрической и показательной формах

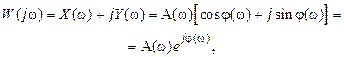(II.9.5)

где Х(ω)и Y(ω)- вещественная и мнимая составляющие W(jω), зависящие от вещественной переменной ω;

А(ω) – модуль W(jω),

φ(ω) – аргумент W(jω).

Зависимости А(ω) и φ(ω) через действительную и мнимую части комплексной функции определяются по известным соотношениям

(II.9.6)

Эти зависимости, характеризующие отдельные свойства АФХ и, следовательно, являющимиеся её составными частями, называются, соответственно:

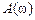- амплитудная частотная характеристика системы (АЧХ). АЧХ-это зависимость от частоты ω, изменяющейся от 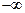до 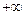, отношения амплитуды выходного гармонического сигнала к амплитуде входного (см. (II.9.4)), или, что то же самое, зависимость от частоты ω, изменяющейся от 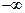до 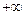, коэффициента усиления САР.

Необходимо отметить, что поскольку частотные характеристики САР симметричны либо относительно действительной или мнимой осей, либо начала координат, то ограничиваются рассмотрением частотных характеристик только для положительного полуинтервала частот от 0 до .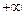

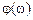- фазовая частотная характеристика (ФЧХ) представляет собой зависимость от частоты ω, изменяющейся от 0 до 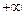,сдвига фаз выходного гармонического сигнала относительно входного.

Построить графические зависимост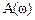и и 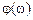можно следующим образом: надо задаться рядом фиксированных значений частоты ω_i в диапазоне от 0 до 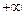, найти для них по формулам (II.9.6) значения 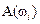и 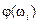, по которым и построить соответствующие графики. Однако вычислять модульА(w) и аргумент j(w) комплексной функцией W(jω) по этим формулам нерационально. Дело в том, что в подавляющем большинстве случаев комплексная функция W(jω) (см. (II.3.3)) представляет собой дробно-рациональное выражение достаточно высокого порядка, поэтому выделять из нее действительную Х(w) и мнимую Y(w) части путем освобождения от мнимости в знаменателе доставляет известные вычислительные сложности. Значительно проще получить нужные результаты другим способом. Известно [7] , что квадрат модуля комплексного числа равен произведению сопряженных комплексных чисел

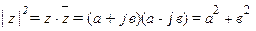
Отсюда нетрудно понять, что для модуля комплексной функции получается

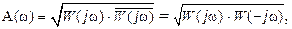(II.9.7)

где W(-jw) – комплексная функция, сопряженная W(jw). Отметим, что для получения W(-jw) надо в W(jw) везде поменять jwна -jw, например:

.

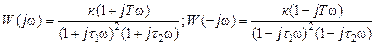Очевидно, что вычисление модуля комплексной функции А(w) по (II.9.7) проще, чем по (II.9.6), т.к. произведение сопряженных комплексных чисел находится практически в уме. Так, для вышеприведенного примера

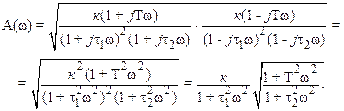
Комплексную функцию W(jw) (II.9.4). являющуюся дробно-рациональным выражением, можно трактовать как частное от деления комплексной функции W_ч(jw), расположенной в числителе, на комплексную функцию W _зн(jw), находящуюся в знаменателе. Пусть для конкретности m = 3 и n = 4, тогда комплексная функция W(jw) (II.9.4) будет иметь вид

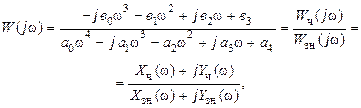
где:

Х _ч(w) = в₃ – в₁w² – действительная часть числителя;

Y _ч(w)=w(в₂ – в₀w²) – мнимая часть числителя;

Х_зн(w)= а₄ – а₂w² + а₀w⁴ – действительная часть знаменателя;

Y _зн (w) =w(a₃ – a₁w²) – мнимая часть знаменателя.

Отсюда получим для комплексной функции W(jw)

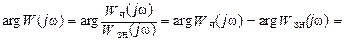
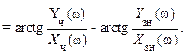(II.9.8).

Видно, что вычисление аргумента комплексной функции W(jω) по этой формуле проще, чем по формуле (II.9.6)., ибо не требует громоздкой операции освобождения от мнимости в знаменателе (II.9.6)..

Остановимся еще на частном случае, когда комплексная функция W(jw) представляет собой дробно-рациональное выражение, числитель и знаменатель которого сами являются произведением комплексных функций, например,

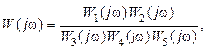
где W_i(jw)обычно задаются в виде 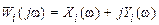(i = 1,…, 5). Учитывая свойства комплексных функций и формулы (II.9.7) и (II.9.8).. , легко найдем

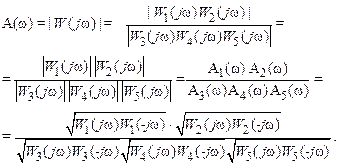
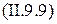
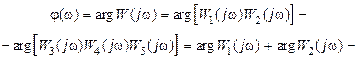
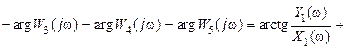
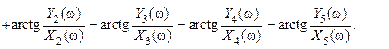
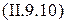
Амплитудно-фазовая характеристика W(jw) САР это совместная зависимость отношения амплитуды выходного сигнала к амплитуде входного и сдвига фаз выходного сигнала относительно входного от частоты, изменяющейся от 0 до .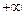

Построение амплитудно-фазовой характеристики возможно двумя способами, первый из которых базируется на алгебраической форме представления комплексной функции 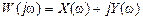, а второй – на показательной форме 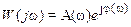. Будем считать, что расчетные значения X(w_i), Y(w_i), A(w_i)и j(w_i) уже известны. Амплитудно-фазовая характеристика W(jw) строится на комплексной плоскости Гаусса. По первому способу для каждой частоты w_i по координатам X(w _i) и Y(w _i) на плоскости Гаусса находится точка 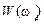(рис. II.31). Полученные точки соединяются затем плавной кривой.

По второму способу для каждой частоты w_i под угломj(w_i) из начала координат проводится луч. Положительное значение угла j(w_i) отсчитывается против часовой стрелки от положительного направления оси абсцисс, а отрицательное значение – по часовой стрелке. Вдоль проведенного луча от начала координат откладывается отрезок прямой с длиной А(w_i) (рис. II.32). Для того, чтобы получить амплитудно-фазовую характеристику, остается только соединить полученные точки плавной кривой.

Нужно заметить, что в ”Теории автоматического управления” много чаще используется второй способ.

Наряду с упомянутыми выше частотными характеристиками – АЧХ, ФЧХ, АФХ – в расчётной практике ТАУ часто встречаются логарифмические амплитудные и фазовые частотные характеристики (ЛАЧХ и ЛФЧХ, соответственно).

Мы уже знаем, что построение АЧХ требует достаточно большой утомительной вычислительной работы. Главным достоинством ЛАЧХ является возможность построения их во многих случаях практически без громоздких вычислений. Это особенно проявляется в тех случаях, когда W(jw) может быть представлена в виде произведения сомножителей. Тогда ЛАЧХ приближенно и очень быстро может быть построена в виде так называемой асимптотической ЛАЧХ, представляющей собой совокупность отрезков прямых линий с наклонами, кратными величинам 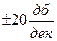. Это будет показано при рассмотрении конкретных звеньев.

Для построения ЛАЧХ определяется функция

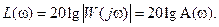
Значения этой функции для текущей переменной 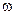выражаются в децибелах (дб). Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один бел соответствует увеличению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т.д. Децибел равен 0.1 части бела.

ЛАЧХ строится в координатах, приведённых на рис.II.33. По оси абсцисс откладывается частота в логарифмическом масштабе. Ось абсцисс разбита по декадам (декада – десятикратное изменение частоты). Внутри декады масштаб логарифмический. По оси ординат откладывается модуль 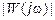в дб. Для этой цели на ней наносится равномерный масштаб. Ось абсцисс должна проходить через точку 0 дб, что соответствует 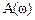= 1 (ибо lg1 = 0). Ось ординат может пересекать ось абсцисс в произвольном месте. Следует учесть,что точка 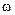= 0 расположена на оси частот слева в бесконечности, т.е. 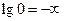.Поэтому ось ординат проводят так, чтобы справа от неё можно было показать весь ход ЛАЧХ. Как будет показано ниже, для этой цели неоходимо провести ось ординат левее самой малой сопрягающей частоты.

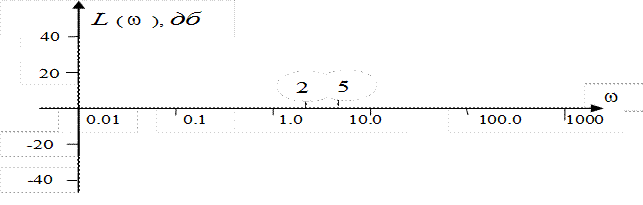
Рис.II.33. Оси и масштаб графика ЛАЧХ.

Логарифмическая фазочастотная характеристика отличается от ФЧХ только тем, что по оси абсцисс в ФЧХ применяется масштаб линейный, а в ЛФЧХ – логарифмический. По оси ординат масштабы у ФЧХ и ЛФЧХ совпадают. ЛФЧХ используется в паре с ЛАЧХ.

Вопросы для самопроверки

1. В чём физический смысл линеаризации нелинейностей?

2. Какие нелинейности называются несущественными?

3.Что такое передаточная функция звена (системы)?

4. Чему равны передаточные функции

а) последовательного соединения звеньев?

б) параллельного соединения звеньев?

в) звеньев, охваченных обратной связью?

5. К чему приводят переносы сумматоров и узлов?

6. Что такое и для чего используются переходная и весовая функции звеньев (систем)?

7. Какие частотные характеристики звеньев (систем) Вы знаете? Дайте их определение.