Анализ уравнения Эйринга
 |
1. а) Как и любая энергия Гиббса, энергия Гиббса активации выражается через энтальпию активации и энтропию активации:
б) Заметим: в результате образования комплекса упорядоченность расположения частиц повышается, так что энтропия снижается.
в) А теплота, в расчете на моль реагирующих частиц, поглощается (поскольку активный комплекс обладает повышенной внутренней энергией).
 |
г) Следовательно, знаки величин таковы:
 |
2.Подстановка (18.42) в формулу Эйринга (18.40) дает:
а) Получается, что температура теперь входит не только в показатель экспоненты (как в уравнении Аррениуса), но и в предэкспоненциальный множитель.
б) И действительно, нагревание оказывает двоякое действие:
- во-первых, по принципу Ле-Шателье, она сдвигает равновесие первой (эндотермической) стадии процесса в сторону образования активированного комплекса,
- во-вторых, ускоряет распад этого комплекса.
 |
в) В итоге получается важное отличие от формулы Аррениуса: при высоких температурах — не стремление k к некоему пределу, а неограниченный рост (рис. 18.8):
3. Какая же зависимость более правильная — по уравнению Аррениуса или по формуле Эйринга?
а) При относительно небольших температурах более точной, видимо, является формула Эйринга.
б) А при высоких температурах она перестает быть справедливой: рост константы скорости ограничивается тем или иным уровнем.
4. Наконец, установим связь величины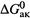 
(или ее компонентов) с энергией активации по Аррениусу (Eак).
 |
а) Для этого выразим константу скорости двумя способами — через уравнение Аррениуса и через формулу Эйринга:
 |
б) Прологарифмируем оба выражения:
в) И, чтобы освободиться от разных констант (А и В), продифференцируем обе части равенства по T:
 |
 |
г) Отсюда и следует искомая связь:
д) Как видно, энергия активации по Аррениусу почти совпадает с энтальпией
(или теплотой) активации.
Таким образом, энергия Гиббса активации — более общее понятие: кроме энтальпии активации, она учитывает и изменение энтропии при активации.
е) Заметим: более точные расчеты показывают, что для бимолекулярной ре-
акции поправка в формуле (18.49) равна не RT, а 2RT.
Краткое содержание главы 18
В главе была рассмотрена ПРИРОДА КОНСТАНТЫ СКОРОСТИ.
1. ТЕОРИЯ АКТИВНЫХ СТОЛКНОВЕНИЙ исходит из следующего.
а) Молекулы вещества различаются по абсолютной скорости, образуя так называемое РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА, из которого вытекает распределение и по КИНЕТИЧЕСКОЙ ЭНЕРГИИ.
б) В реакцию же могут вступать лишь молекулы с энергией выше некоего барьерного уровня (Еб).
в) Разность между этим уровнем и средней энергией молекул вещества – ЭНЕРГИЯ АКТИВАЦИИ по Аррениусу: Еак = Еб – Еср .
г) Доля реакционноактивных молекул с ростом Еакубывает по экспоненте (ЗАКОН БОЛЬЦМАНА).
д) Кроме того, теория учитывает частоту столкновений молекул друг с другом, необходимость их правильной ориентации и ряд других факторов.
 |
е) Это приводит к УРАВНЕНИЮ АРРЕНИУСА:
ж) Согласно ему, с ростом Т константа k растёт тоже, стремясь к предельному уровню А. Причём, если 50 < Eак < 100 кДж /моль, то при увеличении Т на 10 градусов k возрастает в 2–4 раза (ПРАВИЛО ВАНТ-ГОФФА).
 |
з) Логарифмическая форма уравнения описывает линейную зависимость lnk от 1/T. Из неё следует: определив k при двух температурах, можно оценить и Еак , исходя из уравнения:
2. а) В ТЕОРИИ же ЭЙРИНГА считается, что молекулы, обладающие достаточной энергией, образуют вначале АКТИВНЫЙ КОМПЛЕКС.
 |
б) Расчет приводит к ФОРМУЛЕ ЭЙРИНГА:
в) Эта формула описывает БЕСПРЕДЕЛЬНЫЙ рост k при нагревании. Она предпочтительней при не очень больших температурах.
 |
г) Энергии активации двух уравнений связаны соотношением:
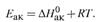
Глава 19. КИНЕТИКА СЛОЖНЫХ ПРОЦЕССОВ
 |
В данной главе будет рассмотрена формальная кинетика сложных процессов, под которыми понимают процессы, содержащие более одной стадии. Вообще говоря, один вид таких процессов мы уже обсуждали в п. 17.2, где речь шла об обратимых реакциях первого порядка
Их можно представить как двустадийные процессы:
 |
Теперь рассмотрим еще несколько видов сложных (в основном, двустадийных) процессов.
Дата добавления: 2016-03-20; просмотров: 2271;