Теория активированного комплекса
Более общей, по сравнению с Еак, является ΔGак – энергия Гиббса активации. Эта величина вводится в рассмотрение во второй теории – теории активированного комплекса, разработанной Эйрингом.
1. Пусть опять речь идет о бисубстратной реакции. Согласно рассматриваемой теории, реакция проходит в две стадии:
 |
а) Первая стадия – обратимая; при этом те молекулы, которые обладают достаточной энергией, образуют активный комплекс.
Энергия данного превращения – это и есть энергия Гиббса активации.
 |
Причём, как и для всякой другой обратимой реакции, стандартное значение этой энергии связано с константой равновесия формулой вида (4.35):
 |
б) Вторая стадия процесса (18.30) – необратимый распад активированного комплекса на продукты; скоростью этого распада и определяется скорость реакции:
2. а) Обычно считается, что скорость второй стадии относительно невелика (по сравнению со скоростями прямой и обратной реакций первой стадии), так что на первой стадии практически успевает установиться равновесие.
 |
б) Тогда можно выразить концентрацию активированного комплекса через концентрации исходных реагентов:
 |
и подстановка в (18.32) даёт:
 |
в) Сопоставление последней формулыс уравнением скорости исходной реакции
 |
приводит к заключению:
Как видно, оно состоит в том, что константа скорости рассматриваемой реакции равна произведению соответствующих констант, характеризующих промежуточные стадии.
3. а) При этом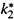 
— это, по сути дела, частота распада возбужденных комплексов с образованием продуктов — в расчете на 1 появляющийся комплекс (тогда это число комплексов, которые при такой частоте распались бы за 1 с), или в расчете на 1 моль комплексов (тогда это количество молей, распавшихся бы за 1 с).
б) Поскольку в комплексе соответствующая связь уже полностью готова к разрыву, она разорвется при первом же колебании, имеющем среднюю для данной температуры энергию. Следовательно,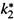 
совпадает с частотой колебаний:
 |
 |
в) Данную частоту можно найти, если считать, что колебательная энергия комплекса равна его потенциальной энергии:
 |
г) Тогда
 |
Здесь фигурируют постоянные Больцмана (kБ) и Планка (h); вспомним их значения:
 |
д)Подставляя их в (18.36, б), можно найти:
е) Отсюдаследует, что образовавшийся комплекс перед превращениемв продукт существует в среднем около
 |
4. а) Подставим выражения для констант
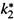(18.36,б) и 
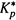(18.31,б) в соотношение (18.34,б). Это дает формулу Эйринга:
б) Она тоже (как и уравнение Аррениуса в предыдущей теории) вскрывает природу константы скорости и устанавливает ее зависимость от температуры.
в) Нетрудно убедиться: с точки зрения размерности эта формула верна лишь
для реакций первого порядка (где [k] = l/с). Для реакций же других порядков
в формулу Эйринга необходимо вводить дополнительный размерный множитель.
Например, в случае реакций второго порядка, где [k] = l/М·с(табл. 16.3), это
 |
множитель l/М:
Дата добавления: 2016-03-20; просмотров: 739;