II. 2. Уравнения звеньев системы. Линеаризация
Математическое описание линейных
Непрерывных систем
II. 1. Постановка задачи
Выше уже говорилось, что, несмотря на все многообразие объектов управления, принадлежащих как технической области, так и областям живой природы и общественных отношений, техника управления, законы управления оказываются общими для всех них. Общий подход к исследованию систем управления такими разнообразными по физической природе объектами оказывается возможным, потому что математическое описание происходящих в них процессов одинаково. Конечно, конкретные инструменты управления такими объектами будут разными, но законы управления – одинаковыми. Отсюда становится понятным, что прежде чем изучать общие законы и технику управления этими многообразными системами, надо научиться получать их математическое описание, т.е. описание процессов, протекающих в системе, на языке математики. Математическое описание может быть аналитическим (с помощью дифференциальных или алгебраических уравнений), графическим и табличным (мы в дальнейшем, как правило, будем использовать аналитические описание).
II. 2. Уравнения звеньев системы. Линеаризация
Вы уже знаете, что САР функционально состоит из отдельных элементов, в качестве которых могут выступать объекты управления, двигатель, редуктор, генератор, усилитель, измерительное устройство и т.п. Первым этапом на пути получения математического описания системы и является выделение ее отдельных элементов и получение их математического описания. В качестве математического описания элемента принимается основной закон, характеризующий протекание динамического процесса в элементе. Так, например, для механических элементов в качестве основного закона берется обычно закон сохранения энергии, для электрических - например, закон Кирхгофа. Элемент системы с его математическим описанием называют звеном. Совокупность уравнений всех элементов дает уравнение САР, или, по другому, математическую модель САР.

Рассмотрим математическое описание непрерывных систем управления с помощью дифференциальных уравнений. Будем считать, что разбиение системы на отдельные элементы и их математическое описание мы уже получили. Отметим, что в большинстве случаев звенья описываются нелинейными дифференциальными уравнениями произвольного порядка.
Для примера рассмотрим частный случай звена (рис. II.1), описываемого нелинейным дифференциальным уравнением второго порядка
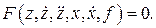 (II.2.1)
(II.2.1)
Здесь F – дифференциальный (в общем случае нелинейный) оператор,
х(t) – входная величина,
z(t) – выходная величина,
f(t) – возмущение (помеха).
В (II. 2. 1) приняты обозначения
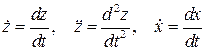
Это уравнение, описывающее процессы в звене при произвольных входных воздействиях x(t) и f(t), называется уравнение динамики звена.
Рассмотрим случай постоянных входных воздействий х = х° = const и f = f° = const. После окончания переходного процесса, когда производные переменных системы станут равными нулю
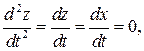
а выходная переменная примет постоянное установившееся значение z°, уравнение (II.2.1) будет выглядеть следующим образом
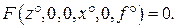 (II.2.2)
(II.2.2)
Это уравнение описывает статический или установившийся режим работы звена и его называют уравнением статики.
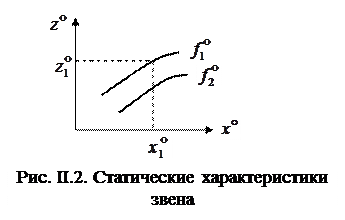
Статический режим можно описать графически с помощью статических характеристик (рис. II.2). Статической характеристикой эвена (а также всей системы) называют зависимость выходной величины от входной в статическом режиме. Ее можно получить теоретически (II.2.2) или экспериментально, подавая на вход звена (системы) постоянные воздействия и измеряя выходные величины после завершения переходного процесса.
Вернемся к нелинейному дифференциальному уравнению (II.2.1). Если удастся решить это уравнение, то найдется переменная z(t), описывающая динамические процессы, происходящие в звене. Однако известно, что в общем случае найти аналитическое решение нелинейного дифференциального уравнения не удается, поэтому надо попытаться его линеаризовать. Под линеаризацией понимается процесс такого преобразования нелинейного уравнения в линейное, чтобы оба они давали приблизительно одинаковые результаты. Во многих случаях это удается сделать.
В САР во время работы должен поддерживаться некоторый заданный («базовый», «номинальный») режим, характеризуемый определенными значениями переменных системы. Но из-за различных возмущающих факторов фактический режим работы системы отличается от базового. В нормально спроектированной и функционирующей САР фактический режим лишь немного отличается от базового и отклонения фактических переменных от базовых невелики. Это позволяет провести линеаризацию, разлагая левую часть уравнения (II.2.1) в ряд Тейлора.
Пусть для нашего конкретного примера базовый режим задан следующими значениями переменных
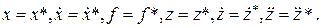 (II.2.3)
(II.2.3)
Тогда в базовом режиме соотношение (II.2.1) примет вид
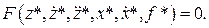 (II.2.4)
(II.2.4)
Обозначим отклонения фактических значений переменных от базовых следующим образом
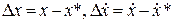 ,
, 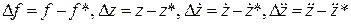 .
.
Перепишем эти соотношения чуть по-другому
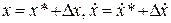 ,
, 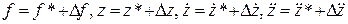 . (II.2.5)
. (II.2.5)
После подстановки этих переменных в (II.2.1) получим
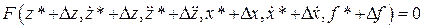 .
.
Левую часть этого уравнения размножим в ряд Тейлора вокруг точки базового режима (II.2.3)

Здесь через О(d) обозначены нелинейные члены разложения в ряд Тейлора (члены второго и более высокого порядка малости), которые будем считать при линеаризации по крайней мере на порядок меньше линейных, и отбросим их. Первый член разложения 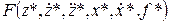 согласно (II.2.4) равен нулю. Поэтому (II.2.6) представим в виде
согласно (II.2.4) равен нулю. Поэтому (II.2.6) представим в виде
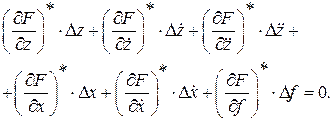
 (II.2.7)
(II.2.7)
Здесь звездочка у скобок означает, что производная вычисляется в точке базового режима и, следовательно, является коэффициентом. В самом деле, пусть F(z)= z3+2z2+4z+1, а точкой базового режима является значение z* =1. Тогда (т.к. здесь всего одна переменная z, то частная производная заменяется полной)
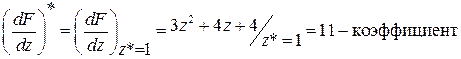 .
.
Введя обозначения
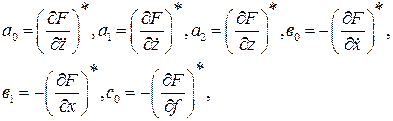
уравнение (II.2.7) преобразуем к виду
 (II.2.8)
(II.2.8)
Таким образом, путем разложения в ряд Тейлора вокруг точки базового режима мы провели линеаризацию: нелинейное дифференциальное уравнение второго порядка (II.2.1) заменили линейным дифференциальным уравнением второго порядка с постоянными коэффициентами (II.2.8) Звенья и системы, которые описываются линейными дифференциальными уравнениями, называются соответственно линейными звеньями или системами.
Линеаризация нелинейностей возможна только для несущественных нелинейностей. Наличие несущественной нелинейности означает, что
а) отклонения фактических переменных от базовых достаточно малы;
б) функция F обладает непрерывными частными производными по всем своим аргументам в окрестности точки базового режима;
в) нелинейные члены разложения функции F в ряд Тейлора по крайней мере на порядок меньше линейных.
Если хотя бы одно из этих требований не выполняется, то линеаризацию проводить нельзя (нелинейность существенна).
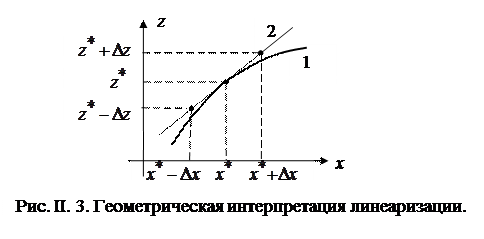
Геометрическая интерпретация линеаризации состоит в том, что статическая характеристика нелинейного звена (кривая 1 на рис. II.3) заменяется касательной к этой кривой в точке базового режима (прямая 2). Видно, что чем меньше отклонение от базового режима Dх, тем ближе кривая 1 и прямая 2, т.е. тем меньше ошибка линеаризации.
Часто по умолчанию в линеаризованном уравнении (II.2.8) значок D
опускают и записывают
 (II.2.9)
(II.2.9)
предполагая, что линеаризация уже произведена и здесь участвуют не сами переменные, а их отклонения от базового режима.
Уравнение (II.2.9) представляет собой частный случай, когда дифференциальное уравнение имеет второй порядок, а на выходной сигнал z влияют только входной сигнал х и его производная по времени 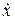 и помеха f. В более же общем случае линеаризованное дифференциальное уравнение звена или САР может быть записано в виде
и помеха f. В более же общем случае линеаризованное дифференциальное уравнение звена или САР может быть записано в виде
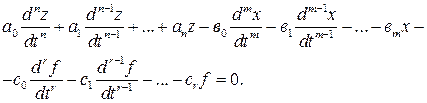
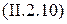
Дата добавления: 2016-04-14; просмотров: 4528;
