II. 3. Преобразование Лапласа в теории управления. Передаточная функция звена (системы)

Применим преобразование Лапласа

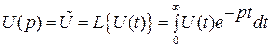
к уравнению (II.2.10):

.

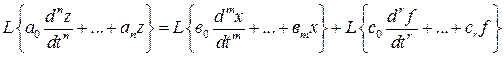Известно, что для линейных стационарных систем дифференциальное уравнение, преобразованное по Лапласу, совпадает с операторной формой дифференциального уравнения. Получить же операторную форму дифференциального уравнения при нулевых начальных условиях можно, если положить 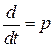. Тогда

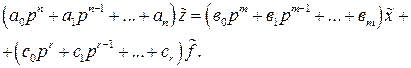(II.3.1)

Соотношение (II.3.1) это дифференциальное уравнение звена (системы) в форме Лапласа (или операторной форме) при нулевых начальных условиях.

Из (II.3.1) видно, что на выходной (управляемый) сигнал 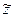влияют как полезный (управляющий) сигнал 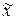, так и помеха 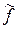. Очевидно, что влияют они на 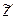, поскольку приложены в разных точках, по-разному, т.к. 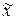входит в (II.3.1) с полиномом 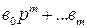, а .

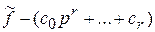Если в (II.3.1) положить 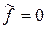, то получится уравнение, связывающее только управляющий (полезный) сигал 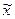и управляемый (выходной) сигнал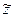

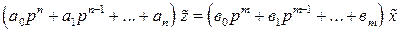(II.3.2)

Введем понятие передаточной функции звена (системы).

Передаточной функцией W(p) звена (системы) называется отношение Лапласовых изображений выходной величины к входной при нулевых начальных условиях.

Поскольку в (II.3.2) входным сигналом является полезный сигнал 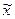, то из этого уравнения передаточная функция по полезному сигналу найдется следующим образом

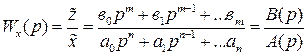(II.3.3)

Для технически реализуемых систем порядок числителя «m» не должен превосходить порядок знаменателя «n».

Нижний индекс х в обозначении передаточной функции W_x(p) указывает на то, что речь идет о передаточной функции по полезному сигналу.

Зная изображение полезного сигнала 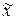и передаточную функцию W_x(p) можно найти из (II.3.3) изображение по Лапласу выходного сигнала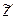

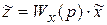
Обратим внимание на то обстоятельство, что передаточную функцию (II.3.3) мы получили как пропорцию из Лапласовой (операторной) формы дифференциального уравнения (II.3.2). Таким образом, дифференциальное уравнение звена и его (звена) передаточная функция связаны между собой однозначно (то же относится и к системе), т.е. по заданному дифференциальному уравнению можно найти передаточную функцию и наоборот.

Положим теперь в уравнении (II.3.6) равным нулю полезный сигнал, т.е. 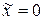. Тогда получим

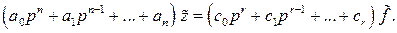
Отсюда найдем передаточную функцию звена (системы) по помехе

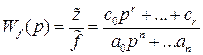(II.3.4)

И отсюда видно, что поскольку точки приложения воздействи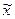й и 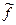в общем случае не совпадают, не совпадают между собой и W_x(p) и W_f(p), отличаясь числителями (знаменатели всегда одинаковы).

Если уравнение (II.3.1) разделить на многочлен 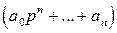, то с учетом (II.3.3) и (II.3.4) получим

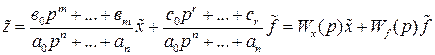
В дальнейшем мы будем иметь дело только с полезными сигналами, а не помехами, поэтому для краткости в выражении W_x(p) нижний индекс будем опускать, обозначая передаточную функцию по полезному сигналу через W(p).

II. 4. Практикум