II. Преобразование комплексных чисел из показательной формы в алгебраическую
1. Точка, соответствующая комплексному числу, расположена в 1-м квадранте ( 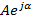 ).
).
А) Вставить движок в линейку обратной стороной (sin, S – T,Tg);
Б) Начало или конец шкалы Tg движка установить над значением модуля по основной шкале линейки;
В) Подвести под низ визира значение аргумента 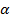 или дополнительного угла
или дополнительного угла 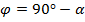 (если
(если 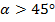 ) на шкале sin движка;
) на шкале sin движка;
Г) Не сдвигая визира, перемещением движка подвести под нить визира значение угла 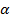 или дополнительного угла
или дополнительного угла 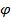 (если
(если 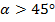 ) на шкале Tg;
) на шкале Tg;
Д) Под началом (или концом) шкалы Tg движка отсчитать составляющую комплексного числа на основной шкале линейки. Вторую составляющую отсчитать по основной шкале под нитью визира. При определении порядка составляющих комплексного числа
необходимо учитывать, что каждая из составляющих должна быть меньше модуля, а сумма составляющих – больше модуля.
Если 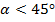 , то a > b; если
, то a > b; если 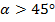 , то b > a
, то b > a
Пример: 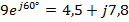
Примечание: а) Если аргумент 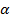 ( или дополнительный угол
( или дополнительный угол 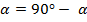 имеет величину в пределах от
имеет величину в пределах от 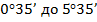 , то нить визира следует установить над углом
, то нить визира следует установить над углом 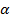 или
или 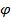 по средней шкале движка (S – T). Отсчет составляющих производиться также под концом шкалы Tg движка и под нитью визира на основной шкале линейки. При этом одна из составляющих будет равна модулю, а вторая меньше модуля в десятки раз.
по средней шкале движка (S – T). Отсчет составляющих производиться также под концом шкалы Tg движка и под нитью визира на основной шкале линейки. При этом одна из составляющих будет равна модулю, а вторая меньше модуля в десятки раз.
б) Если аргумент 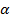 (или дополнительный угол
(или дополнительный угол 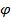 ) имеет величину в пределах от
) имеет величину в пределах от 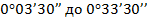 , то этот угол необходимо увеличить в 10 раз и определить составляющие, как указано в п. 1примечания. При этом одна из составляющих будет также равна модулю, а вторая меньше модуля в сотни раз.
, то этот угол необходимо увеличить в 10 раз и определить составляющие, как указано в п. 1примечания. При этом одна из составляющих будет также равна модулю, а вторая меньше модуля в сотни раз.
2. Точка, соответствующая комплексному числу, расположена в IV-м квадранте.
Преобразование комплексного числа производиться порядком, изложенным в предыдущем пункте. Отличие заключается в том, что мнимая часть комплексного числа всегда будет со знаком «минус».
Пример: 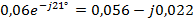
3. Точка, соответствующая комплексному числу, расположена во II-м квадранте, т.е. 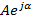 , где
, где 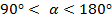 . В рассматриваемом случае комплексное число целесообразно представить в виде:
. В рассматриваемом случае комплексное число целесообразно представить в виде:
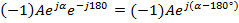
Комплексное число 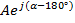 , имеющее аргумент меньше
, имеющее аргумент меньше  со знаком «минус», преобразовать в алгебраическую форму по правилам, изложенным в пункте 1 и 2 и полученный результат умножить на множитель (-1).
со знаком «минус», преобразовать в алгебраическую форму по правилам, изложенным в пункте 1 и 2 и полученный результат умножить на множитель (-1).
Пример:
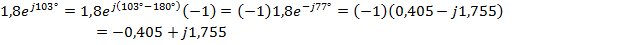
4. Точка, соответствующая комплексному числу, расположена в III-м квадрате комплексной плоскости, т.е. 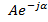 , где
, где 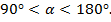
Заданное комплексное число приведем к виду:
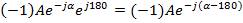
Комплексное число 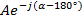 , имеющее аргумент меньше
, имеющее аргумент меньше  со знаком «плюс», преобразовать в алгебраическую форму по правилам, изложенным в п. 1 и полученный результат умножить на множитель (-1).
со знаком «плюс», преобразовать в алгебраическую форму по правилам, изложенным в п. 1 и полученный результат умножить на множитель (-1).
Пример:
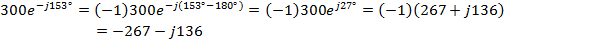
Дата добавления: 2016-04-06; просмотров: 3081;
