Решение однородного уравнения Гельмгольца методом разделения переменных в декартовой системе координат

При решении граничных задач для различных уравнений с частными производными широко используется так называемый метод разделения переменных, позволяющий свести исходную задачу к трем задачам для обыкновенных дифференциальных уравнений. Этот метод применим при использовании ортогональных систем координат (например декартовой, цилиндрической, сферической и др.), когда граничная поверхность задачи может рассматриваться как координатная.

Однородное уравнение Гельмгольца

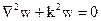
в декартовой системе координат (x,y,z) принимает вид

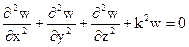
Будем искать решение этого уравнения в виде произведения трех функций

w=w(x.y,z) = X(x)^.Y(y)^.Z(z),

где X(x) – функция только координаты x, Y(y) – функция только координаты y, Z(z) – функция только координаты z. Подставим в исходное уравнение и разделим все члены на w=X^.Y^.Z. Это дает

.

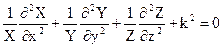Как видно первые три члена – функции разных аргументов, а четвертый постоянен, то есть

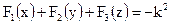
Предположим, что переменные y и z – принимают некоторое фиксированное значение тогда F₂(y) и F₃(z) – становятся некоторыми константами.

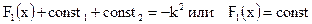
Рассуждая аналогичным образом можно показать что F₂(y) и F₃(z) являются постоянными величинами. Тогда можно записать следующую систему из трех обыкновенных дифференциальных уравнений

.

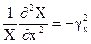
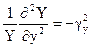
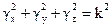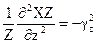
Общие решения таких уравнений хорошо известны:

X(x) = Acosγ_xx + Bsinγ_xx или ,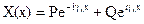

.

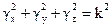Можно записать аналогичные решения и для Y(y) и Z(z). Таким образом, получаем

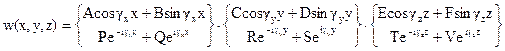Данная символическая запись означает, что каждый из сомножителей решения (X,Y и Z) можно брать как в форме верхней, так и в форме нижней строчки. Очевидно, что записанная функция выражает решение исходного уравнения при любых постоянных коэффициентах A,B,…,T,V и любых постоянных 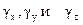, удовлетворяющих равенству в нижней строчке.

Л Е К Ц И Я - 5