Решение однородных волновых уравнений Гельмгольца. Плоские волны

Если в рассматриваемой области отсутствуют сторонние источники, то электромагнитное монохроматическое поле описывается однородными уравнениями для комплексных амплитуд:

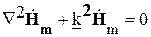
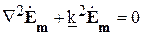
Каждое из векторных уравнений этой системы эквивалентно трем однотипным скалярным уравнениям для координатных составляющих соответствующего вектора:

,

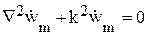где 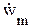– любая из составляющих 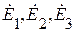или .

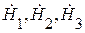Предположим, что в среде отсутствуют потери, следовательно, нужно положить 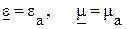и .

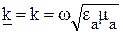Однородное уравнение Гельмгольца в декартовой системе координат (x,y,z) принимает вид

,

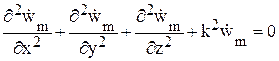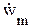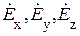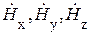где – любая из составляющих или . Предположим, что поле не зависит от координат x и y ( 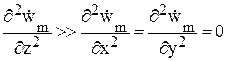). Это справедливо при определении поля в области V, размеры которой малы по сравнению с расстоянием до источника. Тогда имеем обыкновенное дифференциальное уравнение

.

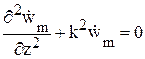Его решение возьмем в форме

.

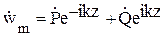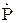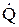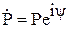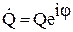Точки над и поставлены, чтобы подчеркнуть, что это в общем случае, произвольные комплексные константы и . Чтобы найти w, возьмем 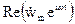; это дает:

w(z,t) = Pcos(ωt – kz + ψ) + Q cos(ωt + kz + φ).

При Q = 0.

w(z,t) = Pcos(ωt – kz + ψ) .

Поверхность, на которой в данный момент времени мгновенное значение функции постоянно, принято называть поверхностью равных фаз(ПРФ). По виду этой поверхности классифицируются волны. Волны, у которых ПРФ – плоскость, называются плоскими.

ПРФ перемещается в пространстве со скоростью:

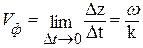
Таким образом имеем плоскую гармоническую волну, движущуюся со скоростью V_ф вдоль оси Z; введенный параметр k называется волновым числом. Значения функции w(z,t) периодически повторяются. Пространственный период называется длиной волны λ. Очевидно, что

w(z + λ,t) = w(z,t).

Поэтому следует, что k ^.λ =2 π, т.е.

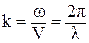, V = λ ^.f,

где f = ω/2π – частота процесса. Заметим, что в данном случае V называется фазовой скоростью. Гармонические волны у которых амплитуда не зависит от поперечных (по отношению к направлению распространения) координат (в рассматриваемом случае x и y) называются однородными

. Л Е К Ц И Я - 4Чтобы составить более наглядное представление о гармонической волне, положим сначала в w(z,t) t =0 и получим

w(z,0) = Pcos(– kz + ψ) = Pcos(kz – ψ),

т.е. функцию, характеризующую распределение величины w вдоль оси Z в начальный момент t = 0. Эта косинусоида (кривая 1 на рис. 5.1) представляет собой как бы «мгновенный снимок» процесса. Выберем следующий фиксированный момент t₁ > 0 и для него запишем:

w(z,t₁) = Pcos(ωt₁ – kz + ψ) = Pcos[k(z – l) – ψ],

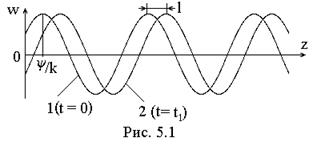
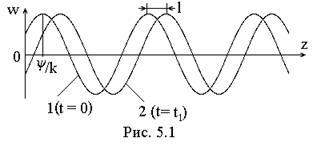где l = ωt₁/V = V^.t₁ – есть не что иное, как расстояние, пройденное волной за время t₁. «Мгновенный снимок», соответствующий моменту t₁, дает, таким образом, косинусоиду, сдвинутую по оси Z на расстояние l (кривая 2 на рис. 5.1).

Распространение гармонической волны – это движение косинусоидального распределения w вдоль прямой (оси Z) с постоянной скоростью (Рис.5.1.). Описываемый процесс называется бегущей волной.

Рассматривая случай P = 0 , получим также плоскую гармоническую волну, но распространяющуюся навстречу оси Z.

Таким образом, найденное решение уравнения выражает суперпозицию двух гармонических волн, распространяющихся со скоростью V в противоположенных направлениях.

Рассмотрим случай бегущих навстречу волн с одинаковыми амплитудами P = Q и начальными фазами ψ = φ . При этом из получаем:

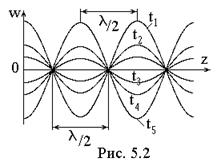
w(z,t) = 2Pcoskz cos(ωt + ψ).

Описываемый процесс называется стоячей волной. Его отличительной особенностью является синфазность колебаний во всем пространстве. Фаза ωt + ψ зависит только от времени и постоянна для всех z; в зависимости от z косинусоидально изменяется амплитуда гармонических колебаний w_m = 2Pcoskz*. Ряд «мгновенных снимков» процесса для разных моментов времени приведен на рис.5.2. Косинусоидальное распределение вдоль оси z не движется (в отличие от бегущей волны), а испытывает синфазные гармонические колебания; при этом расстояния между соседними нулями («узлами») и максимумами («пучностями») распределения равны λ/2.

В случае среды с потерями 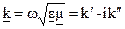, где k' и k" – действительные числа. Соответственно решение уравнения (5.1.3) имеет вид:

,

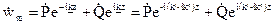или

.

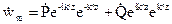Чтобы найти w, возьмем 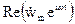; это дает:

w(z,t) = Pe^–k"zcos(ωt – k'z + ψ) + Qe^k"z cos(ωt + k'z + φ).

Гармоническая плоская волна у которой амплитуда зависит только от продольной по отношению к направлению распространения координаты является также однородной:

w(z,t) = w_m(z)cos(ωt – kz).

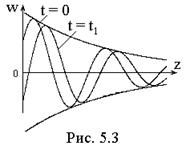
и, в частности, полагая коэффициент Q = 0, получаем гармоническую однородную затухающую волну

w(z,t) = Pe^–k"zcos(ωt – k'z + ψ), (k">0)

с амплитудой, уменьшающейся экспоненциально по мере ее распространения; параметр k" – называется коэффициентом затухания. Два «мгновенных снимка» затухающей волны для моментов t = 0 и t₁ > 0 показаны на рис. 5.3.

Сферическая и цилиндрическая волны выражаются частными решениями однородного уравнения в сферических и цилиндрических координатах при отсутствии зависимости от угловых координат φ и θ в сферической и от φ и z в цилиндрической системах.