Алгоритм метода потенциалов
Пусть имеется матрица перевозок, соответствующая начальному решению хij= 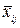 (распределенные ресурсы), xij = 0 для свободных переменных (ресурсы не рас-пределены). Клетки, соответствующие свободным ресурсам, помечены звездочками.
(распределенные ресурсы), xij = 0 для свободных переменных (ресурсы не рас-пределены). Клетки, соответствующие свободным ресурсам, помечены звездочками.
В крайний правый столбец матрицы введем неизвестные ui, а в нижнюю строку – неизвестные vj. Эти n и m неизвестных должны для всех i, j, соответствующих базисным переменным, удовлетворять линейной системе уравнений
ui + vj = cij,(1)
Можно доказать, что эта система для всех базисных решений имеет треугольный вид. Её ранг равен n+m-1, и, следовательно, систему всегда можно решить следующим способом. На первом шаге полагают vn = 0. Если на k-м шаге найдено значение неизвестной, то в системе всегда имеется еще не определенная неизвестная, которая однозначно может быть найдена на (k+1)-м шаге из уравнения (1), так как значение другой неизвестной в этом уравнении уже известно. Это верно до тех пор, пока не найдены все неизвестные. То, какую неизвестную можно найти на (k+1)-м шаге, определяют методом проб. Переменные ui и vj называются потенциалами.
1.Составим и решим систему уравнений (1).
Как было отмечено, уравнения составляются для клеток, в которые распределены ресурсы.
2. Определим расчетные значения затрат zij для клеток, в которые ресурсы не распределены (со свободными переменными):
zij = ui + vj;
3. Вычислим разность заданных и расчетных затрат dij = cij - zij и проверим условие оптимальности dij > 0.
Если все di > 0, то исходный план является оптимальным, и переходят к пункту 5, в противном случае переходят к построению нового плана.
4. Построим новый план (уточним опорный план).
Выберем dab< 0,равное максимальному по модулю dij из состава отрицательных dij, т.е.
dab = - max êdi ê, 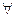 dij > 0.
dij > 0.
Индексом a, bпомечена свободная переменная xab, которая соответствует dab. Соответствующую клетку транспортной таблицы отметим знаком “+”.
Кроме клетки a, bтранспортной таблицы, пометим знаками «–» и «+» другие клетки, в которые ресурсы распределены таким образом, что в каждой строке и столбце транспортной таблицы число знаков «+» будет равно числу знаков «–». Это всегда можно сделать единственным образом, причем в каждой строке и в каждом столбце содержится максимум по одному «+» и «–».
Проставленные в таблице знаки «+» и «–» образуют прямоугольник, в углах которого расположены соответствующие знаки. Указанный прямоугольник далее представляется в виде фрагмента матрицы, который состоит из четырех клеток. В этих клетках производят перераспределение ресурсов (рис. 6).
| b | |||
| - a | + dab<0 | ||
| + | - |
Рис. 6. Фрагмент матрицы
Затем определяем минимум M из всех элементов, помеченных знаками «–», и выбираем одну клетку g,d где этот минимум достигается. При этом g,d обозначает клетку, в которую ресурсы далее распределяться не будут, а все ее содержимое будет распределено между остальными тремя клетками по следующему правилу:
а) в клетку, соседнюю клетке g,d новой таблицы записывается число M;
б) клетка g,d остается пустой;
г) в остальных клетках, помеченных знаками «+» и «–», число M вычитается из стоящего в клетке числа или складывается с ним, в соответствии со знаками;
д) содержимое клеток фрагмента переносится в матрицу, а остальные клетки остаются без изменений;
Таким образом, получили новую матрицу, содержащую новый план.
5. Определим значение целевой функции, с учетом перераспределения в мат-рице (уточнение матрицы проводится до тех пор, пока хотя бы одно значение di <0).
Улучшим опорный план, который был получен ранее.
1. Составим и решим систему уравнений (1).
u1 + v3 = 24 = c13;
u2 + v2 = 18 = c22;
u3 + v1 = 19 = c31;
u3 + v2 = 10 = c32;
u3 + v3 = 100 = c33;
u4 + v1 = 3 = c41;
u4 + v4 = 8 = c44.
Таким образом, имеется семь уравнений и восемь неизвестных, поэтому одному из неизвестных дается произвольное значение, как правило, для облегчения расчетов рекомендуется задаваться нулевым значением. Например u3 = 0, тогда, решая последовательно соответствующие уравнения, получаем v1=19; v2=10; v3=100; v4=24; u1=-76; u2=8; u3=0; u4=-16.
2. Определим значения zij для клеток, в которые ресурсы не распределены.
z11 = u1 + v1 = –76 + 19 = –57;
z12 = u1 + v2 = –76 + 10 = –66;
z14 = u1 + v4 = –76 + 24 = –52;
z21 = u2 + v1 = 8 + 19 = 27;
z23 = u2 + v3 = 8 + 100 = 108;
z24 = u2 + v4 = 8 + 24 = 32;
z34 = u3 + v4 = 0 + 24 = 24;
z42 = u4 + v2 = –16 + 10 = –6;
z43 = u4 + v3 = –16 + 100 = 84.
Определим значения dij и проверим условия оптимальности dαβ> 0
δ11 = с11 – z11 = 70 – (–57) = 127 > 0;
δ12 = с12 – z12 = 38 – (–66) = 104 > 0;
δ14 = с14 – z14 = 92 – (–52) = 144 > 0;
δ23 = с23 – z23 = 56 – 108 = –52 < 0;
δ24 = с24 – z24 = 72 – 32 = 40 > 0;
δ34 = с34 – z34 = 30 – 24 = 6 > 0;
δ42 = с42 – z42 = 36 – (–6) = 42 > 0;
δ43 = с43 – z43 = 121 – 84 = 37 > 0.
Так как d23 < 0, то переходим к формированию нового плана.
3.Построим новый опорный план.
Для его построения строится фрагмент опорного плана (рис. 7) относительно клетки 2, 3 = α, β, т.к. потенциал в ней отрицательный δ23 = δαβ < 0.
| b | b | |||||||||||||
| B2 | B3 | B2 | B3 | |||||||||||
| - a | A2 | * | + d23<0 | - a | A2 | + | ||||||||
| + | A3 | - | + | A3 | * | - | ||||||||
| а | б | |||||||||||||
Рис. 7. Фрагменты плана:
а – фрагмент опорного плана; б – фрагмент нового плана
4. Определим значение целевой функции по новому плану (рис. 8).
| B | a | |||||
| B1 | B2 | B3 | B4 | |||
| A1 | * | * | * | 14 | ||
| A | A2 | * | * | 20 | ||
| A3 | * | * | 26 | |||
| A4 | * | * | 41 | |||
| b | 30 | 22 | 15 | 34 |
Рис. 8. Представление нового плана в форме матрицы
Суммарные затраты по новому плану:
Y1 = 14·24+19·18+1·56+23·19+3·10+7·3+34·8=1494 (усл. ед.).
Прежнее значение суммарных затрат составляло 1546 (усл. ед.).
Рассчитаем процент улучшения опорного плана:
D = 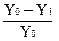 100%=
100%= 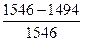 100 % = 3,36 %.
100 % = 3,36 %.
Проведем второй шаг оптимизации.
1. Составим и решим систему уравнений (1)
u1 + v3 = 24 = c13;
u2 + v2 = 18 = c22;
u2 + v3 = 56 = c23;
u3 + v1 = 19 = c31;
u3 + v2 = 10 = c32;
u4 + v1 = 3 = c41;
u4 + v4 = 8 = c44.
При u2 = 0, получим решение v1= 27; v2= 18; v3= 57; v4= 32; u1= –32; u2 = 0; u3 = –8; u4= –24.
2. Определим значения zij для клеток, в которые ресурсы не распределены.
z11 = u1 + v1 = –32 + 27 = –5;
z12 = u1 + v2 = –32 + 18 = –14;
z14 = u1 + v4 = –32 + 32 = 0;
z21 = u2 + v1 = 0 + 27 = 27;
z24 = u2 + v4 = 0 + 32 = 32;
z33 = u3 + v3 = –8 + 56 = 48;
z34 = u3 + v4 = –8 + 32 = 24;
z42 = u4 + v2 = –24 + 18 = –6;
z43 = u4 + v3 = –24 + 56 = 32.
3. Определим значения dij и проверим условие оптимальности dij> 0.
δ11 = с11 – z11 = 70 – (–5) = 75 > 0;
δ12 = с12 – z12 = 38 – (–14) = 52 > 0;
δ14 = с14 – z14 = 92 – 0 = 92 > 0;
δ21 = с21 – z21 = 58 – 27 = 31 > 0;
δ24 = с24 – z24 = 72 – 32 = 40 > 0;
δ33 = с33 – z33 = 100 – 48 = 52 > 0;
δ34 = с34 – z34 = 30 – 24 = 6 > 0;
δ42 = с42 – z42 = 36 – (–6) = 42 > 0;
δ43 = с43 – z43 = 121 – 32 = 89 > 0.
Так как все dij > 0, то данный план является оптимальным.
Окончательно представим оптимальный план перевозок (рис. 9, 10).
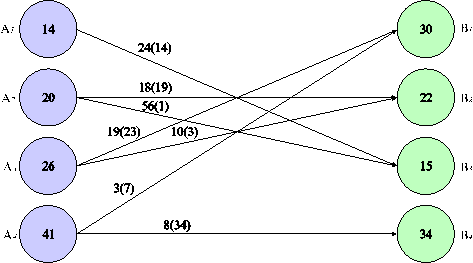
Рис. 9. Оптимальный план перевозок в форме графа
| B | a | |||||
| B1 | B2 | B3 | B4 | |||
| A1 | * | * | * | 14 | ||
| A | A2 | * | * | 20 | ||
| A3 | * | * | 26 | |||
| A4 | * | * | 41 | |||
| b | 30 | 22 | 15 | 34 |
Рис. 10. Оптимальный план перевозок в форме матрицы
Таким образом, в пояснительную записку к расчетному заданию по теме: «Имитационные математические модели» должны входить следующие пункты.
Дата добавления: 2016-02-16; просмотров: 1056;
