Решение транспортной задачи
Суммарные ресурсы в пунктах отправления и назначения равны соответственно a = 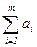 иb =
иb = 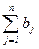 . Если общий объем производства (отправления) груза равен общему объему потребления (назначения), т.е. a = b, то такая задача называется сбалансированной (закрытой). В противном случае имеет место несбалансированная задача (открытая). Кроме того, в общем случае предполагается, что cij
. Если общий объем производства (отправления) груза равен общему объему потребления (назначения), т.е. a = b, то такая задача называется сбалансированной (закрытой). В противном случае имеет место несбалансированная задача (открытая). Кроме того, в общем случае предполагается, что cij 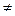 0.
0.
Чтобы вывезти грузы всех поставщиков (условие 1), необходимо, чтобы выполнялось равенство a= 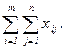 Чтобы удовлетворить заявки всех потребителей (условие 2), необходимо, чтобы выполнялось равенство b=
Чтобы удовлетворить заявки всех потребителей (условие 2), необходимо, чтобы выполнялось равенство b= 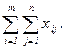
Построение математической модели.Таким образом, задача линейного программирования сводится к транспортной задаче, которая в аналитической форме может быть представлена так:
Функционал Y= 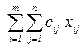 ®min.
®min.
Ограничения
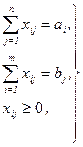
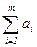 = a,
= a, 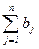 = b, при условии сбалансированности a= b.
= b, при условии сбалансированности a= b.
В случае a 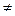 b задача несбалансированна. Для решения такой задачи ее необходимо свести к сбалансированной следующим образом.
b задача несбалансированна. Для решения такой задачи ее необходимо свести к сбалансированной следующим образом.
1. Если a > b, то вводится дополнительный фиктивный склад потребителя bn1=a–b и устанавливается стоимость перевозки ci,n1= 0, (i=1, m);
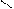 2. Если a < b, то вводится дополнительный фиктивный склад поставщика am1=b–a и устанавливается стоимость перевозки cm1,j = 0, (j=1, n).
2. Если a < b, то вводится дополнительный фиктивный склад поставщика am1=b–a и устанавливается стоимость перевозки cm1,j = 0, (j=1, n).
Целевая функция.Стоимость всех перевозок определяется как сумма произведений стоимости перевозок единицы товара на количество перевозимого по маршруту груза:
Y = c11x11 + c12x12 + … + cijxij + … + cmnxmn, т.е. Y = 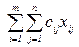 .
.
Если перевозка по данному маршруту не определена, то xij=0.
Критерием оптимизации являются минимальные затраты на доставку всего груза потребителю, т.е. Y® min. Задача сводится к нахождению таких xij, которые удовлетворяют ограничениям задачи и минимизируют суммарные затраты Y. В матричной форме данная задача представлена на рис. 2. В крайнем правом столбце и нижней строке матрицы записаны ресурсы соответствующих поставщиков и потребителей, а в клетках проставляется стоимость перевозки грузов.
| B | a | |||||||
| B1 | B2 | Bj | ... | Bn | ||||
| A1 | c11 | c12 | ... | c1j | ... | c1n | a1 | |
| A2 | c21 | c22 | ... | c2j | ... | c2n | a2 | |
| A | ... | ... | ... | ... | ... | ... | ... | ... |
| Ai | ci1 | ci2 | ... | cij | ... | cin | ai | |
| ... | ... | ... | ... | ... | ... | ... | ... | |
| Am | cm1 | cm2 | ... | cmj | ... | cmn | am | |
| b | b1 | b2 | ... | bj | ... | bn |
Рис. 2. Представление транспортной задачи в матричной форме
Дата добавления: 2016-02-16; просмотров: 533;
