Алгоритм метода аппроксимации Фогеля
1. Вычисление разностей в каждой строке и каждом столбце матрицы между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам ‑ внизу в строке разностей.
2. Поиск максимальной из всех разностей, как по строкам, так и по столбцам (максимальная разность обводится рамкой).
3. Размещение в клетке, где находится наименьшая стоимость перемещения ресурсов для помеченной строки или столбца, максимально возможного количества ресурсов.
Когда все ресурсы отправителя в данной строке будут исчерпаны, строка исключается из дальнейших расчетов (во все клетки данной строки заносится прочерк).
4. Вычисление разностей по столбцам и строкам, без учета стоимости в клетках, имеющих ресурсы, и в клетках исключенных строк или столбцов, и определение максимальной разности в строке и столбце.
5. Поиск минимального элемента в строке или в столбце с максимальной разностью, размещение в данной клетке максимально возможного количества ресурса, после чего возвращение к пункту 4, пока не будут распределены все ресурсы.
Вычисление целевой функции опорного плана
Рассмотрим пример решения транспортной задачи для четырех поставщиков и четырех потребителей товара. Исходные данные транспортной задачи могут быть представлены в форме графа и матрицы (рис. 3 и 4).
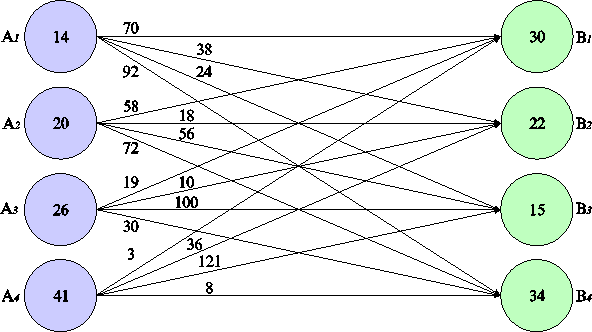 |
Рис. 3. Исходные данные транспортной задачи в форме графа
| B | a | |||||
| B1 | B2 | B3 | B4 | |||
| A1 | 14 | |||||
| A | A2 | 20 | ||||
| A3 | 26 | |||||
| A4 | 41 | |||||
| b | 30 | 22 | 15 | 34 |
Рис. 4. Исходные данные транспортной задачи в форме матрицы
Построим опорный план методом Фогеля (рис. 5).
| B | a | |||||||||||
| B1 (v1) | B2 (v2) | B3 (v3) | B4 (v4) | Столбцы разностей по строкам | ||||||||
| A1 (u1) | * | * | * | 14 | ‑ | ‑ | ‑ | ‑ | ||||
| A | A2 (u2) | * | * | * | 20 | ‑ | ‑ | ‑ | ‑ | ‑ | ||
| A3 (u3) | * | 26 | ||||||||||
| A4 (u4) | * | * | 41 | ‑ | ||||||||
| b | 30 | 22 | 15 | 34 | ||||||||
| ШАГ1 | ||||||||||||
| ШАГ2 | ||||||||||||
| ШАГ3 | ||||||||||||
| ‑ | ШАГ4 | |||||||||||
| ‑ | ‑ | ШАГ5 | ||||||||||
| x | ‑ | x | ‑ | ШАГ6 | ||||||||
| Строки разностей по столбцам |
Рис. 5. Опорный план перевозок
В результате имеем следующий план перевозок:
| Поставщик | Потребитель | Кол-во единиц груза |
| A1 | B3 | |
| A2 | B2 | |
| A3 | B1 | |
| A3 | B2 | |
| A3 | B3 | |
| A4 | B1 | |
| A4 | B4 |
Вычисление целевой функции опорного плана.Суммарные приведенные затраты на перевозку всего груза составляют:
Y0 = c13x13+ c22x22+ c31x31+ c32x32+ c41x41+ c44x44 = 24×14 + 18×20 + 19×23 + 10×2 + 100×1 + 3×7 + 8×34 = 1546 (усл. ед.).
Здесь и далее Yi обозначает, что значение целевой функции относится к i-му шагу оптимизации. Опорный план ‑ Y0.
В настоящее время существует несколько методов последовательного улучшения опорного плана, например распределительный метод, метод потенциалов и т.д. Основой алгоритмов этих методов является критерий оптимальности dij = cij - zij > 0, где cij – затраты, связанные с доставкой одной единицы ресурса из i-го в j-й пункт; zij – расчетные затраты, связанные с доставкой одной единицы ресурса из i-го в j-й пункт, для тех клеток опорного плана, ресурсы в которые не распределены.
Если все δij > 0, то данный план является оптимальным, если нет, то требуется его улучшение.
Дата добавления: 2016-02-16; просмотров: 1365;
