Аналогичная последовательность возникновения полей происходит, если рассмотреть уравнение (9.18) с отличием в том, что существуют электрическоеполе с вектором
EXнапряжённостии магнитноеполе с вектором HZ напряжённости.
Принято (рис.9.3) электрическоеполе плоской электромагнитной волнынаправлять вдоль OZ оси с вектором EZ напряжённости, а магнитноеполе направлять вдоль OX оси с вектором HXнапряжённости, поэтому для математического описания плоской электромагнитной волнывыбрали (9.19) уравнение, положив EX= HZ = 0.
Продифференцируем по y координате первоеуравнение (9.18) и поменяем в смешаннойпроизводной очередностьдифференцирования, вследствие чего получим следующее выражение: ∂2EZ/∂y2 = - μ0μ(∂/∂y)(∂HX/∂t) ↔ ∂2EZ/∂y2 = - μ0μ(∂/∂t)(∂HX/∂y) . (9.20) Подставим в (9.20) из второго(9.18) уравнения выражение∂HX /∂y= - ε0ε(∂EZ /∂t) с учётом (9.9) квадратаc2 = 1/ε0μ0 скорости светав вакууме, вследствие чего получим следующее выражение: ∂2EZ/∂y2 = εμ(∂2EZ/∂t2)/c2. (9.21) Продифференцируем по y координате второеуравнение (9.18) и поменяем в смешаннойпроизводной очередностьдифференцирования, вследствие чего получим следующее выражение: ∂2HX/∂y2 = - ε0ε(∂/∂y)(∂EZ/∂t) ↔ ∂2HX/∂y2 = - ε0ε(∂/∂t)(∂EZ/∂y) .(9.22) Подставим в (9.22) из первогоуравнения (9.18)выражение∂EZ/∂y = - μ0μ(∂HX/∂t) с учётом (9.10) квадратаc2 = 1/ε0μ0 скорости светав вакууме, вследствие чего получим следующее выражение: ∂2HX/∂y 2 = εμ(∂2HX/∂t2)/c2 . (9.23) Сравнивая (9.21), (9.23) с (9. 9), приходим к выводу, что выражения (9.21), (9. 23) являются частнымслучаем трёхмерных волновыхуравнений (9.9) и справедливы для плоской электромагнитной волны, котораяраспространяется в нейтральной, непроводящейсреде с постоянными ε диэлектрической, μмагнитной проницаемостями, в которой равняется нулюρ плотность свободныхзарядов, т.е. ρ= 0, и равняется нулю вектор j = 0 плотноститоков проводимости, т.е. j = 0.
Простейшим решением одномерных волновыхуравнений (9.21), (9. 23) по аналогии с
 sотклонениемот положения равновесия частиц упругой среды в произвольный моментtвремени (рис.2.17) из раздела 2.0 "Колебания и волны" является следующая зависимость проекций EZ, HX на OZ, OX оси координат соответственно векторов напряжённостей EZ электрическогои HX магнитногополя, от tвремении y координатыпо гармоническому(2.69)из раздела 2.0 "Колебания и волны"закону: EZ = Emcos(ωt - ky+ φ1) (9.24) HX = Hmcos(ωt - ky+ φ2) ,
sотклонениемот положения равновесия частиц упругой среды в произвольный моментtвремени (рис.2.17) из раздела 2.0 "Колебания и волны" является следующая зависимость проекций EZ, HX на OZ, OX оси координат соответственно векторов напряжённостей EZ электрическогои HX магнитногополя, от tвремении y координатыпо гармоническому(2.69)из раздела 2.0 "Колебания и волны"закону: EZ = Emcos(ωt - ky+ φ1) (9.24) HX = Hmcos(ωt - ky+ φ2) ,
где ω -циклическая частотаколебаний векторов напряжённостей EZ электрическогополя вдоль OZ оси и HXмагнитногополя вдоль OX оси; k = ω/v (2.70)из раздела 2.0 "Колебания и волны"- волновое число, v = с/(εμ)1/2- фазовая(9.10) скорость плоской электромагнитной волны; Em и Hm - амплитуды колебаний векторов напряжённостейсоответственно EZ электрическогополя вдоль OZ оси и HXмагнитногополя вдоль OX оси; φ1 и φ2 - начальные фазыколебанийвекторовнапряжённостейсоответственно EZ электрическогополя вдоль OZ оси и HXмагнитногополя вдоль OX оси.
 Подставим (9.24) в (9.18) и продифференцируем по tвремении yкоординате, вследствие чего получим следующие выражения: kEmsin(ωt - ky+ φ1) = μ0μωHmsin(ωt - ky+ φ2)
Подставим (9.24) в (9.18) и продифференцируем по tвремении yкоординате, вследствие чего получим следующие выражения: kEmsin(ωt - ky+ φ1) = μ0μωHmsin(ωt - ky+ φ2)
 kHmsin(ωt - ky+ φ1) = ε0εωEmsin(ωt - ky+ φ2) .(9.25) Вследствие равенства функцийв (9.25) равны аргументыи коэффициентыпередэтими функциями, вследствие чего получим следующие выражения: φ1 = φ2; (9.26) kEm = μ0μωHm
kHmsin(ωt - ky+ φ1) = ε0εωEmsin(ωt - ky+ φ2) .(9.25) Вследствие равенства функцийв (9.25) равны аргументыи коэффициентыпередэтими функциями, вследствие чего получим следующие выражения: φ1 = φ2; (9.26) kEm = μ0μωHm
kHm = ε0εωEm . (9.27)
Согласно (9.26) колебания векторов напряжённостей EZ электрическогополя вдоль OZ оси и HXмагнитногополя вдоль OX осипроисходят в одной фазеили синфазно. Разделим в (9.27) первое уравнение на второе, вследствие чего получим следующие выражения: Em/Hm = μ0μHm/ε0εEm ↔ Em/Hm = (μ0μ/ε0ε)1/2. (9.28) Согласно (9.28) отношение Em/Hm амплитуд колебаний векторов напряжённостей EZ электрическогополя вдоль OZ оси и HX магнитногополя вдоль OX оси зависит отпостоянных
ε диэлектрической, μмагнитной проницаемостей среды. Для вакуума, у которого ε = μ = 1,выражение (9.28) принимает следующий вид: Em/Hm = (μ0/ε0)1/2. (9.29)
Плотность энергии плоской электромагнитной волны. Вектор Пойнтинга
Вектор Em напряжённости (рис. 09.0.4)электрическогополя совпадает или направлен противоположно единичному k орту, поэтому в декартовыхкоординатах её вектор Em амплитуды имеет следующий вид: Em =kEZm,(9.30) где EZm - проекция на OZ ось напряжённости электрическогополя в y координате по OY оси и в t время, когда эта напряжённостьотклоняетсяот O координат на максимальное значение, т.е. принимает Em , "- Em" значения.
|
|
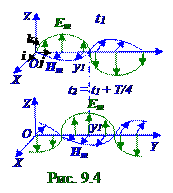
Например (рис.9.4), если в момент t1 временив точке с y1 координатой они имели значение, равное нулю то через интервал времени, равный четвертиT/4 периода колебаний электромагнитной волны, векторы напряжённостей E электрическогополя вдоль OZ осии H магнитногополя вдоль OX оси достигнут максимальногозначения, т.е. (9.30), (9.31)значений Em и Hm .
В произвольный момент t времении произвольной y координатеэлектромагнитная волна, распространяясь по OY оси в направлении единичного j орта,имеет(9.32) векторы E напряжённостейэлектрическогополя вдоль OZ оси и H магнитногополя вдоль OX оси. Вследствие наличия вектора E напряжённостиэлектрическогополя электромагнитная волнав среде с εдиэлектрической проницаемостью обладает (5.152) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" следующей плотностьюwe энергии электрическогополя:
we = ε0εE2/2,(9.33) где E - модуль вектора E напряжённостиэлектрического поля электромагнитной волныв вакууме в произвольный момент t времении произвольной y координате. Вследствие наличия вектора H напряжённостимагнитногополя электромагнитная волнав среде с μмагнитной проницаемостью обладает (8.35) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" следующейплотностьюэнергии магнитногополя: wm = μ0 μH2/2,(9.34)где H - модуль вектора H напряжённостимагнитногополя электромагнитная волнав вакууме в произвольный момент t времении произвольной y координате.
Суммарная w плотность энергии электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями с учётом (9.33) и (9.34) имеет следующий вид: w = we + wm = (ε0εE2/2) + (μ0 μH2/2). (9.35) Преобразуем (9.35) с учётом условия (9.28) Em/Hm = (μ0μ/ε0ε)1/2, справедливого при распространении электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями для значений модулей E, H векторов напряжённостей Eи Hсоответственно электрического и магнитногополей в произвольный момент t времении произвольной y координате, вследствие чего выражение суммарной w плотности энергии электромагнитнойволны имеет следующий вид:
w = (1/2)(ε0εE2ε0εE2)1/2 + (1/2)(μ0 μH2μ0 μH2)1/2 = (1/2)(ε0εE2μ0 μH2)1/2 + + (1/2)(μ0 μH2ε0εE2) 1/2 = (μ0με0ε)1/2EH = (1/v)EH,(9.36) где v = 1/(ε0εμ0μ)1/2 - фазовая скорость электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями по аналогии со скоростью волны в упругой среде(2.75) из раздела 2.0 "Колебания и волны"
Умножим (9.36) на фазовуюv скорость электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями и получим количество S энергии, переносимой электромагнитнойволной через поверхность, перпендикулярную направлению распространения электромагнитнойволны и равной единичнойплощади, за единицу t времени ив данный момент этого t времени. Эта величинаявляется S модулём плотности потокаэнергии и имеет следующий вид: S = vw = EH.(9.37) Векторы E напряжённостейэлектрическогополя вдоль OZ осии H магнитногополя вдоль OX осив произвольной y координате по OY оси и произвольное t время образуют правовинтовуюсистему с направлением распространения волны, совпадающем на рис.9.4 с направлением
j единичного орта.
Направление распространения электромагнитной волны является направлением переноса энергии. Векторное произведение [EH] совпадает (рис.9.4) с направлением j единичного орта, а значит совпадает с направлениемпереноса энергии. В силу взаимной перпендикулярности векторов напряжённостей E электрического и H магнитногополей модуль |[EH]| векторного произведенияс учётом (9.37) равен S модулю плотности потокаэнергии, вследствие чего выражение этого S модуля плотности потокаэнергии электромагнитнойволны имеет следующий вид: |[EH]| = EH = S.(9.38) С учётом (9.38)вектор S плотности потока энергии электромагнитнойволны или векторПойнтингаимеет следующий вид: S = [EH].(9.39) Согласно (9.39) вектор SПойнтингаимеет направление, совпадающее с направлением переноса электромагнитнойволной энергии. Модуль вектораПойнтингаравняетсяS модулю (9.37)плотности потокаэнергии, переносимой электромагнитнойволной.
Теорема Пойнтинга для плоской электромагнитнойволны
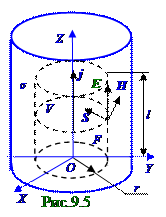
Поток Ф энергии, переносимой электромагнитнойволной через некоторую поверхность с F площадью по аналогии с Фm магнитным (7.17) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" потоком с учётом (9.39) имеет следующий вид: Ф = ∫SdF. (9.40) F По цилиндрическому проводнику (рис. 9.5) с σудельной проводимостьютечёт ток проводимостис постоянным по всему объёму цилиндрического проводника векторомj плотности, направленным перпендикулярнооснованиям этого цилиндра. На участке проводника l длинойсторонниесилы отсутствуют, т.е. нет внешних источниковЭДС, поэтому связь вектора j плотности токовпроводимости в проводникес вектором E напряжённости внешнего электрическогополя описывается (6.19) из раздела 6.0 "Электрический ток" законом Омав дифференциальной форме, вследствие чего выражение вектора j плотности токовпроводимости имеет следующий вид: j = σE, (9.41) где σ - удельная электрическая проводимостьпроводника. Согласно (7.124) из раздела 7.2 "Магнитное поле в веществе" циркуляция вектора H напряжённости магнитного поля поокружности r радиуса и 2πr длиной в области цилиндрического проводника, занятого магнетиком, равна
Iрезрезультирующему макроскопическому или току проводимости через поверхность, которую охватывает эта окружностьr радиусом, вследствие чего выражение циркуляции вектора
H напряжённости магнитного поля поокружности r радиуса имеет следующий вид: H2πr = Iрез . (9.42)
Результирующий Iрез ток проводимости (рис.9.5) через поверхность кругаπr2 площадью с постоянным по всей этой площадиj модулем вектора j плотности токовпроводимости, направленных перпендикулярно кругу, имеет следующий вид: Iрез = jπr2. (9.43)Подставляем (9.43) в (9.42) и получаем следующее выражение, связывающее модуль Hвектора H напряжённости магнитного поля наокружности r радиуса с модулем j вектора j плотности токапроводимости, направленного перпендикулярно кругу πr2 площадью: H2πr = jπr2 ↔ H = jr/2. (9.44)
|
напряжённостей E электрического и H магнитногополей, внутрь(рис.9.5) воображаемого цилиндраVобъёмапо правовинтовойсистеме, т.е. если смотреть из конца вектораSПойнтинга, то для совмещения вектора E с вектором H по кратчайшемупути следует вращать вектор E против"часовой стрелки".
Площадь F боковой поверхности (рис.9.5) воображаемого цилиндра Vобъёмас r радиусом и l длиной имеет следующий вид: F = 2πrl . (9.46) В силу постоянствамодуля (9.45) S вектора SПойнтинга, перпендикулярногок F площадибоковой поверхностивоображаемого цилиндраVобъёмом, втекающийпоток (9.40) Ф энергии, переносимой электромагнитнойволной через эту F площадь боковой поверхности воображаемого цилиндраVобъёма,с учётом (9.45), (9.46) имеет следующий вид:
Ф = ∫SdF= SF = (Ejr/2)2πrl = Ejπr2 l = EjV,(9.47) F
где V = πr2l - объём воображаемого цилиндра(рис. 9.5) с r радиусоми l длиной.Величина Ej в (9.47) с учётом (9.41) закона Омав дифференциальной форме, взятого по модулю, принимает следующий вид: Ej = j2/σ = ρj2, (9.48) где ρ - удельное электрическое сопротивлениепроводника. Величина ρj2 в (9.48) есть количество джоулевой теплоты, поступающей в единичный объём воображаемого цилиндра заединицуtвремени.Умножением ρj2 на весь Vобъёмвоображаемого цилиндра получаем всё количество джоулевой теплоты, поступающей в Vобъём воображаемого цилиндра заединицуtвремени.
Выражение (9.47) есть частный случай теоремы Пойнтингао связиэнергии электромагнитнойволны сджоулевой теплотой, выделяющейся в проводнике в случае отсутствия стороннихсил, т.е. когда внешние источникиЭДС отсутствуют. Векторы E напряжённости электрическогои H магнитногополей на F площади (рис.9.5) боковойповерхности воображаемого цилиндра
Vобъёмаможно рассматривать присущими электромагнитной волне, которая переносит энергиюпо направлению вектора S Пойнтинга.
Энергия и импульс плоской электромагнитной волны
Поглощаясь в каком-либо M теле (рис.9.6), электромагнитная волнасообщает этому телу некоторый импульс, т.е. оказывает на него давление. Плоская электромагнитная волна, т.е. такая, у которой векторы E напряжённостейэлектрическогои H магнитногополей, находящиеся в равных фазах, лежат в плоскости, например, (рис.9.6) M тела, имеет вектор S Пойнтинга, перпендикулярный плоскости этого M тела. Плоское M тело имеет малую величину удельной
σэлектрической проводимостии постоянные ε диэлектрическую и μмагнитную проницаемости, равные единице. На (рис.9.6) плоскости M тела сторонниесилы отсутствуют, т.е. нет внешних источниковЭДС, поэтому связь вектора j плотности токапроводимости в M теле с вектором E напряжённости внешнего электрическогополя описывается (6.19) из раздела 6.0 "Электрический ток" законом Омав дифференциальной форме, вследствие чего выражение вектора j плотности токапроводимости имеет следующий вид: j = σE, (9.49)
|
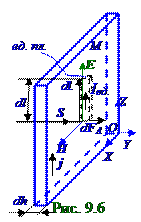
проницаемости,имеет следующий вид: dFA= j[dl, B] = μ0[jdl, H], (9.50) где dl = dlj/j - вектор(7.73) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях", имеющий направление вектора j плотности тока проводимости имодуль, равный (рис.9.6) малойdl длине проводника. Подставляем в (9.50)векторdl = dlj/j и получаем следующее выражение для элементарного вектора dFA силы Ампера, действующего на проводниксвектором j плотности токапроводимости малойdl длины, который помещён в магнитное поле с вектором H напряжённостимагнитного поля: dFA= μ0dl[j, H]. (9.51)
Для вектора FA ед.об. силы Ампера, действующего не на проводникмалойdl длиной, а на проводник единичнойдлины и имеющего единичную площадь поперечного сечения, т.е. на проводник единичного V0 объёма, мысленно вырезанного из M тела, выражение (9.51) преобразуется к следующему виду: FA ед.об.= μ0[j, H]. (9.52)
Дата добавления: 2016-02-14; просмотров: 1702;
