Электромагнитное поле. Инвариатность заряда и теоремы Гаусса в выбранной инерциальной системе отсчёта
Электрическиезаряды, неподвижные относительно выбранной инерциальной системыотсчёта (ИСО), образуют в окружающем эти заряды пространстве электростатическое поле, характеризующихся вектором Eнапряжённости этого электростатического поля. Магнитное поле в окружающем неподвижныеэлектрические заряды пространстве отсутствует.
Если электрический заряд в выбранной ИСО движется, то в этой ИСО существует в рассматриваемой точке пространстве кроме электрическогополяс (5.6) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" результирующимвектором E напряженности также и магнитное поле (7.7) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" с векторомB магнитной индукции. При этом в каждой точке пространства выбранной ИСО с движущимися зарядами модули E, B векторов E напряженностиэлектрическогополя и B индукции магнитного поля переменны во tвремени.
Поэтому электрическоеполе с вектором E напряженности и магнитное поле с вектором
B магнитной индукции являются различными компонентами единой материи, которое называется электромагнитным полем.
Заряд q любой частицы не зависитот величины и направления её вектора скорости в выбранной ИСО, т.е. q заряд любой частицы является инвариантной величиной по отношению к выбору ИСО, в которой этот q заряд измеряется.
ТеоремаГаусса (5.17) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" для электрическогополя в интегральной форме в вакууме для одиночного qi заряда, имеющая следующий вид: NE = ∫EdS = qi/ε0,
(S)
применима не только для покоящегося одиночного qi заряда, но и движущегося в выбранной ИСО
qi заряда, т.е.эта теоремаГаусса справедлива во всех ИСО. При этом поверхностный интеграл в теоремеГаусса (5.17) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля" для электрическогополяв случае движущегося в выбранной ИСО одиночного qi заряда следует вычислять полностью в заданный момент tвремени.
Преобразования Лоренца векторов Eнапряжённости электрического и Bиндукции магнитного полей в различных инерциальных системах отсчёта
Векторы E′ напряженности электрического и B′ индукции магнитного полей в K′(x′,y′,z′,t′) подвижнойИСОпри (рис. 9.1) её движении вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО с векторомvпостоянной скорости связаны с векторами E напряженности электрического и B индукции магнитного полей впроизвольнойM точке пространства неподвижнойИСО с использованием(3.11) из раздела 3.0 "Релятивистская механика" частных преобразованийЛоренца следующими соотношениями:
E||′ = E||; B||′ = B||; E┴′ =(E┴ + [v,B])/[1-(v2/c2)]1/2; B┴′ =[B┴ -([v,E])/c2]/[1-(v2/c2)]1/2, (9.1)
|
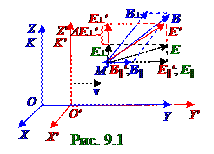
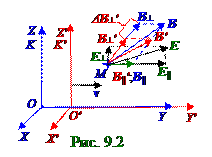
E┴′,E┴ -составляющие (рис. 9.1) векторов E′, E напряжённости электрическогополя, перпендикулярные вектору vпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО; B||′ = B|| - равные(рис. 9.2) составляющие векторов B′, B индукции магнитного поля, параллельные векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО; B┴′,B┴ -составляющие (рис. 9.2) векторов B′, B индукции магнитного поля, перпендикулярные векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО.
Составляющие(рис. 9.1) E┴′,(рис. 9.2) B┴′векторов E′, B′ в K′(x′,y′,z′,t′) подвижнойИСОсоответственно напряжённости электрическогополя и индукции магнитного поля, перпендикулярные векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО, отличаются согласно (9.1) от составляющих(рис. 9.1) E┴,(рис.9.2) B┴ векторов E, Bв K(x,y,z,t) неподвижнойИСО соответственно напряжённости электрическогополя, индукции магнитного поля на ΔE, ΔB величины. Например, при отсутствии в K(x,y,z,t) неподвижнойИСО составляющей(рис.9.1) E┴ вектора напряжённости электрическогополя, перпендикулярного векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО, но наличияв K(x,y,z,t) неподвижнойИСО составляющей
B┴ вектора индукции магнитного поля в K′(x′,y′,z′,t′) подвижнойИСОвозникаетсоставляющаявектора напряжённости электрическогополя,равная ΔE┴′ величине и направленная (9.1) по O′Z′ оси.
Например, при отсутствии в K(x,y,z,t) неподвижнойИСО составляющей(рис.9.2) B┴ вектора индукции магнитного поля, перпендикулярного векторуvпостоянной скорости, с которой K′(x′,y′,z′,t′) подвижнаяИСОдвигается вдоль положительного направления OY осиK(x,y,z,t) неподвижнойИСО, но наличияв K(x,y,z,t) неподвижнойИСО составляющей E┴ вектора напряжённости электрическогополя в K′(x′,y′,z′,t′) подвижнойИСОвозникаетсоставляющаявектора индукции магнитного поля,равная ΔB┴′ величине и направленная (9.1) противоположно O′X′ оси.
Волновое уравнение для электромагнитного поля. Скорость распространения электромагнитных волн
Для случая однородной, незаряжённой, т.е. с плотностью свободныхзарядов ρ = 0, непроводящей, т.е. с вектором j = 0плотноститоков проводимости,среды,что выполняется, например, для вакуума, первые производныепо tвремениот левойи правойчастей выражения (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля", связывающихвектор D электрического смещенияс вектором E напряжённости электрическогополя, и первые производныепо tвремениот левойи правойчастей выражения(7.127) из раздела 7.2 "Магнитное поле в веществе", связывающих вектор B магнитной индукции с напряжённостью H магнитного поля, имеют следующий вид: ∂D/∂t= ε0ε∂E/∂t;
∂B/∂t= μ0μ∂H/∂t. (9.2)
Подставим (9.2) в дифференциальную форму уравнений Максвелла(8.69), (8.77) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля", вследствие чего эти выражения (9.2) принимают следующий вид: [ E] = - ∂B/∂t ↔ [ E] = - μ0μ∂H/∂t; [H] = (∂D/∂t) ↔ [H] = ε0ε∂E/∂t,(9.3) где в уравнении полного тока в теории Максвелла(8.77) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" [H] = j + (∂D/∂t) вектор плотноститоков проводимости среды, вследствие отсутствия её проводимости, равен нулю, т.е. j = 0.
Возьмём роторот обеих частей в 2-ух уравнениях (9.3), вследствие чего имеют место следующие выражения: [ [ E]] = - μ0μ[∂H/∂t] ;
[[H]] = ε0ε[∂E/∂t]. (9.4) Т.к. согласно (7.117) из раздела 7.2 "Магнитное поле в веществе" операция определения роторасвязана с вычислением производныхпоосямдекартовых координат, то в (9.4) можно произвести дифференцирование по t времени после определения ротора, т.е. вынести ∂/∂t оператор в правойчасти 2-ух уравнений (9.4) перед ротором, вследствие чего эти выражения (9.4) принимают следующий вид: [ [ E]] = - μ0μ(∂/∂t)[H] ;
[[H]] = ε0ε(∂/∂t)[E] .(9.5)В левой части (9.5) возьмём двойное векторное произведение, а в правую часть подставим (9.3) с учётом двойного дифференцированияпо tвремени, вследствие чего выражения (9.5) принимают следующий вид:(E) - E( ) = - μ0με0ε ∂2E /∂t2↔ (E) - ∆E = - μ0με0 ε∂2E /∂t2;
( H) - H ( ) = - ε0εμ0μ∂2H/∂t2 ↔ ( H ) - ∆ H = - μ0με0ε∂2H/∂t, (9.6)
где= i(∂/∂x) + j(∂/∂y) + k(∂/∂z) - векторный дифференциальный операторили операторнабла; ( ) = (∂2/∂x2 )+(∂2/∂y2 ) + (∂2/∂z2 ) = ∆ - скалярноепроизведение двух операторовнабла есть ∆ -оператор Лапласа.
Учтём в дифференциальной форме уравнения Максвелла (5.21)из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"равенство нулюплотности свободныхзарядов,
т.е. ρ = 0, а в дифференциальной форме уравнения Максвелла (7.20) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" равенство нулюdivBвектораB магнитной индукции, вследствие чего получим следующие выражения: E = 0;
H = 0.(9.7) Подставим (9.7) в (9.6) с учётом 0 = 0 и получим следующие выражения: ∆E = μ0με0ε∂2E/∂t2;
∆H = ε0εμ0μ∂2H/∂t2. (9.8) Введём в (9.8) полную (9.6) форму оператора ∆Лапласаи получим следующиедва волновыхуравнения: (∂2E/∂x2)+(∂2E/∂y2) + (∂2E/∂z2) = (εμ/c2)(∂2E/∂t2); (∂2H/∂x2)+(∂2H/∂y2) + (∂2H/∂z2) = (εμ/c2)(∂2H/∂t2), (9.9) где c2 = 1/ε0μ0 - квадратскорости электромагнитной волныв вакууме.
Всякая функция, удовлетворяющая (9.9), описывает некоторую волну, причём корень квадратныйиз величины, обратной коэффициентупри производнойпо tвременив правой части (9.9), даёт фазовуюскорость этой волны. Следовательно, уравнение (9.9) указывает на то, что электромагнитные полямогут существовать в виде электромагнитных волн, фазовая vскорость которых имеет следующий вид: v = с/(εμ)1/2 . (9.10) В вакууме при равенстве единицепостоянных диэлектрической и магнитнойпроницаемостей соответственно ε = μ = 1 с учётом (10.9) скорость vэлектромагнитных волнравна скорости с света.
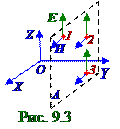
Волновое уравнения плоской электромагнитной волны, его решение
Плоская(рис.9.3)электромагнитная волна,подобная упругой плоской волне (рис.2.17) из раздела 2.0 "Колебания и волны", распространяется в нейтральной, непроводящейсреде с постоянными ε диэлектрической и μмагнитной проницаемостями, равенства нулюρ плотности свободныхзарядов, т.е. ρ= 0, и равенства нулю вектора j = 0 плотноститоков проводимости, т.е. j = 0. Ось OY (рис.9.3) перпендикулярнаA плоскости равных фаз, т.е. характеристики электромагнитной волныв т.т.1, 2 и 3 одинаковы, поэтому векторы E, H напряжённостив этих т.т. 1, 2 и 3 соответственно
|
(∂EZ/∂y) - (∂EY/∂z) = - ∂BX/∂t; (∂EX/∂z) - (∂EZ/∂x) = - ∂BY/∂t; (∂EY/∂x) -(∂EX/∂y) = - ∂BZ/∂t
с учётом ∂EY/∂x = 0; ∂EY/∂z = 0; ∂EZ/∂x = 0; ∂EX/∂z = 0 в пределах (рис. 09.0.3) плоскости A равных фазимеет следующий вид: ∂EZ/∂y = - ∂BX/∂t ↔ ∂EZ/∂y = - μ0μ(∂HX/∂t); 0 = ∂BY/∂t ↔ 0 = μ0μ(∂HY/∂t);
∂EX/∂y = ∂BZ/∂t ↔ ∂EX/∂y = μ0μ(∂HZ/∂t),(9.11) где BX= μ0 μHX, BZ = μ0 μHZ-проекциинаOX, OZ оси вектора B магнитной индукции, связанные с HX, HZ проекцияминаэтижеоси вектора H напряжённостимагнитного поля согласно (7.127) из раздела 7.2 "Магнитное поле в веществе";
б) из (7.20) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" , (табл. 8.1) из раздела 8.0 "Переменные электрические и магнитные поля. УравненияМаксвелла" (∂BX/∂x) + (∂BY/∂y)+ (∂BZ/∂z) = 0 с учётом ∂BX/∂x= 0; ∂BZ/∂z = 0 в пределах (рис. 09.0.3) плоскости A равных фазимеет следующий вид:
∂BY/∂y = 0 ↔ μ0μ(∂HY/∂y) = 0, (9.12) где BY= μ0 μHY -проекциянаOY ось вектора B магнитной индукции, связанная с HY проекцией наэтужеось вектора H напряжённостимагнитного поля согласно (7.127) из раздела 7.2 "Магнитное поле в веществе";
в) из (8.78), (табл. 8.1) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" (∂HZ /∂y) - (∂HY /∂z) = jx + (∂DX /∂t); (∂HX/∂z) - (∂HZ /∂x) = jy + (∂DY/∂t); (∂HY /∂x) - (∂HX /∂y) = jz + (∂DZ /∂t) с учётом ∂HY /∂x= 0; ∂HY /∂z = 0; ∂HZ /∂x = 0; ∂HX/∂z = 0, а также с учётом равенства нулю вектора j = 0 плотноститоков проводимости, т.е. j = 0, вследствие чего jx = 0; jy= 0; jz = 0, в пределах (рис. 09.0.3) плоскости A равных фазимеет следующий вид: ∂HZ /∂y = ∂DX /∂t ↔ ∂HZ /∂y = ε0ε(∂EX /∂t); 0 = ∂DY/∂t ↔ 0 = ε0ε(∂EY /∂t);
∂HX /∂y = - ∂DZ /∂t ↔ ∂HX /∂y = - ε0ε(∂EZ/∂t).(9.13) г) из (5.88) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля", (табл. 8.1) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля" (∂DX/∂x) + (∂DY/∂y)+ (∂DZ/∂z) = ρ с учётом ∂DX/∂x = 0; ∂DZ/∂z = 0, а также с учётом равенства нулюρ плотности свободныхзарядов, т.е. ρ= 0, в пределах (рис.9.3) плоскости A равных фазимеет следующий вид: ∂DY/∂y = 0 ↔ ε0ε(∂EY /∂y) = 0.(9.14) где DY= ε0εEY -проекциянаOY ось вектора D электрического смещения, связанная с EY проекцией наэтужеось вектора E напряжённости электрическогополя согласно (5.87) из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля"
Согласно (9.11), (9.12) справедливы следующие выражения: ∂HY/∂t = ∂HY/∂y = 0.(9.15)Согласно (9.13), (9. 14) справедливы следующие выражения: ∂EY/∂t = ∂EY/∂y = 0.(9.16) Равенство нулю первых производныхв (10.14), (10.15) по t времении y координатеот проекций EY, HY векторов E, H напряжённостисоответственно электрического и магнитногополей на OY ось координат при изменяющемсяво tвремени электромагнитномполе в произвольной
y координатепространства возможно, если эти проекции EY, HY векторов E, H напряжённостисоответственно электрического и магнитногополей на OY ось координат имеют следующий вид: EY = HY = 0.(9.17) С учётом (9.17) уравнения (9.12) и (9.14) исключаются. Из уравнений (9.11) и (9.13) сгруппируем следующие две системы издвух уравнений, в которые входят проекции EX, HZ и EZ, HX на OY, OZ оси векторов E, H напряжённостисоответственно электрического и магнитногополей: ∂EZ/∂y = - μ0μ(∂HX/∂t) (9.18)
∂HX /∂y= - ε0ε(∂EZ /∂t) ;
∂EX/∂y = μ0μ(∂HZ/∂t)
∂HZ/∂y = ε0ε(∂EX /∂t) . (9.19)
В уравнения (9.18), (9.19) входят только проекцииEZ, HX и EX, HZот векторов E, H напряжённостисоответственно электрического и магнитногополей по OX, OZ осям координат, т.к.согласно (9.17)проекцииEY, HY, т.е. направленные по OY оси координат,равны нулю. Для описания плоской электромагнитной волныдостаточно взять одно из уравнений (9.18) или (9.19). Допустим, что первоначальнобыло созданопеременноево tвремениэлектрическоеполе с вектором
EZ напряжённости, направленное (рис.9.3) вдоль OZ оси. Согласно второму(9.18) уравнению переменноево t времениэлектрическоеполес вектором EZ напряжённостиэлектрическогополя, создаст магнитноеполе с вектором HXнапряжённости, направленное вдоль OX оси. Электрическоеполе с вектором EX напряжённости, направленное вдоль OX оси и магнитноеполе с вектором HZ напряжённости, направленное вдоль OZ оси, при этом не возникают.
Дата добавления: 2016-02-14; просмотров: 859;