Модуль FA ед.об. (9.52) вектора FA ед.об. силы Ампера, действующего на проводник единичного
V0 объёма, определяется с учётом перпендикулярности векторов j плотности тока проводимости и H напряжённостимагнитного поляэлектромагнитной волны, т.к.вектор j плотноститока проводимости коллинеарен вектору E напряжённостиэлектрическогополяэлектромагнитной волны, а вектора H напряжённостеймагнитного и E электрическогополей в электромагнитной волне взаимно перпендикулярны, вследствие чего этот модульFA ед.об. вектора FA ед.об.силы Ампера имеет следующий вид: Fед.об. = μ0 jH. (9.53) Поверхностному слою (рис.9.6) тела M с единичным V0 объёмом и dh толщиной вектором Fед.об. (9.52) силы Ампера сообщается в единицуtвременимодульdKвектораdK импульсаcилы (1.43) из раздела 1.0 "Физические основы механики", который с учётом (9.53) имеет следующий вид: dK = Fед.об.dh = μ0 jHdh. (9.54) В этом же слое dh толщиной в единицуt временисогласно (9.48) поглощаетсяdW энергия, которая имеет следующий вид: dW = Ejdh, (9.55)
где (9.48) Ej - количество джоулевой теплоты, поглощаемой единичнымV0 объёмом. Возьмём отношение (9.54), (9.55) и получим следующее выражение для отношения K модуля вектораKимпульсаcилы, действующего на проводник произвольного Vобъёма в единицуt времени, к количеству Wджоулевой теплоты, поглощаемойэтим проводником произвольного Vобъёма в единицуt времени: dK/dW = μ0H/E ↔ K/W = μ0H/E. (9.56) Подставим в(9.56) соотношение ε01/2E = μ01/2H (9.29), справедливое при распространении плоской электромагнитнойволны в вакууме для значений модулей E, H векторов
Eи H напряжённостейсоответственно электрического и магнитногополей в произвольный момент t времении произвольной y координате, вследствие чего это выражение(9.56) принимает следующий вид: K/W = (ε0μ0)1/2 = 1/c, (9.57) где с = 1/(ε0 μ0)1/2 - скоростьсвета в вакууме. Согласно (9.57) плоская электромагнитнаяволна, несущая в единицуt времени
W энергию, обладает модулем KвектораKимпульсаcилы, действующего на проводник произвольного Vобъёма в единицуt времени, который определяется следующим выражением: K = W/c. (9.58) Если проводник имеет единичный V0 объём, то в выражении (9.58) нужно использовать суммарную (9.35) w плотность энергии электромагнитнойволны и модуль Kед.об.вектора
K ед.об.импульсаcилы, действующего на проводник единичного V0 объёма в единицуt времени, в связи с чем выражение (9.58) принимает следующий вид: Kед.об.= w/c. (9.59)Согласно(9.37) связь суммарной w плотности энергии плоской электромагнитнойволны, распространяющейся в вакууме, с модулём Sплотности потокаэнергии, т.е. с модулем вектора SПойнтинга, имеет следующий вид: w = S/c. (9.60) Подставляем (9.60) в (9.59) и получаем следующее выражение, использующее модульS вектора SПойнтинга, для модуляKед.об.вектора Kед.об.импульса, передаваемого плоской электромагнитнойволной проводнику единичного V0 объёма в единицуt времени: Kед.об.= S/c2. (9.61) Выражение для вектора Kед.об импульссучётом сонаправленности этого Kед.обвектораимпульса, передаваемого плоской электромагнитнойволной в вакууме проводнику V0 объёма единичного объёма в tединицу времени, вектору SПойнтинга,а такжес учётом связи (9.39) вектора SПойнтингаи векторов E напряжённостейэлектрическогои H магнитногополейэлектромагнитной волныимеет следующий вид: Kед.об. = S/c2 = [E,H]/c2 ↔ S = c2 Kед.об. (9.62) Согласно (9.62) при переносев вакууме энергииплоскойэлектромагнитнойволной вектор S плотности потока энергии равен вектору Kед.об импульса, передаваемого этой электромагнитнойволной проводнику единичного V0 объёма в единицуt времени, умноженному на квадрат c2 скорости света в вакууме.
Волновой характер электромагнитного поля движущегося заряда
Заряд Q имеет ρ(x, у, z, t) плотность заряда (рис.9.7), зависящую от t времении
x, у и z координат, в шаре V объёмом с R радиусом, который намного меньше
r расстояния до M точки, в которой определяется поле электромагнитнойволны, т.е. R << r.
Заряд Q c ρ(x, у, z, t) плотностью этого заряда двигается по OZ оси как единое целое с вектором u скорости, модульu которого много меньше v = 1/(ε0εμ0μ)1/2 фазовой скорости электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями, т.е. u << v.
|
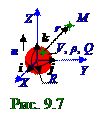
данный момент t времени по OZ оси.
Согласно закону Био - Савара - Лапласа и принципу суперпозиции(7.6) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" результирующий вектор BM магнитнойиндукции в данной M точке от движущегося Q зарядаc ρ(x, у, z, t) плотностью в среде с постоянными ε диэлектрической и
μмагнитной проницаемостями, равняется следующему интегралу:
BM = (μμ0/4π)∫([ jт, r]/r3) dV, (9.64)
V
где r - радиус-вектор, проведённый из точкис координатами x, у, z, находящейся внутри шара V объёмом с R радиусом и Q зарядом, в M точку с координатами xM, уM, zM, в которой в данный момент t времени определяется магнитная индукция; r = [(xM - x)2 + (yM - y)2 +(zM -z)2]1/2- модуль r радиуса-вектораили расстояние между точкойс координатами x, у, z, находящейся внутри шара V объёмом с R радиусом и Q зарядом, и M точкой с xM, уM, zM координатами, в которой в данный момент t времени определяется магнитная индукция.
Векторное [jт,r] произведение (9.64) в прямоугольной декартовой системекоординат с учётом равенства нулю в произвольный момент t времени проекций jтX, jтY по OX, OZ осямвектора
jт(x, у, z, t)плотности тока проводимости, т.е. jтX = 0, jтY = 0,имеет следующий вид:
[jт, r]= -jтZ (yM - y)i + jтZ (xM - x)j . (9.65)
Подставим (9.65) в (9.64) и получим следующее выражение результирующего вектора
BM магнитнойиндукции в (рис.9.7) данной M точке от движущегося Q зарядаc
ρ(x, у, z, t) плотностью в среде с постоянными относительными ε диэлектрической и μмагнитной проницаемостями: BM = (μμ0/4π)∫{[- jтZ (yM - y)i + jтZ (xM - x)j]/r3} dV, (9.66) V
где r = [(xM - x)2 + (yM - y)2 +(zM -z)2]1/2- модуль r радиуса-вектораили расстояние между точкойс координатами x, у, z, находящейся внутри шара V объёмом с R радиусом и Q зарядом, и M точкой с координатами xM, уM, zM, в которой в данный момент t времени определяется магнитная индукция.
Представим результирующий вектор BM магнитнойиндукции в (рис.9.7) данной M точке от движущегося Q зарядаc ρ(x, у, z, t) плотностью в среде с постоянными ε диэлектрической и μмагнитной проницаемостями в следующем виде: BM = (μμ0/4π)rot∫(jт/r)dV, (9.67) V
Cогласно правилам вычисления ротации ротор от суммы векторов равен сумме роторов от каждого из векторов, входящих в эту сумму, поэтому (9.67) принимает следующий вид:
BM = (μμ0/4π)rot∫(jт/r)dV = (μμ0/4π)∫rot(jт/r)dV, (9.68) V V
Cогласно (5.42) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" координаты (9.68) ротации в прямоугольной декартовой системекоординат с учётом равенства нулю в произвольный момент
t времени производных ∂jтX/∂x, ∂jтX/∂y, ∂jтX/∂z и ∂jтY/∂x, ∂jтY/∂y , ∂jтY/∂z от соответствующих проекций jтX, jтY по OX, OY осямвектора jт(x, у, z, t)плотности тока проводимости, т.е. ∂jтX/∂x= 0, ∂jтX/∂y = 0,∂jтX/∂z = 0 и ∂jтY/∂x = 0, ∂jтY/∂y = 0, ∂jтY/∂z = 0, имеют следующий вид:
rot(jт/r)= i ∂{jтZ/[(xM - x)2 + (yM - y)2 +(zM -z)2]1/2}/∂y - j∂{ jтZ/[(xM - x)2 + (yM - y)2 +(zM -z)2]1/2}/∂x ↔
↔ rot(jт /r)= - ijтZ(yM - y)/[(xM - x)2 + (yM - y)2 +(zM - z)2]3/2} + j{ jтZ(xM - x)/[(xM - x)2 + + (yM - y)2 +(zM -z)2]3/2} ↔ rot(jт /r)= [-jтZ (yM - y)i + jтZ(xM - x)j]/r3, (9.69)
где учтено, что амплитуда jтZплотности тока проводимостипо OZ оси величина постоянная, т.е. jтZ = const, а также использовано правило дифференцирования отношения функций и
"цепного правила" при дифференцировании.
Подставим (9.69) в (9.68) и получим следующее выражение результирующего вектора
BM магнитнойиндукции в (рис.9.7) данной M точке от движущегося Q зарядаc ρ(x, у, z, t) плотностью в среде с постоянными ε диэлектрической и μмагнитной проницаемостями, равного выражению (9.66): BM = (μμ0/4π)∫{[ - jтZ (yM - y)i + jтZ (xM - x)j]/r3} dV, (9.70) V
Вследствие равенства (9.70), которое получено преобразованием (9.67), выражению (9.66), которое получено преобразованием (9.64), возможно приравнять (9.64) и (9.67), вследствие чего результирующий вектор BM магнитнойиндукции в (рис.9.7) данной M точке от движущегося Q зарядаc ρ(x, у, z, t) плотностью в среде с постоянными ε диэлектрической и μмагнитной проницаемостями можно представить в следующем виде: BM = (μμ0/4π)∫([jт,r]/r3) dV= (μμ0/4π)rot∫(jт/r)dV, (9.71) V V
Вектор B индукциимагнитногополя, создаваемый током проводимости с вектором jт(x, у, z, t)плотности, в (рис. 9.7) произвольной M точке пространства в среде с постоянными относительными ε диэлектрической и μмагнитной проницаемостями, имеет на основании (9.71) следующий вид: BM ≈ (μμ0/4π)rot{(1/r)∫uρ[t - (r/v)]dV ,(9.72) V
где [t - (r/v)] - параметр по аналогии (2.69) из раздела 2.0 "Колебания и волны", учитывающий ρ плотность заряда в шаре V объёмом с R радиусом, а также учитывающий τ = r/vвременное запаздывание, согласно которому вектор B индукциимагнитногополяв M точке, находящейся на r расстоянии от заряженного шара V объёмом будет определяться не ρ(t) плотностью заряда в этом шаре V объёмом в данный момент t времени, а ρ[t - (r/v)] плотностью заряда в заряженном шаре
V объёмом, которое было раньше данного момента t временина величину τ = r/vвременного запаздывания, за которое электромагнитнаяволна с v = 1/(ε0εμ0μ)1/2 фазовой скоростьюраспространится от заряженного шара V объёмом до M точки; 1/r - обратнаявеличина r расстояния от заряженного шара V объёмом до M точки, в которой определяется вектор B индукциимагнитногополя,вынесен за знак интеграла, поскольку это r расстояние намного больше R радиуса заряженного шара, т.е. r >>R, а интегрирование ведётся по V объёму, поэтому для удалённой на r расстояние M точки заряженный шар можно считать (рис.5.2), (рис.5.3) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" точечным Q зарядом; jт(x, у, z, t) = uρ[t - (r/v)] - вектор плотности тока проводимости, вызванный (9.72) движением Q заряда по OZ оси как единое целое с вектором u скорости, который был раньше данного момента t временина величину τ = r/vвременного запаздывания, за которое электромагнитнаяволна с v = 1/(ε0εμ0μ)1/2 фазовой скоростьюраспространится от заряженного шара V объёмом до M точки.
Поскольку Q заряд ρ плотностью (рис. 9.7) двигается как единое целое, т.е. все части этого
Q заряда двигаются с одинаковойскоростью, в выражении (9.72) из под знака интеграла может быть вынесен вектор u скорости движения этого заряда, вследствие чего это выражение примет следующий вид: BM ≈ (μμ0/4π)rot(u/r)∫ρ[t - (r/v)]dV = {μμ0Q[t - (r/v)]/4π}rot(u/r),(9.73) V
где Q[t - (r/v)] = ∫ρ[t - (r/v)]dV - полный заряд ρ плотностью в заряженном шаре V объёмом, который был
V
раньше данного момента t временина величину τ = r/vвременного запаздывания, за которое электромагнитнаяволна с v = 1/(ε0εμ0μ)1/2 фазовой скоростьюраспространится от заряженного шара V объёмом до M точки, в которой определяется вектор BM индукциимагнитногополя.
Вектор (рис.9.7) pQдипольногоэлектрического момента (5.61) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" полного Q заряда, имеющего z координату, имеет следующий вид: pQ= Qzk, (9.74)
где k - единичный (1.1) из раздела 1.0 "Физические основы механики" векторпоOZоси.
Первая pQ′ производная по tвремениот вектора (9.74) pQдипольногоэлектрического момента имеет следующий вид: pQ′ = Q(dz/dt)k = uQ ↔ u = pQ′/Q , (9.75)
где u = j(dz/dt)- вектор u скорости Q зарядаc ρ(x, у, z, t) плотностью, направленный в данный момент t времени по OZ оси.
Подставляем (9.75) в (9.73) и получаем выражение вектора BM индукциимагнитногополя в произвольной M точке пространства, находящейся (рис.9.7) на r расстоянии от заряженного шара V объёмом, считая его точечным Q зарядом, в среде с постоянными ε диэлектрической и μмагнитной проницаемостямив зависимости от величины первой pQ′ производной по tвремениот вектора (10.74) pQдипольногоэлектрического момента, которое имеет следующий вид: BM ≈ (μμ0/4π)rot {pQ′[t - (r/v)]/r},(9.76)
где pQ′[t - (r/v)]-первая производная по tвремениот вектора (9.74) pQдипольногоэлектрического момента, учитывающая величину Q[t - (r/v)] заряда шара V объёмом, который был раньше данного момента t временина величину τ = r/vвременного запаздывания, за которое электромагнитнаяволна с v = 1/(ε0εμ0μ)1/2 фазовой скоростьюраспространится от этого заряженного шара V объёмом до M точки, в которой определяется вектор B индукциимагнитногополя.
Определение электромагнитного поля движущегося точечного заряда
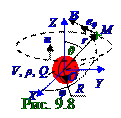
Заряд Q c ρ плотностью этого заряда двигается (рис.9.8) по OZ оси с вектором u скорости, т.е. вектор jт плотности тока направлен по OZ оси, поэтому (рис.7.3) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" векторB индукции магнитного поля от этого движущегося Q заряда находится на окружности, плоскость которой параллельна координатной OXY плоскости. С использованием (5.42) из раздела 5.1 «Электростатика» определяем следующие проекцииBMX , BMY соответственно на OX, OY оси (9.76) вектора BM индукциимагнитногополя (рис.9.8) впроизвольной M точке пространства
|
BMY = (μμ0/4π)(x/r2){(1/r) pZQ′[t - (r/v)] + (1/v)pZQ′′[t - (r/v)]} ≈ (μμ0/4π)(x/r2){1/v)pZQ′′[t - (r/v)]}, (9.78)
где pZQ′′[t - (r/v)] - вторая производная по tвремениот вектора (10.74) pQдипольногоэлектрического момента Q заряда; r = (x2 + у2 + z2)1/2 - модуль (рис. 09.0.8) r радиуса-вектораили расстояние между шаром V объёмом с R радиусом и Q зарядом, и M точкой с координатами x, у, z, в которой в данный момент t времени определяется магнитная индукция; r >>R - расстояние от заряженного шара V объёмом до M точки, в которой определяется вектор BM индукциимагнитногополя, поэтому для удалённой на r расстояние M точки заряженный шар можно считать (рис.5.2), (рис.5.3) из раздела 5.1 "Электростатика"точечным Q зарядом; знак " ≈" использован потому, что для случая большого r расстояния произвольной M точки пространства, в которой определяется вектор
BM индукции магнитного поля, от Q заряда, т.е. при r → ∞, первым (1/r)pZQ′[t - (r/v)] слагаемым в (9.77), (9.78) можно пренебречь по сравнению со вторым (1/v)pZQ′′[t - (r/v)] слагаемым.
ПроекцияBZ на OZ осьвектора BM индукциимагнитногополя (рис.9.8) впроизвольной M точке пространства равна нулю, т.к. векторBM индукции магнитного поля от движущегося по OZ оси Q заряда находится на окружности, плоскость которой параллельна координатной OXY плоскости.
В сферической системе координат вектор BM индукциимагнитногополя согласно выражению сферических координат через декартовы имеет проекцию BMφ, отличную от нуля, по направлению
(рис.9.8) eφ орта, вследствие чего выражение вектора BM индукциимагнитногополя в M точке имеет следующий вид: BM = (μμ0/4πr){(1/v) pZQ′′[t - (r/v)]}sinθeφ, (9.79)
где θ - угол, называемый в сферической системе координат полярным расстоянием.
ВекторHM напряжённости магнитного поляв произвольной M точке пространства, возникающего вследствие движения Q заряда (рис.9.8) по OZ оси с учётом связивектора
B магнитной индукции с вектором H напряжённостимагнитного поля (7.127) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" B = μ0 μH, имеет следующий вид: HM = (1/4πrv)pZQ′′[t - (r/v)]sinθeφ .(9.80)
|
 выражение для вектора E напряжённости электрическогополяэлектромагнитнойволны имеет следующий вид: E = H (μ0μ/ε0ε)1/2
выражение для вектора E напряжённости электрическогополяэлектромагнитнойволны имеет следующий вид: E = H (μ0μ/ε0ε)1/2
v = 1/(εε0μμ0)1/2↔ (μ0μ)1/2 = 1/v(ε0ε)1/2 ↔ E = H/vε0ε ↔ E = (1/4πεε0rv2) pZQ′′[t - (r/v)]sinθeθ.(9.81)
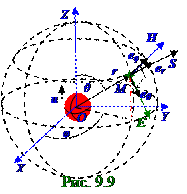
где (рис. 9.9) eθ-орт в сферической системе координат, направленный по касательной в M точке к координатной линии, представляющей собой окружность, вдоль которой меняетсяθ уголполярного расстояния в сферической системе координат; вектор H напряжённостимагнитногополя направлен по eφ орту φ угла долготы; вектор SПойнтинганаправлен по er орту r радиуса-вектора, поэтому вектор E напряжённостиэлектрическогополя, составляющий правовинтовуюсистему с векторами H, S, направленпо eθортуθ углаполярного расстояния.
ВекторD смещенияэлектрического поляэлектромагнитнойволны в произвольной M точке пространства, возникающего вследствие движения Q заряда (рис.9.9) по OZ оси с учётом выражения (5.87) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля", связывающихвектор D электрического смещенияс вектором E напряжённости электрическогополя D = ε0εE, имеет с учетом (9.81) следующий вид: D = (1/4πrv2) pZQ′′[t - (r/v)]sinθeθ.(9.82)
Вектор (9.80) H напряжённостимагнитного поля электромагнитнойволны в произвольной
M точке пространства, возникающего вследствие движения Q заряда (рис.9.9) по OZ оси, имеет следующую проекциюHφ на направление eφ орта в сферической системе координат:
Hφ= (1/4πrv) pZQ′′[t - (r/v)]sinθ,(9.83)
где pZQ′′[t - (r/v)] - проекция на OZ ось второй производной по tвремени вектора pQдипольногоэлектрического момента Q заряда, двигающегося по OZ оси, учитывающая величину Q[t - (r/v)] заряда шара V объёмом, который был раньше данного момента t временина величину τ = r/vвременного запаздывания, за которое электромагнитнаяволна с v = 1/(ε0εμ0μ)1/2 фазовой скоростьюраспространится от этого заряженного шара V объёмом до M точки, в которой определяется вектор
B индукциимагнитногополя.
ПроекцияHrна направление er орта равна нулю, т.к. вектор SПойнтинганаправленпоer орту. Векторы E, H напряжённостей электрическогои магнитногополя электромагнитнойволны согласно (9.39) S = [EH] образуют с направлениемвектора SПойнтингаправовинтовуюсистему, т.е. эти векторы E, H напряжённостей электрическогои магнитногополя электромагнитнойволны перпендикулярны er орту и, следовательно, вектору SПойнтинга.
ПроекцияHθна направление eθ вектора H напряжённостимагнитного поля электромагнитнойволны в произвольной M точке пространства, возникающего вследствие движения Q заряда
(рис.9.9) по OZ оси, равна нулю, т.к. этот вектор H напряжённостимагнитного поля электромагнитнойволныперпендикулярен eθ орту в сферической системе координат.
ПроекцииHθ, Hrна направление соответственно eθ, er ортов в сферической системе координат вектора H напряжённостимагнитного поля электромагнитнойволны в произвольной M точке пространства, возникающего вследствие движения Q заряда (рис.9.9) по OZ оси, имеют следующий вид: Hθ = 0; Hr= 0.(9.84) Векторы (рис.9.9) E, H напряжённостей электрическогои магнитногополя электромагнитнойволны согласно (9.39) S = [EH] образуют с направлениемвектора SПойнтинга правовинтовуюсистему, поэтому вектор E напряжённости электрическогополя электромагнитнойволны перпендикулярен eφ орту, по которому направлен вектор H напряжённости магнитного поля электромагнитнойволны, т.е. этот вектор E напряжённости электрическогополя электромагнитнойволны направлен по eθ орту и имеет в сферической системе координат только одну отличную от нуляEθ проекцию, имеющую следующий вид: Eθ = (1/4πεε0rv2)pZQ′′[t - (r/v)]sinθ, (9.85)
где при выводе Eθ проекции вектора E напряжённости электрическогополя электромагнитнойволны использовано соотношение (9.28) Em/Hm = (μ0μ/ε0ε)1/2амплитуд Em, Hm колебаний векторов напряжённостейсоответственно E электрическогои H магнитногополя электромагнитнойволны, а также использовано выражение (9.10) фазовой скоростиv = 1/(εε0μμ0)1/2 электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями.
ПроекцииEφ, Erна направление соответственно eθ, er ортов в сферической системе координат вектора E напряжённости электрическогополя электромагнитнойволны в произвольной M точке пространства, возникающего вследствие движения Q заряда (рис.9.9) по OZ оси, имеют следующий вид: Eφ= 0; Er= 0.(9.86)
Согласно (9.85), (9.83) численные значения модулей E, H соответственно векторов (рис.9.9)
E, H напряжённостей электрическогои магнитногополя электромагнитнойволны обратно пропорциональны r расстоянию до M точки, в которой определяется поле электромагнитнойволны. В направлении движения Q заряда по OZ оси, т.е. когда полярный θ угол равен нулю, эти E, H модули соответственно векторов E, H напряжённостей электрическогои магнитногополя электромагнитнойволны равны нулю.
Дипольный излучатель электромагнитных волнГерца. Интенсивность излучения диполя Герца
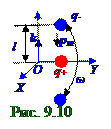
Простейшей системой, излучающей электромагнитныеволны, является колеблющийся электрический диполь. Это (рис.9.10) неподвижный положительный q+ точечный заряди колеблющийся около него с ωциклическойчастотой по аналогии с (1.19) из раздела 1.0 «Физические основы механики»q- отрицательныйзаряд. Вектор p дипольного электрического момента такой системы будет зависеть отt временисогласно следующему уравнению с гармонической функцией: p = pmcosωt,(9.87)
где pm = - qlm k - амплитудноезначение векторапо аналогии с (5.61) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля"электрического моментадиполяс расстоянием lm между зарядами q+ и q- в начальный момент времени t0 = 0 с учётом выбранного направления OZ оси координат и направления вектора p дипольного электрического моментаэтого диполя; k – единичный вектор. Проекция pZQ′′ на OZ ось вектора второй p′′(t) производной по tвремениот вектора (9.87) p дипольногоэлектрического момента, применяющаяся в (9.83), (9.85) для определения проекций Eθ,Hφ, на направление соответственно eφ, eθ ортов в сферической системе координат векторов (рис. 09.0.9)
E, H напряжённостей электрическогои магнитногополя электромагнитнойволны в произвольной
M точке пространства, имеет следующий вид: pZQ′′(t) = - ω2pZmcosωt, (9.88)
|
|
электромагнитнойволны в произвольной M точке пространства в данный момент t времени, вызванного колеблющимся с циклической ωчастотой (рис.9.10) по OZ оси координат электрическим диполем: Eθ = - (ω2pZmsinθ /4πεε0rv2)cos[ωt - (2πr/λ)], (9.89)
Hφ= -(ω2pZm sinθ /4πrv)cos[ωt - (2πr/λ)],(9.90)
где (2πr/λ) - отставание по аналогии (2.69) из раздела 2.0 "Колебания и волны" фазового угла электромагнитнойволны с λ длиной волны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями в зависимости от r расстояние до M точки, в которой определяется поле электромагнитнойволны, от фазовогоωtугла колеблющегося электрического диполявданныймомент t времени.
Амплитуды (9.89) Eθm = ω2pZmsinθ /4πεε0rv2,(9.90) Hφm= ω2pZmsinθ /4πrvвекторов
Eи H напряжённостейсоответственно электрического и магнитногополей уменьшаются при удалениина расстояние rот центра электрического диполя или возбудителя электромагнитнойволны и кроме этого зависят (рис.9.9) от полярного θ расстояния, т.е. θ угла между направлением
r радиуса- вектораи осью электрического диполя, находящейся на OZ оси координат, поэтому имеет место следующее соотношение: Eθm, Hφm ~ (1/r)sinθ. (9.91)
|
Δt <S> = ∫{[Eθm Hφm cos2[ωt - (2πr/λ)]/Δt}dt ~ EθmHφm ~ (1/r2)sin2θ,(9.92) 0
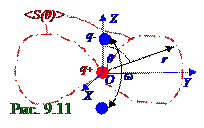
где <S> называют интенсивностью электромагнитнойволны при излучении диполем Герца. Зависимость <S (θ) > интенсивности электромагнитнойволны от θ угла между направлением
r радиуса- вектора(рис.9.11) и осью электрического диполя, находящейся на OZ оси координат,
называют диаграммой направленности. Сильнее всего излучает электрический дипольв направлениях, перпендикулярныхк егооси, находящейся на OZ оси координат, т.е. при θ = π/2. В направлениях, совпадающих (рис.9.11) с осью электрического диполя, находящейся на OZ оси координат, т.е. при θ = 0 или π, электрический дипольне излучает.
Средняя мощность электромагнитной волны, излучаемой движущимся с ускорением или колеблющимся точечным зарядом
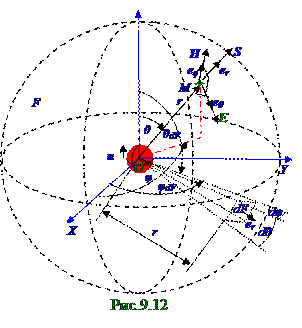
Вектор (9.39) SПойнтинга, модуль S которого, т.е. количествоэнергии, переносимое электромагнитнойволной через поверхность, перпендикулярную направлению распространения электромагнитнойволны и равной единичнойплощади за единицу t времениив данный момент этого t времени от движущегося (рис.9.12) по OZ оси Q заряда, с учётом (9.83), (9.85) направления векторов E, H напряжённостей электрическогои магнитногополяэлектромагнитнойволны в произвольной M точке пространства по направлению соответственно eθ, eφ ортов в сферической системе координат имеет следующий вид:
S = [E, H] =[Eθeθ, Hφeφ] = [eθ(1/4πεε0rv2)pQ′′[t - (r/v)]sinθ, eφ(1/4πrv)pQ′′[t - (r/v)]sinθ] == (pQ′′sinθ/4πr)2(1/εε0v3) er, (9.93)
где pQ′′ = |pZQ′′| - модуль второй производной по tвремениот вектора (9.74) pQдипольногоэлектрического момента Q заряда, который равен модулю проекции |pZQ′′| на OZ ось второй производной по tвремени вектора pQдипольногоэлектрического момента Q заряда, поскольку этот Q заряд двигается только по OZ оси; er -орт в сферической системе координат, направленный по r радиусу-вектору ,направленного в произвольную M точку пространства, в которой определяется поле электромагнитнойволны, и совпадающий по направлению с вектором SПойнтинга.
Орт (рис.9.12) erв сферической системе координати орты eθ, eφ образуют правовинтовуюсистему, поэтому имеет место следующее выражение: er = [eθ, eφ]. (9.94)Мощность(рис.9.12) P излучения, т.е. количествоэнергии, переносимой электромагнитнойволной за единицу времени в данный момент t времени через всю сферическуюповерхность F площадью, с учётом направления вектора SПойнтинга электромагнитнойволны по (9.93) er орту и перпендикулярности этого вектора SПойнтинга элементарной dF площадки в сферической системе координат, равна (9.47) следующему потоку Ф вектора SПойнтинга через эту сферическуюповерхность F площадью: P = Ф = ∫SdF= ∫er(pQ′′sinθdF/4πr)2(1/εε0v 3)err2sinθdF dθ dφ =
F F
π 2π π 2π
= [(pQ′′)2/16π2εε0v3] ∫sin3θdFdθ ∫dφ = - [(pQ′′)2/16π2εε0v3] ∫(1 - cos2θdF)dcosθdF ∫dφ =
0 0 0 0
π π
= - [(pQ′′)2/16π2εε0v3][(cosθdF)| - (cos3θdF/3)|]2π = - [(pQ′′)2/16π2εε0v3][-2 - (-2/3)]2π = 0 0
= - [(pQ′′)2/8πεε0v3](- 4/3) = (pQ′′)2/6πεε0v3, (9.95)
|
|
т.е. количествоэнергии, переносимой электромагнитнойволной через всю сферическую поверхность F площадью за единицу времени в данный момент t времени при (9.74) равенстве нулю модуля a = d2y/dt2 вектора a ускорения движения Q заряда, равна нулю.
Однако это не выполняется при движении зарядов с релятивистскимискоростями, что наблюдается в эффекте Вавилова - Черенкова.
Мощность(рис.9.12) P излучения, т.е. количествоэнергии, переносимой электромагнитнойволной за единицувремени в данный момент t времени через всю сферическую поверхность F площадью, вызванное колеблющимся с ωциклическойчастотой (рис.9.10) по
OZ оси координат электрическим диполем, определяется подстановкой (9.89), (9.90) проекцийEθ, Hφ на направление соответственно eφ, eθ ортов в сферической системе координат векторов E, H напряжённостей электрическогои магнитногополя электромагнитнойволны в произвольной
M точке пространства в (9.95), вследствие чего выражение Pмощностиизлучения колеблющимся с
ωциклическойчастотой электрическим диполем имеет следующий вид:
P = Ф = ∫SdF=
F
∫[eθ [-(ω2pZmsinθ /4πεε0rv2)cos[ωt -(2πr/λ)], eφ [-(ω2pZm sinθ /4πrv) cos [ωt -(2πr/λ)]]err2sinθdF dθ dφ =
F
= ∫[er[(ω4pZm 2sin2θ/16π2εε0 r2v3)cos2[ωt - (2πr/λ)]err2sinθdF dθ dφ =
F
π 2π
= (ω4pZm 2cos2[ωt - (2πr/λ)]/16π2εε0 v3) ∫sin3θdFdθ ∫dφ = ω4pZm 2cos2[ωt - (2πr/λ)]/6πεε0v3. (9.97) 0 0
Среднее значение <P> (рис. 9.12) мощности P излучения, т.е. количествоэнергии, переносимой в среднем за Δt интервалвремени электромагнитнойволной через всю сферическую поверхность F площадью r радиуса, вызванное колеблющимся с ωциклическойчастотой электрическим диполем в волновойзоне этого электрического диполя, т.е. с r радиусом сферической поверхности F площадьюмного большим (рис.9.10) расстояния lm между зарядами q+ и q-, которые они имеют в начальный t0 = 0 момент времени, с учётом (9.97) имеет следующий вид:
Δt <Р> = ∫{ω4pZm 2cos2[ωt - (2πr/λ)]/6πεε0v3}dt/Δt = ω4pm 2/12πεε0v3. (9.98)
0
Согласно (9.98)среднее значение <P>мощностиP излучения пропорционально четвёртойстепени ωциклическойчастоты колебаний электрическогодиполя, поэтому для эффективного излучения электромагнитныхволн используют источники в высокочастотном диапазоне спектра электромагнитного излучения.
Явления отражения и прохождения электромагнитной волны на плоской границе раздела двух сред. Закон Снеллиуса. Скин - эффект для плоской электромагнитной волны
|
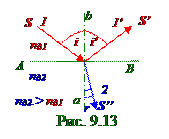
среду с nд2 показателем преломления, электромагнитная волначастично отражается и имеет направление вектора S′ плотности потока энергии или векторПойнтинга, совпадающее с 1′ лучом, а такжечастично преломляется и имеет направление вектора S′′ плотности потока энергии или векторПойнтинга, совпадающее с 2 лучом . В среде с nд1 показателем преломленияна падающиевекторыE0и H0 напряжённостейсоответственно электрического и магнитногополей накладываютсяотражённыевекторыEотри Hотр напряжённостейсоответственно электрического и магнитногополей электромагнитной волны. В среде с nд2 показателем преломленияимеются только преломлённыевекторыEпр, Hпр напряжённостейсоответственно электрического и магнитногополей.
Падающие E0, H0, отражённые Eотр, Hотри преломлённые Eпр, Hпр векторынапряжённостейсоответственно электрического и магнитногополей электромагнитной волныимеют векторы тангенциальныхсоставляющих E0τ, H τ0,E τотр, H τотр, E τпр, H τпр, которые параллельны AB границе,и векторы нормальныхсоставляющих E n0, H n0 ,E nотр, H nотр , E nпр, H nпр, которые перпендикулярны AB границе.
Согласно (5.90) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" при переходе вектора
E напряжённости электрическогополя через границу диэлектриков с различными диэлектрическимипроницаемостями ε1 и ε2 при отсутствии на этой границе свободныхq зарядов вектортангенциальных Eτсоставляющих напряжённости E электрическогополя не меняется. С учётом наличия в среде с nд1 показателем преломлениявекторов падающих E0τ и отражённых E τотр тангенциальныхсоставляющих вектора E1 напряжённостиэлектрического поля электромагнитной волны, а также с учётом существования в среде с nд2 показателем преломлениятолько вектора преломлённой E τпр тангенциальнойсоставляющей вектора E2 напряжённостиэлектрического поля выражение (5.90) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" для связи тангенциальныхсоставляющих Eτ векторов E1 и E2 напряжённости электрическогополяэлектромагнитной волнына границе раздела двух диэлектриков принимает следующий вид: E0τ + E τотр =E τпр.(9.100) Согласно (7.132) из раздела 7.2 "Магнитное поле в веществе" векторы тангенциальных H1τ и H2τ составляющихнапряжённости H магнитного поля на границе магнетиковсμ1 и μ2 магнитными проницаемостями сохраняют своё направлениеи модульпри условии отсутствиявектора
j плотности макроскопических или токов проводимостина поверхностигранице раздела этих магнетиков. Это справедливо в электромагнитной волне длявекторовпадающих H0τ и отражённых H τотр тангенциальныхсоставляющих вектора H1 напряжённостимагнитногополя в среде с nд1 показателем преломленияивекторомпреломлённой H τпр тангенциальнойсоставляющей вектора H2 напряжённостимагнитногополя в среде с nд2показателемпреломления, вследствие чего выражение (7.132) из раздела 7.2 "Магнитное поле в веществе" для связи Нτ тангенциальныхсоставляющих векторов H1 и H2 напряжённости магнитногополяэлектромагнитной волнына границе раздела двух магнетиков принимает следующий вид: H0τ + H τотр =H τпр .(9.101) Согласно (5.94) из раздела 5.2 " Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" при переходе через границу диэлектриков с различными диэлектрическимипроницаемостями ε1 и ε2 при отсутствии на этой границе свободных
q зарядов вектор нормальной Enсоставляющей вектораE напряжённости электрическогополя претерпевает разрыв. Это справедливо в электромагнитной волне длявекторовE n0, E nотр падающих, отражённых нормальныхсоставляющих векторовE1 напряжённостей электрическогополя в среде с nд1показателем преломления,ивектораE nпр преломлённойнормальнойсоставляющейвекторовE2 напряжённости электрическогополя в с
Дата добавления: 2016-02-14; просмотров: 923;
