Векторы. Основные операции над векторами.
| A(x1;y1) |
| y |
| x |
| y2 |
| y1 |
| x2 |
| x1 |
| B(x2;y2) |
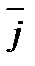
|
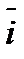
|
| Рис. 1.4 |
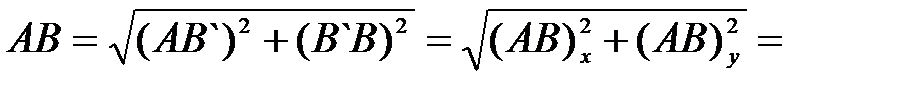
 , где (АВ)х и (АВ)у – проекции отрезка АВ на соответствующие оси. Эта величина определена своим численным
, где (АВ)х и (АВ)у – проекции отрезка АВ на соответствующие оси. Эта величина определена своим численным
значением и называется скалярной.

|
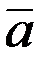
|
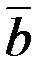
|
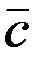
|
| Рис. 1.5 |
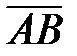 `точки А и В – начало и конец вектора) и характеризуют двумя параметрами: модулем (длиной) (обозначается |
`точки А и В – начало и конец вектора) и характеризуют двумя параметрами: модулем (длиной) (обозначается | 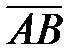 | = АВ) и направлением. Вектор, который без изменения длины и направления можно перенести в любую точку пространства, называют свободным. (В предлагаемом курсе рассматриваются эти векторы). Вектор удобнее обозначать `а, `b и т.д. Векторы `а и`b равны (`а =`b), если совпадают их длины | а |= |`b| или а = b) и направления. Если модули равны, а направления противоположны, векторы отличаются знаком т.е.
| = АВ) и направлением. Вектор, который без изменения длины и направления можно перенести в любую точку пространства, называют свободным. (В предлагаемом курсе рассматриваются эти векторы). Вектор удобнее обозначать `а, `b и т.д. Векторы `а и`b равны (`а =`b), если совпадают их длины | а |= |`b| или а = b) и направления. Если модули равны, а направления противоположны, векторы отличаются знаком т.е. 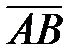 = –
= – 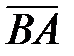 . Суммой векторов `а и`b называют вектор `с =`а +`b, определяемый (рис.1.5) по правилу треугольника: начало `b совмещают с концом `а , `с соединяет начало `а с концом`b. (
. Суммой векторов `а и`b называют вектор `с =`а +`b, определяемый (рис.1.5) по правилу треугольника: начало `b совмещают с концом `а , `с соединяет начало `а с концом`b. (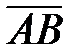 =
= 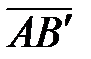 +
+ 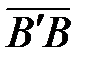 на рис 1.5). Произведением вектора `а на скаляр l (lÎR) называют вектор l `а, длина которого равна |l`a| = |`a| |l|. Если положить l = 1/а получим `a / a =`a0 – вектор единичной длины, имеющий тоже направление, что и `a (единичный вектор). При l = 0 получим `a × 0 =`0 (нуль вектор).
на рис 1.5). Произведением вектора `а на скаляр l (lÎR) называют вектор l `а, длина которого равна |l`a| = |`a| |l|. Если положить l = 1/а получим `a / a =`a0 – вектор единичной длины, имеющий тоже направление, что и `a (единичный вектор). При l = 0 получим `a × 0 =`0 (нуль вектор).
Операции сложения векторов и умножения вектора на скаляр называют линейными.
Сумму вида 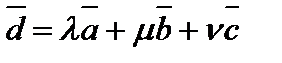 , где
, где 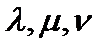 -скаляры, называют линейной комбинацией векторов
-скаляры, называют линейной комбинацией векторов 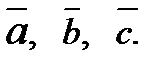 (Или говорят, что вектор
(Или говорят, что вектор 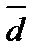 линейно выражается через
линейно выражается через 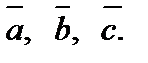 ) Векторы называют линейно независимыми, если ни один из них не выражается линейно через другие (не может быть представлен их линейной комбинацией). Формальное определение таково: векторы а1, а2, …, аn называют линейно – зависимыми, если l1`а1 + l2`а2 +…+ln`аn = 0 (1.15),
) Векторы называют линейно независимыми, если ни один из них не выражается линейно через другие (не может быть представлен их линейной комбинацией). Формальное определение таково: векторы а1, а2, …, аn называют линейно – зависимыми, если l1`а1 + l2`а2 +…+ln`аn = 0 (1.15),
где l1, l2, …, ln – числа, хотя бы одно из которых отлично от нуля. В этом случае один из векторов может быть представлен в виде линейной комбинации остальных векторов.
Если соотношение (1.15) выполняется только в случае, когда l1 = l2 =… = ln = 0,то`а1,`а2, …,`аn линейно независимы.
Вернемся к рис.1.4. Зададим направления осей Ох и Оу единичными векторами `iи`jсоответственно. Очевидно, что 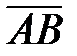 =
= 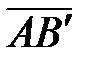 +
+ 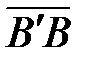 . Но очевидно также, что
. Но очевидно также, что 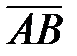 = `i ×АВ` = `i × (АВ)хи
= `i ×АВ` = `i × (АВ)хи 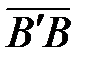 = `j × В`B = `j × (АВ)у. Таким образом вектор `a в двумерных декартовых координатах можно представить в виде: `a = `i ax + `j ay (
= `j × В`B = `j × (АВ)у. Таким образом вектор `a в двумерных декартовых координатах можно представить в виде: `a = `i ax + `j ay (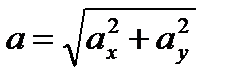 ) а в трехмерных `a = `i ax + `j ay + `каz, где ах, ау, аz – проекции вектора`a на соответствующие оси,
) а в трехмерных `a = `i ax + `j ay + `каz, где ах, ау, аz – проекции вектора`a на соответствующие оси, 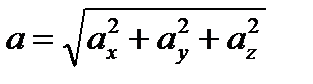 , а i,`j,`к – единичные векторы этих осей. Такое представление вектора называется разложением его по декартову ортонормированному базису. (Системе линейно независимых единичных векторов `i ,`j ,`к). (Базисом на плоскости называют любую упорядоченную пару `е1, `е2 линейно независимых векторов. Вектор `a на плоскости можно единственным образом разложить по базису, т.е. представить в виде `а = а1`е1 + а2`е2 (а1, а2 Î R), где а1 и а2 – координаты вектора `ав выбранном базисе (проекции вектора `а на соответствующие оси, направления которых заданы векторами`е1и`е2). Вектор в разложении по базису запишется в виде `а( а1, а2).
, а i,`j,`к – единичные векторы этих осей. Такое представление вектора называется разложением его по декартову ортонормированному базису. (Системе линейно независимых единичных векторов `i ,`j ,`к). (Базисом на плоскости называют любую упорядоченную пару `е1, `е2 линейно независимых векторов. Вектор `a на плоскости можно единственным образом разложить по базису, т.е. представить в виде `а = а1`е1 + а2`е2 (а1, а2 Î R), где а1 и а2 – координаты вектора `ав выбранном базисе (проекции вектора `а на соответствующие оси, направления которых заданы векторами`е1и`е2). Вектор в разложении по базису запишется в виде `а( а1, а2).
Аналогично определяется базис в трехмерном пространстве, где любой вектор можно представить в виде `а = а1`е1 + а2`е2 + а3`е3 или `а( а1, а2, а3), где а1, а2, а3 координаты вектора `ав базисе (`е1,`е2,`е3).
Ортонормированным называется базис взаимноперпендикулярных векторов единичной длины (ортов).
Направление `аопределяется углами a, b, gобразованными с осями Ох, Оу, Оzсоответственно. Направляющие косинусы вектора `а определяются выражениями: 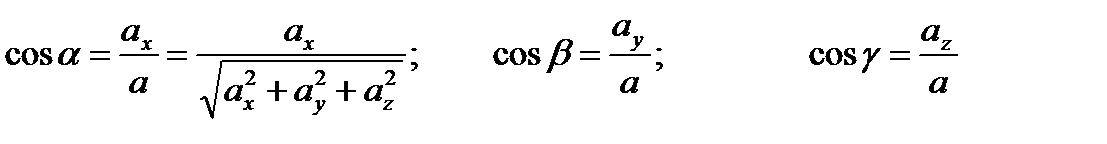 (1.16)
(1.16)
и связаны соотношением: cos2a + cos2b + cos2g = 1 (1.17).
Линейные операции над векторами, данными в разложении по декартову базису записывают так: `с = `а + `b = (ax + bx)`i +(ay + by)`j + (az + bz)`к(1.18)и `а l = ax li + ay lj + az lк(1.19)
Произвольной точке М (х, у, z) можно поставить в соответствие вектор `r,соединяющий начало координат с точкой М, называемый радиусом – вектором точкиМ и обозначаемый `r (М). Очевидно, что `r = `i x + `j y + `кz, где x, y, z координаты этой точки. Вектор 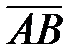 где А (x1, y1, z1) и В (x2, y2, z2) начало и конец вектора можно представить в виде
где А (x1, y1, z1) и В (x2, y2, z2) начало и конец вектора можно представить в виде 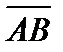 = `r2 – `r1.
= `r2 – `r1.
Контрольные вопросы.
1) Что называется вектором? Что называется модулем вектора?
2) Как определяется равенство векторов?
3) Как определяются операции сложения векторов и умножения вектора на скаляр (линейные операции над векторами)? Каковы их свойства?
4) Как определяются координаты вектора в пространстве?
5) Как выражаются модель вектора и его направляющие косинусы через координаты вектора?
6) Как выражаются координаты вектора через координаты точек, являющихся началом и концом этого вектора?
7) Напишите формулу для вычисления расстояния между двумя точками в пространстве.
8) Как производится сложение векторов и умножение вектора на скаляр (линейные операции над векторами), если векторы заданы своими координатами?
Тест 6.
1) Найдите координаты вектора 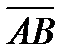 и его длину, если даны точки А(1,2,3) и В(3,-4,6) и укажите верный ответ:
и его длину, если даны точки А(1,2,3) и В(3,-4,6) и укажите верный ответ:
а) 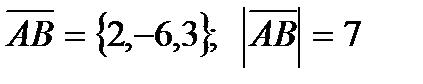
б) 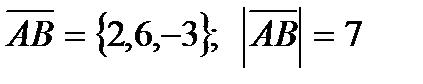
2) Построить параллелограмм на векторах 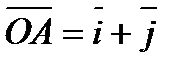 и
и 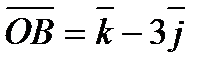 и определить его диагонали и указать верный ответ:
и определить его диагонали и указать верный ответ:
а) 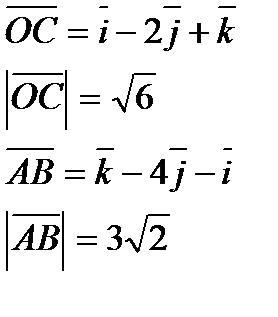 б)
б) 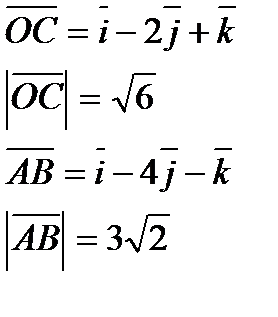
1.5.2. Скалярное произведение.Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла j между ними: `а ×`b= abcos j (1.20).
Свойства скалярного произведения:
1) `а ×`а = а2 (`а2 = а2)
2) `а ×`b = 0 если `а = 0, `b = 0, `а =`b = 0 или `а ^`b (j = p / 2)
3) `а ×`b =`b ×`а (переместительный закон)
4) `а (`b + `с) =`а`b +`а`с (распределительный закон)
5) (l`а)`b = `а(l`b) = l(`а`b) (сочетательный закон по отношению к
скалярному множителю).
Из 1) следует, что `i2 = `j 2 = `к2 =1, а из 2) что `i `j = `i `к =`j `к = 0 (единичные вектора ортогональны (взаимно-перпендикулярны)).
Если вектора `а и`b заданы своими координатами (проекциями на оси Ох, Оу, Оz), то `а`b = axbx + ayby + azbz (1.21).
Действительно, `а`b = (`i ax + `j ay + `к az) (`i bx + `j by + `к bz) = `i2 ax bx + `i `j ay bx + `к`i az bx + `i `j ax by +`j2 ay by + `к `j az by + `i `к ax bz + `j`кaybz + `к2 azbz = [мы уже знаем, что квадраты ортов равны 1, а попарные произведения – 0] =axbх + ayby + azbz.
Контрольные вопросы.
1) Что называется скалярным произведением векторов? Каковы его свойства и выражение через координаты векторов-сомножителей?
2) По какой формуле можно вычислить угол между двумя векторами?
Дата добавления: 2016-04-14; просмотров: 1230;
