Матрицы. Основные свойства и операции.
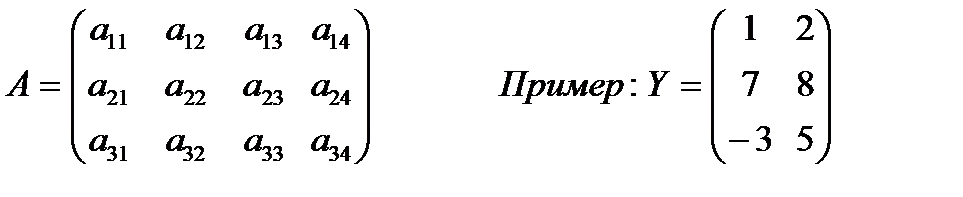 Матрицей называют прямоугольную таблицу, составленную из каких – либо математических объектов (элементов), в простейшем случае – из чисел. Принятое обозначение:
Матрицей называют прямоугольную таблицу, составленную из каких – либо математических объектов (элементов), в простейшем случае – из чисел. Принятое обозначение:
В общем случае числа строк m и столбцов n произвольны и определяют размер матрицы, обозначаемый (m 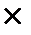 n). Если строка одна, А = (а11, а12, …, а1n) – матрица-строка; аналогично определяется матрица–столбец (размеры – (1
n). Если строка одна, А = (а11, а12, …, а1n) – матрица-строка; аналогично определяется матрица–столбец (размеры – (1 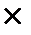 n) и (m
n) и (m 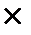 1) соответственно).
1) соответственно).
Если число строк равно числу столбцов – квадратная матрица порядка n. Квадратной матрице А соответствует определитель, обозначаемый DА (или DА). Если DА ¹ 0, матрица А называется невырожденной (неособой), если DА = 0, то А – вырожденная (особая) матрица.
Если в квадратной матрице А поменять местами столбцы и строки, то получим новую матрицу, обозначаемую А* и называемую траспонированной (сама операция замены называется траспонированием). Квадратная матрица, у которой все элементы (кроме, может быть, стоящих по главной диагонали, идущей из левого верхнего в правый нижний угол) равны нулю, называется диагональной. Такая матрица, если все диагональные элементы равны единице, называется единичной и обозначается буквой Е. Нулевой называют матрицу, все элементы которой равны нулю.
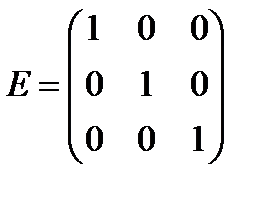
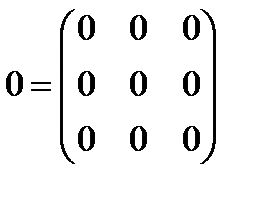
Квадратную матрицу, в которой аij = aji называют симметрической (такая матрица совпадает со своей транспонированной, т.е. А = А*).
Две матрицы А и В считаются равными (А = В) тогда и только тогда, когда равны их соответственные элементы, т.е.аmn = bmn.
Матрицы одинакового размера можно складывать, получая новую матрицу того же размера по формуле:
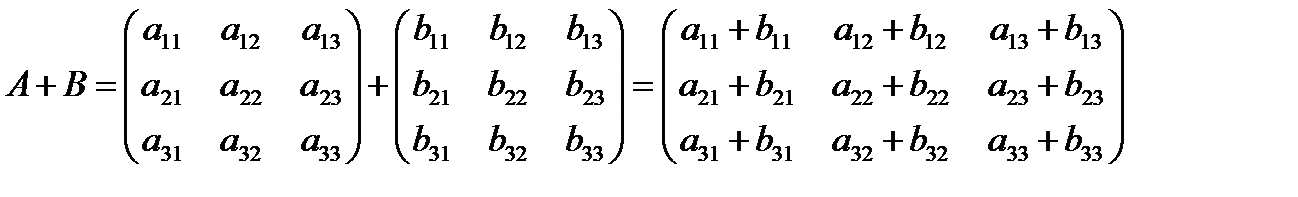 (1.11)
(1.11)
Произведением числа aна матрицу А называют матрицу определяемую
равенством: 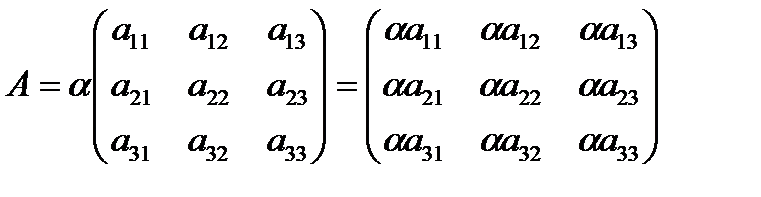 (1.12)
(1.12)
Умножение матриц возможно в том случае, если число столбцов умножаемой матрицы равно числу строк матрицы множителя. Размер матрицы-произведения определяется соотношением (m 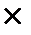 n)
n) 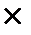 (n
(n 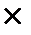 k)=(m
k)=(m 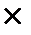 k). Произведение матриц А и В, обозначаемое АВ находят по правилу:
k). Произведение матриц А и В, обозначаемое АВ находят по правилу:
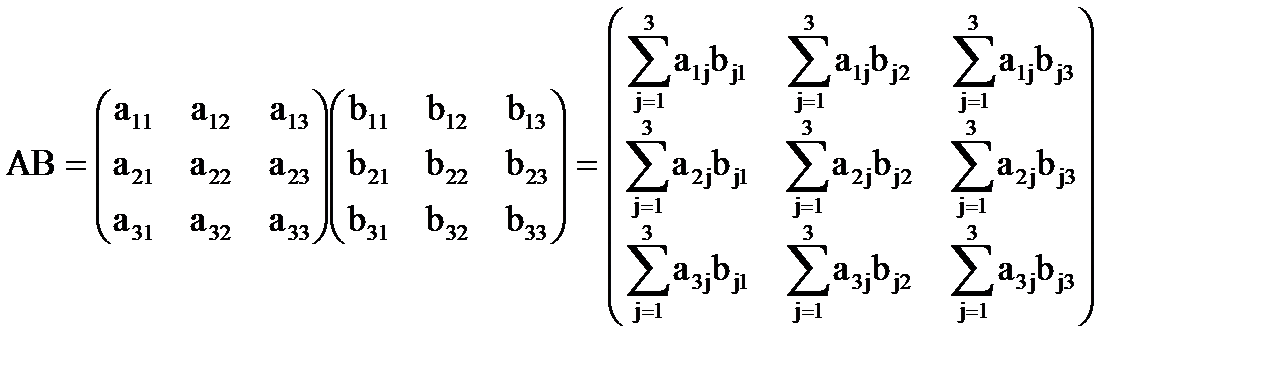 (1.13)
(1.13)
т.е. элемент матрицы – произведения, стоящий в i – й строке и к – ом столбце, равен сумме произведений соответственных элементов i – й строки матрицы А и к – ого столбца матрицы В. Пример:
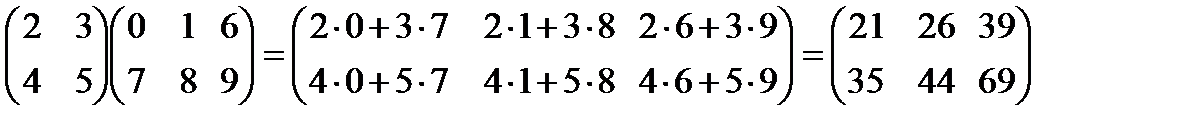
Отметим, что переместительный закон для произведения матриц в общем случае не выполняется: АВ ¹ ВА.
Аналогично понятию обратного числа (произведение числа на число обратное равно единице: а × а–1 = 1) вводится понятие обратной матрицы А–1.
А × А–1 = Е, где Е – единичная матрица.
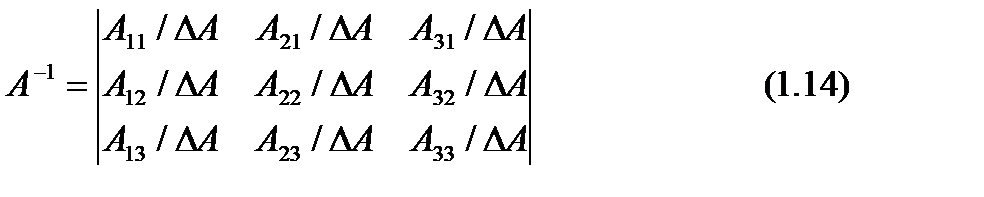 Обратную матрицу имеет всякая невырожденная квадратная матрица, причем:
Обратную матрицу имеет всякая невырожденная квадратная матрица, причем:
где Аmn – алгебраическое дополнение элемента матрицы аmn (см. (1.4.))
Альтернативный способ вычисления А-1 приведён в разделе (1.4.3)
Контрольные вопросы.
1) Что называется матрицей? Приведите примеры. 2) Какие действия установлены над матрицами? Как они определяются и каковы их основные свойства? 3) Какая матрица называется обратной для данной матрицы А? Для любой ли матрицы существует обратная? Если нет, то какому условию должна удовлетворять данная матрица, чтобы для неё существовала обратная матрица? Как найти обратную матрицу? Тест №3. Найти матрицу, обратную данной и указать верный ответ: а) 1.4.2. Решение уравнений.Определение операции умножения матриц позволяет предложить матричный способ решения системы линейных уравнений. Систему уравнений можно представить в матричной форме АХ = В, где Если DА ¹ 0, то решение системы запишется в виде Х = А–1В т.е. для нахождения матрицы – столбца неизвестных надо умножить обратную матрицу системы на матрицу-столбец свободных членов. Контрольные вопросы.
1) Что называется матрицей системы линейных уравнений и расширенной матрицей системы линейных уравнений? 2) Опишите матричный способ решения систем линейных уравнений Тест 4. Найти решение системы а) 1.4.3. Ранг матрицы.Пусть дана прямоугольная матрица А, содержащая m строк и n столбцов. Выделим в этой матрице произвольным образом к строк и к столбцов (к £ m, к £ n). Определитель к – ого порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных столбцов и строк, называется минором к – ого порядка матрицы А. Очевидно, что можно составить миноры любого порядка, не превышающего m и n, причем (в общем случае) по крайней мере некоторые из них не будут равны нулю. Рангом матрицы А называют наибольший порядок минора этой матрицы, отличного от нуля. (Если все элементы матрицы равны нулю, то и ранг ее принимают равным нулю). Отличные от нуля миноры, порядок которых равен рангу матрицы, называют базисными минорами. Ранг матрицы обозначают символом r(А). Если r(A) = r(B), то матрицы А и В называют эквивалентными (Символическая запись:А ~ В). Элементарные преобразования матрицы не изменяют ее ранга. Это можно использовать при вычислении ранга матрицы. Под элементарными преобразованиями понимают: 1. Замену строк столбцами, а столбцов – соответствующими строками; 2. Перестановку строк; 3. Вычеркивание строк, все элементы которых равны нулю; 4. Умножение какой – либо строки на отличное от нуля число; 5. Пример: Найти ранг матрицы Сложим соответствующие элементы 1 и 3 строк, а затем разделим на 4 элементы «обновленной» первой строки. Из элементов 1 строки вычтем соответствующие элементы 2 строки, после чего вычеркнем 1 строку. Следовательно и ранг исходной матрицы r(A) = 2. Можно показать, что ранг матрицы равен числу не обнуляемых элементарными преобразованиями строк. Примечание: Элементарные преобразования матриц позволяют упростить вычисление обратной матрицы. Припишем к матрице А единичную матрицу Е той же размерности, отделённую вертикальной чертой. Умножив обе части сдвоенной матрицы А|Eна А-1 получим Пример: А= Составим сдвоенную матрицу Проверка Контрольные вопросы.
Что называется рангом матрицы?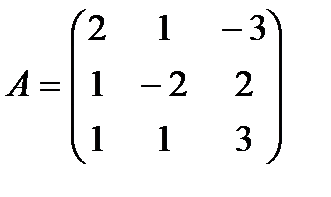
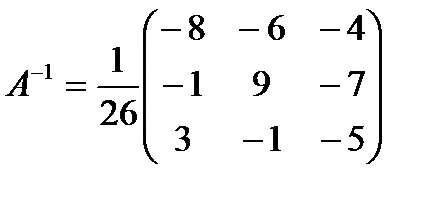 ; б)
; б) 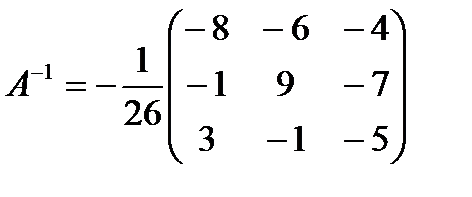
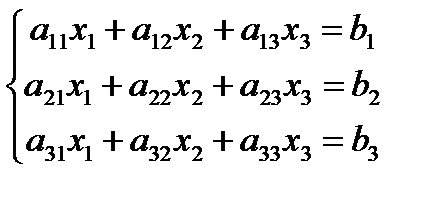
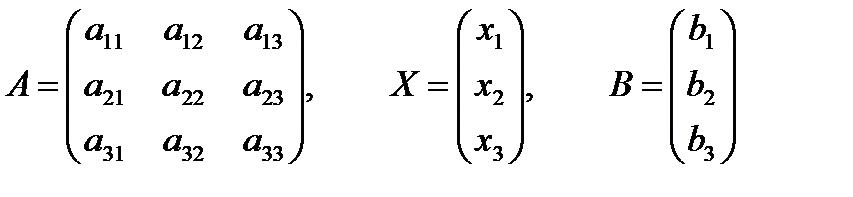
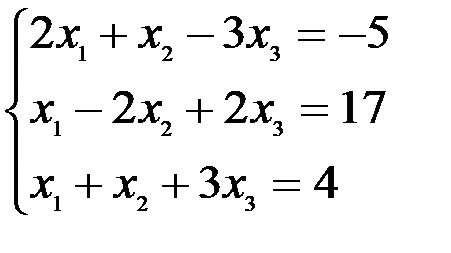 с помощью обратной матрицы
с помощью обратной матрицы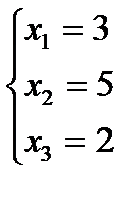 б)
б) 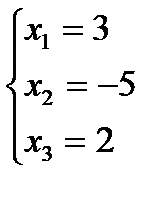
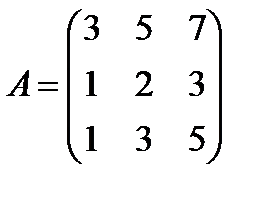 Прибавление к элементам одной строки соответствующих элементов другой строки.
Прибавление к элементам одной строки соответствующих элементов другой строки.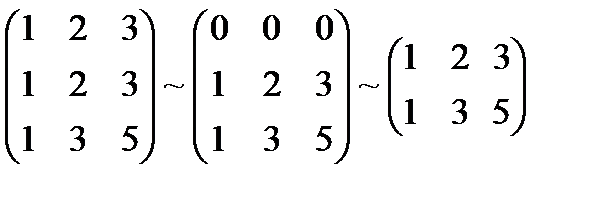
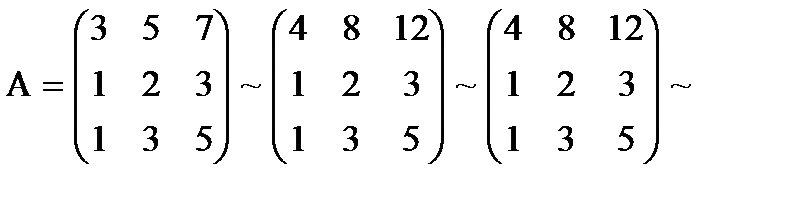
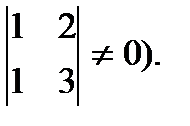
Ранг последней матрицы равен 2 (действительно,
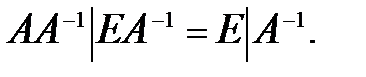 Таким образом, если элементарными преобразованиями сдвоенной матрицы левую часть её привести к виду Е, то в правой части окажется искомая обратная матрица А-1.
Таким образом, если элементарными преобразованиями сдвоенной матрицы левую часть её привести к виду Е, то в правой части окажется искомая обратная матрица А-1.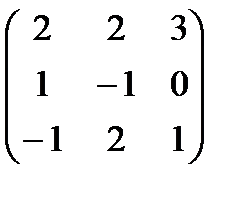 ; Найти А-1.
; Найти А-1.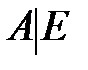 и преобразуем её.
и преобразуем её.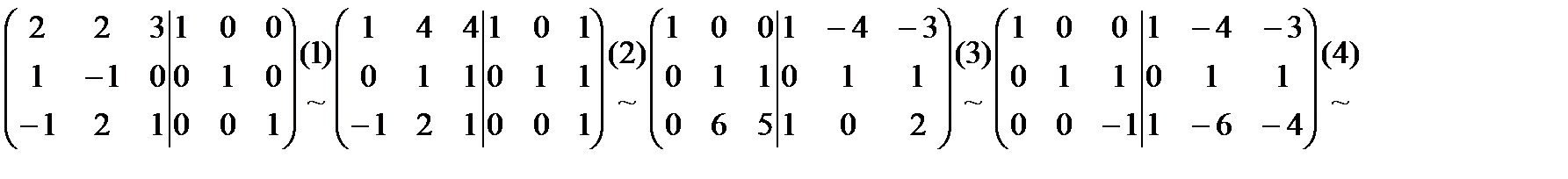
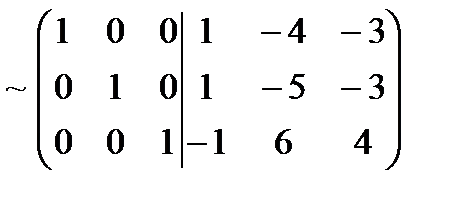 ;Т.о. А-1 =
;Т.о. А-1 = 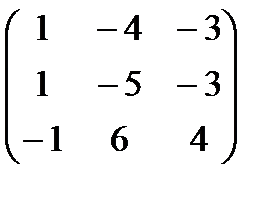 . В (1) преобразовании к 1 и 2 строкам прибавляем 3; во (2) прибавляем к 3 строке 1, а из 1 вычитаем 2, умноженную на 4; в (3) вычитаем из 3 строки 2, умноженную на 6; в (4) прибавляем к 2 строке 3, а 3 умножаем на -1.
. В (1) преобразовании к 1 и 2 строкам прибавляем 3; во (2) прибавляем к 3 строке 1, а из 1 вычитаем 2, умноженную на 4; в (3) вычитаем из 3 строки 2, умноженную на 6; в (4) прибавляем к 2 строке 3, а 3 умножаем на -1.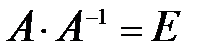 показывает, что А-1 найдена правильно.
показывает, что А-1 найдена правильно.
Дата добавления: 2016-04-14; просмотров: 3359;
