Аналитическая геометрия. Элементы линейной алгебры.
1.1.Координаты.Возьмем произвольную прямую, выберем единицу масштаба и положительное направление. Зафиксируем на прямой (принято называть такую прямую осью) произвольную точку О. Расстояние от нее до другой точки определится числом единиц длины в соответствующем отрезке.
| А2(-4) О(0) А1(5) -5 -4 -3 -2 -1 0 1 2 3 4 5 Рис. 1.1 |
| ρ |
| Рис. 1.2 Рис. 1.1 |
| y |
| yn |
| xn |
| x |
| O(0;0) |
| Mn(xn;yn))) |
| j |
Проекции точки Mn на оси Ох и Оу (точки xn и yn соответственно, рис. 1.2)
позволяют определить координаты точки Mn как числа, выражающие длины отрезков Oхn и Oуn (xn – абсцисса, yn – ордината точки Mn). Символически положение точки Mn с известными координатами xn и yn записывается в виде Mn(xn, yn),произвольной точки – М(x,y), где x и y – текущие координаты.
Рассмотрим еще одну систему координат на плоскости – полярную. Она определяется заданием точки О (полюса), полярной оси, проходящей через нее, и направлением отсчета угла j между полярной осью и отрезком, соединяющим полюс О с произвольной точкой М плоскости.
Полярными координатами точки М называют пару чисел r и j, где r – длина отрезка ОМ, а j – упомянутый угол в радианах.(Принятое направление отсчёта - против часовой стрелки от положительного направления оси.) Вернемся к рис. 1.2. Примем за полярную ось Oх. Для установления связи между декартовыми и полярными координатами точки Mn достаточно рассмотреть прямоугольный треугольник OMnхn. Легко видеть, что
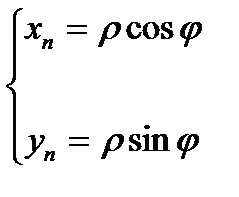 (1.1) Þ
(1.1) Þ 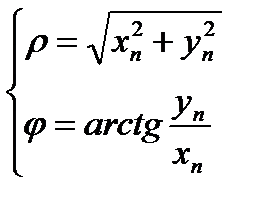 (1.2)
(1.2)
| z |
| zn |
| y |
| yn |
| xn |
| x |
| • mn(xn;yn;zn) |
| Рис. 1.3 |
Аналогично тому, как это делалось для плоскости, вводятся декартовы координаты в трехмерном пространстве R3. Задается единица масштаба и три взаимно перпендикулярные оси Oх, Oу и Oz, пересекающиеся в точке О. Положение точки однозначно определяется тремя числами – абсциссой x, ординатой y и аппликатой z (рис. 1.3) (к осям (координатам) x и y «добавили» ось (координату) z).
Контрольные вопросы.
1) Как определяются декартовы координаты точки на плоскости?
2) Чем отличаются друг от друга декартовы координаты двух точек, симметричных относительно а) оси ОХ, б) оси ОУ, в) начала координат?
3) Напишите формулы преобразования координат а) при параллельном переносе системы координат; б) при повороте системы координат.
4) Какой вид примет формула, по которой определяется расстояние между двумя точками, если: а) точки имеют одинаковые ординаты, но различные абсциссы; б) точки имеют одинаковые абсциссы, но различные ординаты; в) одна из точек совпадает с началом координат?
5) Как определяется декартова прямоугольная система координат в пространстве? Как определяются координаты точки в пространстве?
1.2. Определители.Пусть дана квадратная (число строк равно числу столбцов) таблица (матрица) А из четырех элементов (чисел).
Назовем определителем второго порядка некоторое число D, соответствующее этой таблице и вычисляемое по правилу:
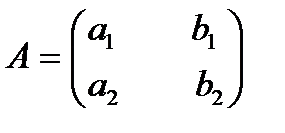 ;
; 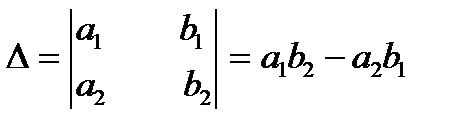 (1.3)
(1.3)
(Из произведения элементов, стоящих по главной диагонали вычитается произведение элементов, стоящих по вспомогательной диагонали).
Аналогично может быть составлен определитель произвольного (N-го) порядка, соответствующий квадратной матрице, содержащей N строк и N столбцов. Сформулируем алгоритм его вычисления на примере определителя третьего порядка (N=3).
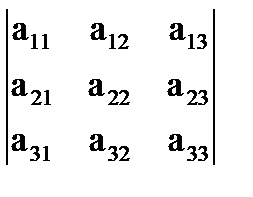
| Для нумерации элементов определителя использованы двойные индексы, позволяющие однозначно определить местоположение элемента: первое число индекса – это номер строки, а второе – номер столбца, на перекрестье которых |
расположен соответствующий элемент. (Строки и столбцы нумеруются сверху-вниз и справа-налево соответственно).
Пусть дан определитель N порядка. Минором Mmn элемента amn определителя (1 ≤ m ≤ N – номер строки, а 1 ≤ n ≤ N – номер столбца на перекрестьи которых элемент аmn расположен) назовем определитель N – 1 порядка, получаемый из исходного вычеркиванием m строки и n столбца. Алгебраическое дополнение элемента amn определим соотношением
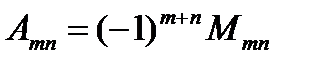 (1.4)
(1.4)
Операция вычисления определителя с помощью вновь введенных величин называется раскрытием определителя по элементам его строки (столбца) и выполняется в соответствии со следующей теоремой: Определитель произвольного порядка равен сумме произведений элементов любой его строки (или столбца) на их алгебраические дополнения. Несложно убедиться, что правило вычисления определителя второго порядка есть частный случай предложенного способа.
Определитель третьего порядка, раскрываемый по элементам первой строки, примет вид:
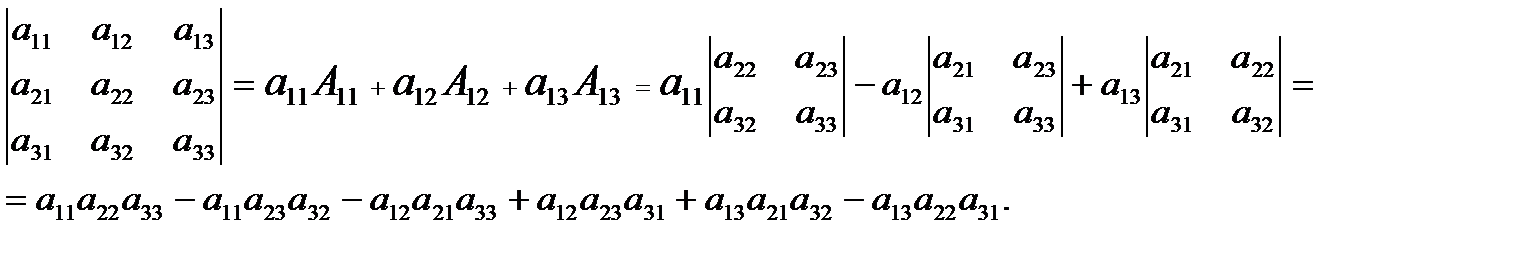 (1.5)
(1.5)
(Это соотношение известно как формула Саррюса.)
Полезно иметь ввиду следующие свойства определителей:
1. Определитель не изменится, если строки заменить столбцами, а столбцы строками.
2. Общий множитель элементов любой строки (столбца) можно вынести за знак определителя.
3. Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца), то определитель равен нулю.
4. Если все элементы некоторой строки (столбца) равны нулю, то определитель равен нулю.
5. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
6. Определитель не изменится, если к элементам одной строки (столбца), прибавить соответственные элементы другой строки (столбца) умноженные на одно и то же число.
7. 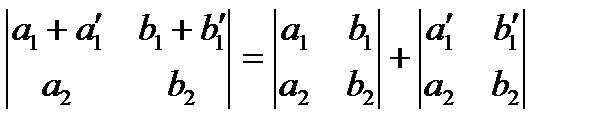
Контрольные вопросы.
1) Каковы основные свойства определителей?
2) Что называется минором и алгебраическим дополнением?
3) Каковы способы вычисления определителей?
Тест 1.
Вычислить определители и указать верный ответ
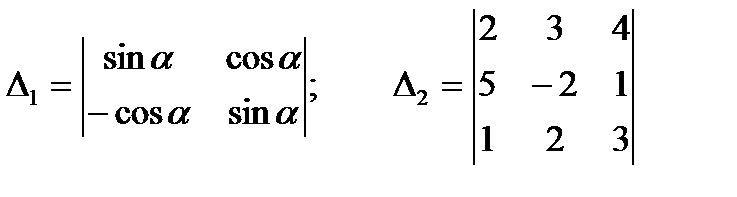
а) 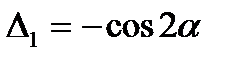
б) 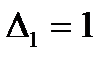
а) 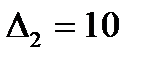
б) 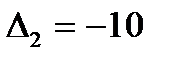
Дата добавления: 2016-04-14; просмотров: 1496;
