Аналитическая геометрия. Элементы векторной и линейной алгебры. Комплексные числа.
Основные теоретические сведения
1. Определителем 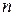 -го порядка называется число
-го порядка называется число 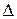 , записываемое в виде квадратичной таблицы
, записываемое в виде квадратичной таблицы
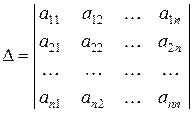
и вычисляемое, согласно указанному ниже правилу, по заданным числам 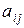 , которые называются элементами определителя. Индекс
, которые называются элементами определителя. Индекс 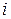 указывает номер строки, а
указывает номер строки, а 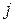 – номер столбца квадратной таблицы.
– номер столбца квадратной таблицы.
Минором 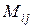 элемента
элемента 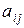 называется определитель
называется определитель 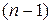 порядка, получаемый из определителя
порядка, получаемый из определителя 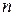 -го порядка, вычеркиванием
-го порядка, вычеркиванием 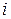 -й строки и
-й строки и 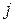 -го столбца.
-го столбца.
Алгебраическое дополнение 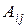 элемента
элемента 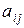 определяется равенством
определяется равенством
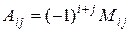 .
.
Рекуррентная формула для вычисления определителя 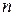 -го порядка имеет вид
-го порядка имеет вид
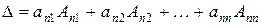
(разложение определителя по элементам 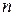 -й строки).
-й строки).
2. Скалярным произведением двух векторов 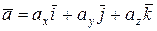 и
и 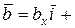
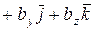 называется число, определяемое равенством
называется число, определяемое равенством
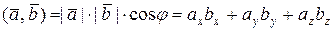 ,
,
где 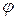 – угол между векторами
– угол между векторами 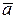 и
и 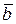 .
.
3. Векторным произведением векторов 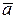 и
и 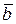 называется вектор
называется вектор 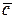 , обозначаемый
, обозначаемый 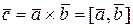 , который удовлетворяет условиям:
, который удовлетворяет условиям:
1) 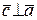 ,
, 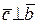 ;
;
2) 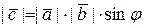 ;
;
3) 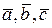 – правая тройка векторов;
– правая тройка векторов;
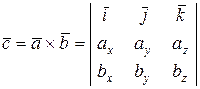
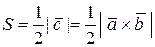 – формула для вычисления площади треугольника.
– формула для вычисления площади треугольника.
4. Смешанное произведение трех векторов 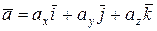 ,
, 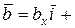
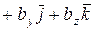 ,
, 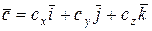 есть число, равное
есть число, равное
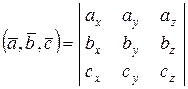 .
.
Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах.
5. Выражение вида 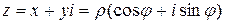 называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь
называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь 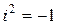 ,
, 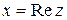 – действительная часть,
– действительная часть, 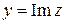 – мнимая часть комплексного числа
– мнимая часть комплексного числа 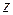 ;
; 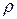 и
и 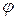 – модуль и аргумент числа
– модуль и аргумент числа 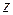 :
:
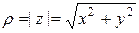 ;
; 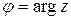
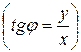 .
.
Извлечение корня 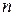 -ой степени (
-ой степени ( 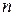 – натуральное число) из числа
– натуральное число) из числа 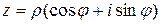 производится по формуле
производится по формуле
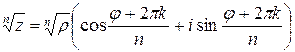 ,
,
где 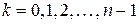 .
.
Пример 1.Дана система линейных алгебраических уравнений:
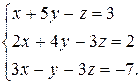
Проверить, совместна ли эта система, и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса; в) с помощью обратной матрицы. Совместность данной системы проверим по теореме Кронекера - Капелли.
Решение. С помощью элементарных преобразований найдем ранг матрицы
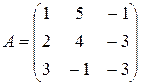
данной системы и ранг расширенной матрицы
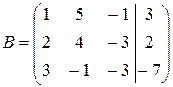
Для этого умножим первую строку матрицы В на –2 и сложим со второй, затем умножим первую строку на –3 и сложим с третьей, получим
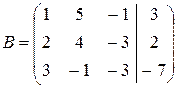 ~
~ 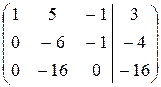 ~
~ 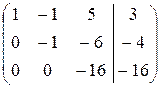 .
.
Следовательно, rang A = rang B = 3 (числу неизвестных), исходная система имеет единственное решение.
а) Находим решение системы по формулам Крамера
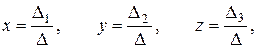
где
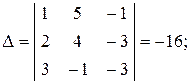
| 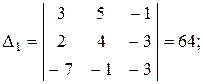
| |
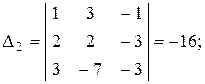
| 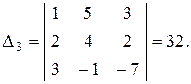
|
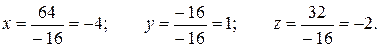
б) Метод Гаусса. Составим расширенную матрицу и проведем необходимые элементарные преобразования. Элементы первой строки умножим на –2 и прибавим к соответствующим элементам 2-ой строки, затем элементы первой строки умножим на –3 и прибавим к соответствующим элементам третьей строки.
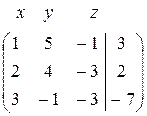 ~
~ 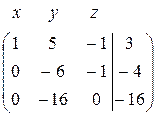 ~
~ 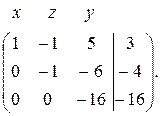
Последней матрицей соответствует система, эквивалентная исходной:
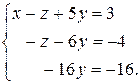
Из этой системы, двигаясь снизу вверх, последовательно находим:
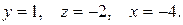
в) Матричный метод. Так как det A = -16 ¹0, то матрица А невырожденная, существует обратная матрица А-1, определяемая по формуле:
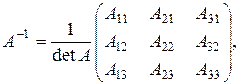
где 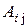
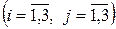 являются алгебраическими дополнениями соответствующих элементов матрицы А.
являются алгебраическими дополнениями соответствующих элементов матрицы А.
Введем в рассмотрение матрицы столбцы для неизвестных и свободных членов:
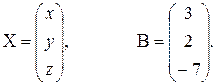
Тогда данную систему можно записать в матричной форме: 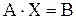 , отсюда находим
, отсюда находим 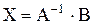 - решение системы в матричной форме.
- решение системы в матричной форме.
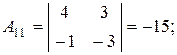
| 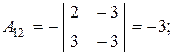
|
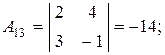
| 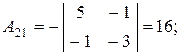
|
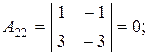
| 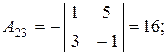
|
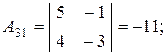
| 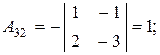
|
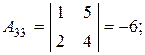
|
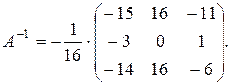
Решение системы:
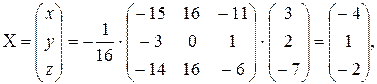
таким образом,
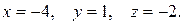
Пример 2.Составить канонические уравнения: а) эллипса, большая ось которого равна 5, а фокус находится в точке F(3,0); б) гиперболы с мнимой осью в=3 и 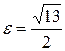 ; в) параболы, имеющей директрису x=-3.
; в) параболы, имеющей директрису x=-3.
а) Каноническое уравнение эллипса имеет вид 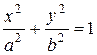 . По условию задачи большая полуось а=5, с=3. Для эллипса выполняется равенство
. По условию задачи большая полуось а=5, с=3. Для эллипса выполняется равенство 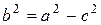 . Подставив значения а и с, найдем в2=16. Искомое уравнение эллипса:
. Подставив значения а и с, найдем в2=16. Искомое уравнение эллипса:
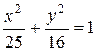 .
.
б) Каноническое уравнение гиперболы имеет вид 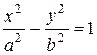 . По условию задачи мнимая полуось в=3, эксцентриситет
. По условию задачи мнимая полуось в=3, эксцентриситет 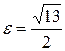 . Для гиперболы справедливо равенство
. Для гиперболы справедливо равенство 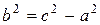 и учитывая, что
и учитывая, что 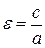 , находим а2 = 16. Искомое уравнение гиперболы:
, находим а2 = 16. Искомое уравнение гиперболы:
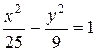 .
.
в) Каноническое уравнение параболы в данном случае имеет вид y2=2px, а уравнение ее директрисы 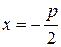 . По условию x=-3, следовательно,
. По условию x=-3, следовательно, 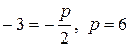 , уравнение параболы имеет вид
, уравнение параболы имеет вид 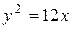 .
.
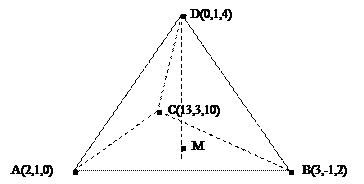 Пример 3.Даны координаты вершин пирамиды ABCD: A(2,1,0), B(3,-1,2), C(13,3,10), D(0,1,4). Найти: 1) угол между ребрами AB и AD; 2) уравнение плоскости АВС; 3) угол между ребром AD и гранью АВС; 4) площадь грани АВС; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины AD на грань АВС.
Пример 3.Даны координаты вершин пирамиды ABCD: A(2,1,0), B(3,-1,2), C(13,3,10), D(0,1,4). Найти: 1) угол между ребрами AB и AD; 2) уравнение плоскости АВС; 3) угол между ребром AD и гранью АВС; 4) площадь грани АВС; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины AD на грань АВС.
1) Угол между ребрами AB и AD вычисляем по формуле:
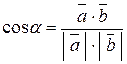 ,
,
где
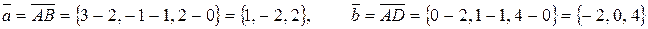
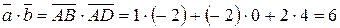 .
.
 ;
;
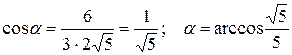 .
.
2) Уравнение плоскости, проходящей через три заданные точки имеет вид:
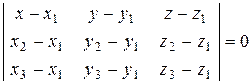 .
.
Подставляя в данное уравнение координаты точек А,В и С, получим:
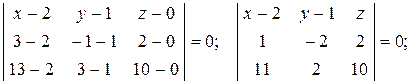
Разложив определитель по элементам первой строки, получим:
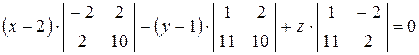 ,
,
отсюда находим искомое уравнение плоскости АВС:
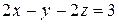 .
.
3) Угол между ребром AD и гранью АВС вычисляем по формуле:
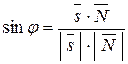 ,
,
где 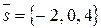 - направляющий вектор ребра AD,
- направляющий вектор ребра AD, 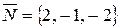 - нормальный вектор грани АВС.
- нормальный вектор грани АВС.
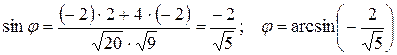 .
.
4) Площадь грани АВС вычисляется по формуле:
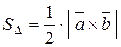 .
.
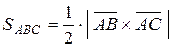 .
.
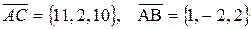 .
.
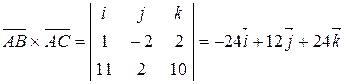 .
.
Окончательно имеем
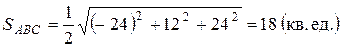
5) Объем пирамиды вычисляем по формуле:
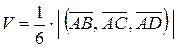 .
.
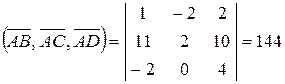 .
.
Объем пирамиды равен 24 (куб. ед.).
6) Уравнение высоты DM, опущенной из вершины D на грань АВС составляет по формуле
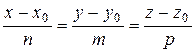 ,
,
где (x0, y0, z0) – координаты точки D, 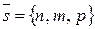 - координаты направляющего вектора прямой DM. Т.к. DM ^ АВС, то в качестве направляющего вектора
- координаты направляющего вектора прямой DM. Т.к. DM ^ АВС, то в качестве направляющего вектора 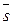 можно взять нормальный вектор
можно взять нормальный вектор 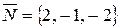 . Уравнение прямой Dm запишется в виде:
. Уравнение прямой Dm запишется в виде:
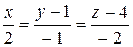 .
.
Дата добавления: 2016-02-16; просмотров: 1585;
