Аналитическая геометрия на плоскости и в пространстве. 1 страница
В этой главе мы изучим фигурах первого и второго порядка на плоскости и в пространстве.
§2.1.Декартова прямоугольная система координат.
2.1.1. Определение. Аффинной (декартовой) системой координатв трехмерном пространстве называется совокупность некоторой точки и произвольного базиса. При этом точка называется началом координат, а прямые, проходящие через начало координат в направлении базисных векторов – осями координат: первая – осью абсцисс (ОХ), вторая – осью ординат (ОY), третья – осью аппликат (OZ).
Замечание.
Аналогично определяются аффинные системы координат на плоскости и прямой.
2.1.2. Определение. Вектор, соединяющий начало координат с некоторой точкой, называется радиусом-вектором этой точки.
2.1.3. Определение. Координатами точки в аффинной системе координат называются координаты ее радиуса-вектора.
2.1.4. Определение. Аффинная система координат, базис которой является ортонормированным, называется прямоугольной декартовой системой координат.
 2.1.5. Параллельный перенос осей.
2.1.5. Параллельный перенос осей.
Пусть новая система координат 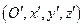 получена из старой
получена из старой 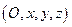 сдвигом на вектор
сдвигом на вектор 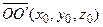 . Тогда
. Тогда 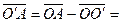
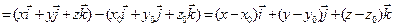 . Базисные орты в обеих системах одинаковы, поэтому координаты вектора
. Базисные орты в обеих системах одинаковы, поэтому координаты вектора 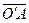 есть координаты точки О’ в новой системе координат:
есть координаты точки О’ в новой системе координат: 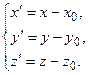
2.1.6. Кривые и поверхности.
Одним из основных вопросов аналитической геометрии является исследование линий на плоскости и поверхностей в пространстве.
2.1.6.1. Определение. Уравнение f(x, y) = 0 называется уравнением линии l на плоскости, если этому уравнению удовлетворяют координаты х, у всех точек М(х, у), лежащих на линии, и не удовлетворяют координаты ни одной точки P(х, у), не лежащей на кривой:
f(x, y) = 0 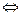 М(х, у)
М(х, у) 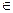 l,
l,
f(x, y) 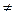 0
0 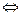 М(х, у)
М(х, у) 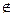 l.
l.
2.1.6.2. Определение. Уравнение F(x, y, z) = 0 называется уравнением поверхности 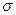 в пространстве, если этому уравнению удовлетворяют координаты х, y, z всех точек М(х, у, z), лежащих на поверхности, и не удовлетворяют координаты ни одной точки P(х, у, z), не лежащей на поверхности:
в пространстве, если этому уравнению удовлетворяют координаты х, y, z всех точек М(х, у, z), лежащих на поверхности, и не удовлетворяют координаты ни одной точки P(х, у, z), не лежащей на поверхности:
F(x, y, z) = 0 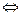 М(х, у, z)
М(х, у, z) 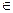
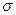 ,
,
F(x, y, z) 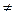 0
0 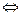 М(х, у, z)
М(х, у, z) 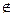
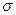 .
.
2.1.7. Две основные задачи аналитической геометрии.
I.Дано некоторое множество точек плоскости (пространства), обладающее некоторым набором свойств. Требуется составить уравнение (или систему уравнений), которое в некоторой системе координат задает это множество точек.
II (обратная). В заданной системе координат некоторое множество точек плоскости (пространства) описывается заданным уравнением (или системой уравнений). Требуется определить вид и основные свойства этого множества и построить его эскиз.
§2.2.Простейшие задачи аналитической геометрии.
2.2.1. Нахождение длины отрезка.
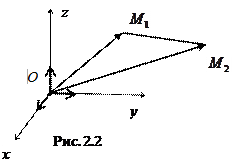
Пусть в заданной декартовой прямоугольной системе координат имеется две точки 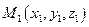 и
и 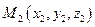 . (Рис. 2.2).
. (Рис. 2.2).
Вектор 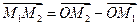 .
.
Следовательно, длина отрезка 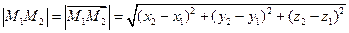 .
.
2.2.2. Деление отрезка в заданном отношении.
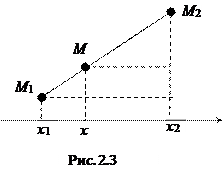 Говорят, что точка М делит отрезок М1М2 в отношении
Говорят, что точка М делит отрезок М1М2 в отношении 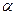 , если
, если 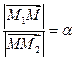 . Найдем координаты точки М. На Рис. 2.3 изображен отрезок и его проекция на ось Ох.
. Найдем координаты точки М. На Рис. 2.3 изображен отрезок и его проекция на ось Ох.
Запишем векторное равенство 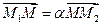 и его проекции на оси координат.
и его проекции на оси координат.
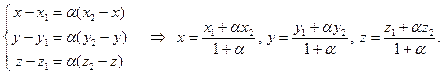
В частном случае 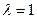 , т.е. когда точка М – середина отрезка, получаем, что координаты середины отрезка равны средним арифметическим координат концов:
, т.е. когда точка М – середина отрезка, получаем, что координаты середины отрезка равны средним арифметическим координат концов:
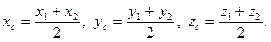
§2.3. Прямая на плоскости.
2.3.1. Общее уравнение прямой.
2.3.1.1. Определение. Ненулевой вектор 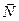 называется нормальным вектором прямой, если он перпендикулярен всякому вектору, лежащему на прямой.
называется нормальным вектором прямой, если он перпендикулярен всякому вектору, лежащему на прямой.
2.3.1.2. Теорема. (Общее уравнение прямой)
 Всякая прямая на плоскости в декартовой прямоугольной системе координат задается уравнением первой степени.
Всякая прямая на плоскости в декартовой прямоугольной системе координат задается уравнением первой степени.
Доказательство:
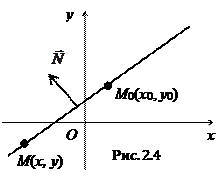
Пусть на плоскости задана точка 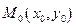 и ненулевой вектор
и ненулевой вектор 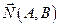 . В аналитической геометрии прямаязадается какгеометрическое место точек
. В аналитической геометрии прямаязадается какгеометрическое место точек 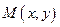 таких, что вектор
таких, что вектор 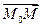 ортогонален вектору
ортогонален вектору 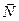 .Таким образом, в векторном виде уравнение прямой записывается так:
.Таким образом, в векторном виде уравнение прямой записывается так:
 .
.
(скалярное произведение ортогональных векторов равно нулю).
Запишем последнее равенство в координатной форме: 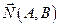 ,
, 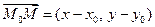 , следовательно, А(х – х0) + В(у – у0) = 0. Преобразуем это уравнение:
, следовательно, А(х – х0) + В(у – у0) = 0. Преобразуем это уравнение:
Ах + Ву + (–Ах0 – Ву0) = 0. Обозначим С = –Ах0 – Ву0, тогда 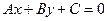 , это уравнение называется общим уравнением прямой.
, это уравнение называется общим уравнением прямой.
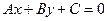 .
.
2.1.3.3. Определение. Уравнение вида
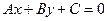 (2.1)
(2.1)
называется общим уравнением прямой.
2.1.3.4. Определение. Уравнение вида
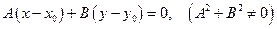 (2.2)
(2.2)
называется уравнением прямой, проходящей через точку 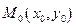 с нормальным вектором
с нормальным вектором 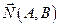 .
.
2.1.3.5. Определение. Линии, которые в декартовой прямоугольной системе координат задаются уравнениями первой степени, называются линиями первого порядка.
2.3.1.6. Теорема. (О линиях первого порядка на плоскости)
Линиями первого порядка на плоскости являются прямые, и только они.
Доказательство:
То, что прямая на плоскости задается уравнением вида 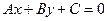 , то есть уравнением первой степени, доказано в теореме 2.1.3.2. Осталось доказать, что всякое уравнение вида
, то есть уравнением первой степени, доказано в теореме 2.1.3.2. Осталось доказать, что всякое уравнение вида 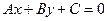 при условии
при условии  задает прямую на плоскости.
задает прямую на плоскости.
Пусть 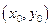 - некоторое решение уравнения (2.1). Тогда при подстановке его в уравнение мы получим тождество:
- некоторое решение уравнения (2.1). Тогда при подстановке его в уравнение мы получим тождество:
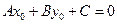 .
.
Вычтем полученное равенство из уравнения (2.1), получим
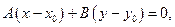
то есть уравнение прямой, проходящей через точку 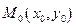 с нормальным вектором
с нормальным вектором 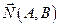
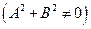 .
.
Таким образом, доказано, что всякое уравнение вида (2.1) при условии  задает прямую и что всякая прямая на плоскости может быть задана уравнением вида (2.1).
задает прямую и что всякая прямая на плоскости может быть задана уравнением вида (2.1).
2.3.1.7. Теорема. (О перпендикулярности прямой и вектора на плоскости)
Для того, чтобы прямая, заданная общим уравнением, была перпендикулярна вектору на плоскости, необходимо и достаточно, чтобы координаты вектора были пропорциональны коэффициентам при переменных общего уравнения прямой, т.е.
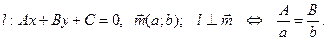
Доказательство:
Очевидно, перпендикулярность прямой и вектора эквивалентно коллинеарности вектора и нормального вектора прямой, следовательно, по критерию коллинеарности (Следствие из теоремы 1.5.6) получаем требуемое.
2.3.1.8. Частные случаи общего уравнения прямой на плоскости.
1. 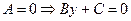 - прямая, параллельная оси абсцисс;
- прямая, параллельная оси абсцисс;
2. 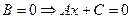 - прямая, параллельная оси ординат;
- прямая, параллельная оси ординат;
3. 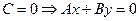 - прямая, проходящая через начало координат;
- прямая, проходящая через начало координат;
4. 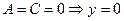 - ось абсцисс;
- ось абсцисс;
5. 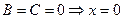 - ось ординат.
- ось ординат.
2.3.2. Уравнение прямой с угловым коэффициентом.
2.3.2.1. Определение. Углом наклона прямой называется любой направленный угол, на который надо повернуть ось Ох, чтобы получить одно из направлений прямой.
Замечание.
Очевидно, все углы наклона прямой отличаются друг от друга на величину 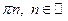 , поэтому их тангенсы равны.
, поэтому их тангенсы равны.
2.3.2.2. Вывод уравнения прямой с угловым коэффициентом.
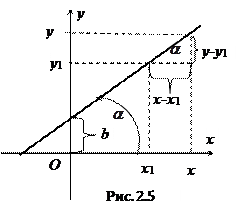
Рассмотрим точку 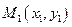 принадлежащую прямой и произвольную точку
принадлежащую прямой и произвольную точку 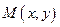 . Очевидно, что если точка
. Очевидно, что если точка 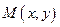 лежит на прямой, то
лежит на прямой, то 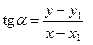 (Рис. 2.5).
(Рис. 2.5).
Обозначим 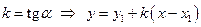 .
.
Полагая 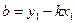 , перепишем уравнение в виде
, перепишем уравнение в виде
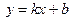 (2.3)
(2.3)
Геометрический смысл коэффициента 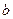 состоит в том, что
состоит в том, что 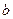 является ординатой точки пересечения прямой с осью Оу. Параметр k, который называют угловым коэффициентом прямой, равен тангенсу угла наклона прямой:
является ординатой точки пересечения прямой с осью Оу. Параметр k, который называют угловым коэффициентом прямой, равен тангенсу угла наклона прямой: 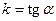 .
.
Уравнение вида (2.3) называется уравнением прямой с угловым коэффициентом.
Замечание.
Так как 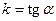 , уравнение с угловым коэффициентом невозможно записать для прямых с
, уравнение с угловым коэффициентом невозможно записать для прямых с 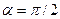 , т.е. для прямых, параллельных оси Оу. Такие прямые имеют уравнение
, т.е. для прямых, параллельных оси Оу. Такие прямые имеют уравнение 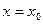 , где
, где 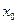 – абсцисса точки пересечения прямой с осью Ох.
– абсцисса точки пересечения прямой с осью Ох.
2.3.3. Связь между общим уравнением прямой и уравнением прямой с угловым коэффициентом.
Запишем уравнение прямой с угловым коэффициентом 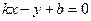 . Обозначая
. Обозначая 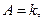
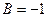 , получим общее уравнение прямой
, получим общее уравнение прямой 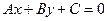 .
.
Обратный переход: если в уравнении 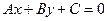 положить
положить 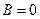 , то прямая не имеет углового коэффициента; если же
, то прямая не имеет углового коэффициента; если же 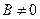 , то
, то 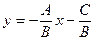 . Обозначая
. Обозначая 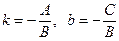 , получим уравнение прямой с угловым коэффициентом
, получим уравнение прямой с угловым коэффициентом 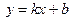 .
.
2.3.4. Уравнение прямой в отрезках.
Рассмотрим прямую, не проходящую через начало координат и заданную своим общим уравнением 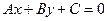
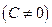 . Представим данное уравнение в виде
. Представим данное уравнение в виде

 .
.
Обозначая 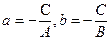 , получим уравнение
, получим уравнение
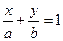 , (2.4)
, (2.4)
которое называется уравнением прямой в отрезках.
Положив в этом уравнении х = 0, получим y = b; положив у = 0, получаем х = а. Таким образом, параметры а и b равны, соответственно, абсциссе и ординате концов отрезков, отсекаемых прямой на осях Ох и Оу. Отметим, что в отрезках может быть записана любая прямая, не проходящая через начало координат.
 2.3.5. Угол между прямыми.
2.3.5. Угол между прямыми.
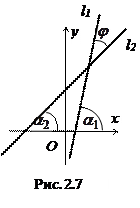
Пусть прямая l1 задана уравнением у = k1х + b1,
прямая l2 задана уравнением у = k2х + b2; тогда 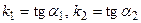 . Обозначим
. Обозначим 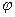 - угол между этими прямыми (Рис. 2.7).
- угол между этими прямыми (Рис. 2.7).
Так как 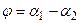 , то
, то
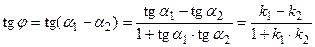 .
.
Таким образом, 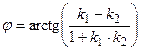 .
.
Если прямые заданы своими общими уравнениями
l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0,
то
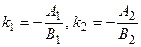 ,
,
и
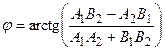 .
.
2.3.5.1. Условия параллельности и перпендикулярности прямых на плоскости.
Из выражений для тангенса угла между прямыми следуют условия параллельности и перпендикулярности прямых:
В случае параллельности прямых l1|| l2 тангенс угла между ними
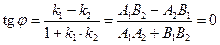 ,
,
следовательно, k1 = k2, или А1В2 = А2В1, или 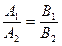 .
.
В случае параллельности прямых 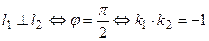 , или А1А2 + В1В2 = 0.
, или А1А2 + В1В2 = 0.
2.3.6. Расстояние от точки до прямой на плоскости.
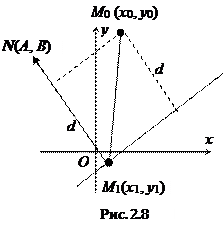 Пусть прямая l задана общим уравнением
Пусть прямая l задана общим уравнением 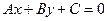 ,
, 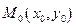 – произвольная точка плоскости. Очевидно, для любой точки М1(x1, y1), лежащей на прямой, расстояние d от точки M0до прямой l равно абсолютной величине проекции вектора
– произвольная точка плоскости. Очевидно, для любой точки М1(x1, y1), лежащей на прямой, расстояние d от точки M0до прямой l равно абсолютной величине проекции вектора 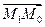 на нормальный вектор
на нормальный вектор 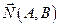 . Пусть точка М1 имеет координаты
. Пусть точка М1 имеет координаты 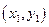 , тогда
, тогда  ,
,
и
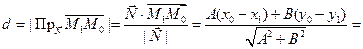
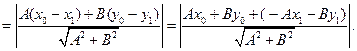
Из принадлежности точки М1 прямой l следует, что 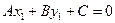 , т.е.
, т.е. 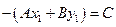 .
.
Следовательно,
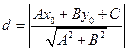 . (2.5)
. (2.5)
Таким образом, чтобы найти расстояние от точки до прямой, достаточно подставить координаты точки в общее уравнение прямой и полученное число разделить на длину нормального вектора.
Лекция 5.
§2.4. Плоскость в пространстве.
2.4.1. Общее уравнение плоскости.
2.4.1.1. Определение. Вектор, перпендикулярный к плоскости, называется ее нормальным вектором.
2.4.1.2. Теорема. (Общее уравнение плоскости).
 В декартовой прямоугольной системе координат плоскость задается уравнением первой степени.
В декартовой прямоугольной системе координат плоскость задается уравнением первой степени.
Доказательство:
Пусть в пространстве задан ненулевой вектор 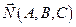 , перпендикулярный плоскости и точка
, перпендикулярный плоскости и точка 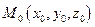 , принадлежащая плоскости. Очевидно, произвольная точка пространства
, принадлежащая плоскости. Очевидно, произвольная точка пространства 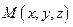 принадлежит плоскости при условии, что вектор
принадлежит плоскости при условии, что вектор 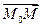 ортогонален вектору
ортогонален вектору 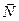 . Таким образом, получаем уравнение
. Таким образом, получаем уравнение
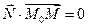 .
.
(скалярное произведение ортогональных векторов равно нулю).
В координатном виде это уравнение имеет вид
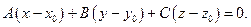
Преобразуем это уравнение: 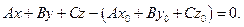 Обозначая
Обозначая 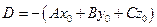 , получим
, получим
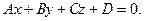
2.4.1.3. Определение. Уравнение вида
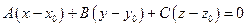 (2.6)
(2.6)
называется уравнением плоскости, проходящей через точку 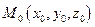 и имеющей нормальный вектор
и имеющей нормальный вектор 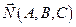 .
.
2.4.1.4. Определение. Уравнение вида
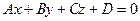 (2.7)
(2.7)
называется общим уравнением плоскости.
2.4.1.5. Связка плоскостей.
Связкой плоскостей называют совокупность плоскостей, проходящих через одну точку. Очевидно, уравнение 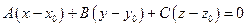 при произвольных (не равных нулю одновременно) коэффициентах А, В, С есть уравнение связки плоскостей, проходящих через точку
при произвольных (не равных нулю одновременно) коэффициентах А, В, С есть уравнение связки плоскостей, проходящих через точку 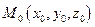 .
.
2.4.1.6. Определение. Поверхность в пространстве, которая в декартовой прямоугольной системе координат задается уравнением первой степени, называется поверхностью первого порядка.
2.4.1.7. Теорема. (О поверхностях первого порядка в пространстве).
Поверхностями первого порядка в пространстве являются плоскости, и только они.
Доказательство:
Поскольку мы уже доказали в теореме 2.4.1.2, что плоскость можно задать уравнением первого порядка, осталось доказать, что уравнение 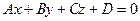 при условии
при условии 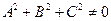 задает плоскость.
задает плоскость.
Пусть 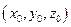 - некоторое решение уравнения (2.7). Тогда при подстановке его в уравнение мы получим тождество:
- некоторое решение уравнения (2.7). Тогда при подстановке его в уравнение мы получим тождество:
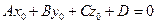 .
.
Вычтем полученное равенство из уравнения (2.7), получим
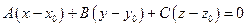 ,
,
то есть уравнение плоскости, проходящей через точку 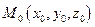 с нормальным вектором
с нормальным вектором 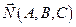
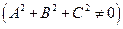 .
.
Таким образом, доказано, что всякое уравнение вида (2.7) при условии 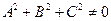 задает плоскость и что всякая плоскость в пространстве может быть задана уравнением вида (2.7).
задает плоскость и что всякая плоскость в пространстве может быть задана уравнением вида (2.7).
2.4.1.8. Частные случаи общего уравнения плоскости.
1. 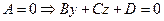 - плоскость, параллельная оси абсцисс;
- плоскость, параллельная оси абсцисс;
2. 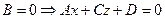 - плоскость, параллельная оси ординат;
- плоскость, параллельная оси ординат;
3. 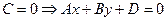 - плоскость, параллельная оси аппликат;
- плоскость, параллельная оси аппликат;
4. 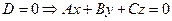 - плоскость, проходящая через начало координат;
- плоскость, проходящая через начало координат;
5. 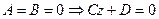 - плоскость, параллельная координатной плоскости XOY;
- плоскость, параллельная координатной плоскости XOY;
6. 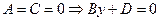 - плоскость, параллельная координатной плоскости XOZ;
- плоскость, параллельная координатной плоскости XOZ;
7. 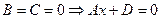 - плоскость, параллельная координатной плоскости YOZ;
- плоскость, параллельная координатной плоскости YOZ;
8. 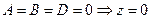 - координатная плоскость XOY;
- координатная плоскость XOY;
9. 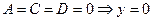 - координатная плоскость XOZ;
- координатная плоскость XOZ;
10. 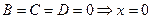 - координатная плоскость YOZ;
- координатная плоскость YOZ;
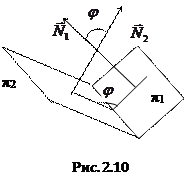 2.4.2. Угол между плоскостями.
2.4.2. Угол между плоскостями.
Пусть даны две плоскости
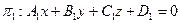 с нормальным вектором
с нормальным вектором 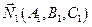
и  с нормальным вектором
с нормальным вектором 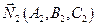 . Очевидно, косинус угла между плоскостями равен косинусу угла между нормальными векторами, поэтому
. Очевидно, косинус угла между плоскостями равен косинусу угла между нормальными векторами, поэтому
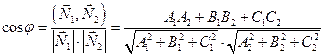 . (2.8)
. (2.8)
Замечание 1.
Если требуется определить острый угол между плоскостями, то
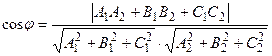 .
.
Замечание 2.
Из формулы угла между плоскостями следуют условия параллельности и перпендикулярности плоскостей.
Дата добавления: 2016-04-14; просмотров: 3473;
