Аналитическая геометрия на плоскости и в пространстве. 4 страница
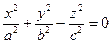 . (2.34)
. (2.34)
Поверхность, определяемая каноническим уравнением вида (2.34), называется конусом второго порядка.
 Изучим поверхность методом сечений.
Изучим поверхность методом сечений.
В плоскости 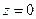 получаем
получаем 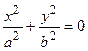 ; единственная точка, удовлетворяющая этому уравнению – точка О(0, 0).
; единственная точка, удовлетворяющая этому уравнению – точка О(0, 0).
В плоскости 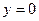 получаем
получаем 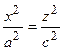 , это уравнение пары прямых
, это уравнение пары прямых 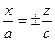 .
.
В плоскости 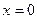 уравнение
уравнение 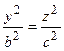 даст пару прямых
даст пару прямых 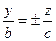 .
.
В плоскостях 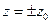 получаем
получаем 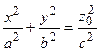 - это уравнение эллипса с полуосями (az0/c) и (bz0/c), линейно расширяющимися с ростом z0.
- это уравнение эллипса с полуосями (az0/c) и (bz0/c), линейно расширяющимися с ростом z0.
В плоскостях 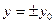 и
и 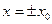 получим гиперболы
получим гиперболы 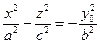 и
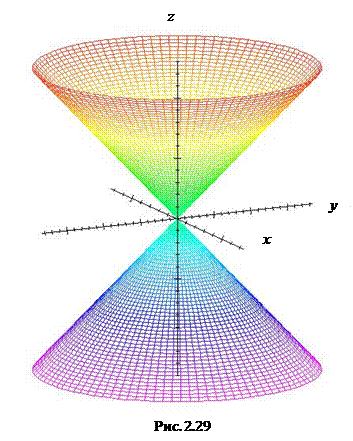
и 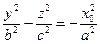 , с мнимой осью Oz. Поверхность изображена на Рис. 2.29.
, с мнимой осью Oz. Поверхность изображена на Рис. 2.29.
2. 8.4.3. Однополостный гиперболоид.
Рассмотрим в плоскости Охz гиперболу с действительной осью Ох 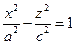 . Вращая кривую вокруг оси Oz, и растягивая получившуюся поверхность вдоль оси Оу , получим
. Вращая кривую вокруг оси Oz, и растягивая получившуюся поверхность вдоль оси Оу , получим 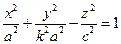 . Обозначая
. Обозначая 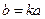 , имеем
, имеем
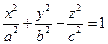 . (2.35)
. (2.35)
Поверхность, определяемая каноническим уравнением вида (2.35), называется однополостным гиперболоидом.
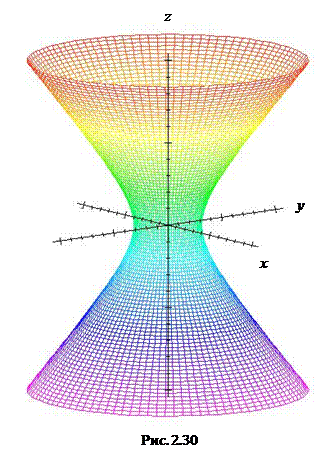
Исследуем однополостный гиперболоид методом сечений. Уравнение пересечения поверхности с плоскостью z = 0 - эллипс 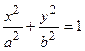 с полуосями a и b. В плоскостях х = 0 и у = 0 получаем гиперболы
с полуосями a и b. В плоскостях х = 0 и у = 0 получаем гиперболы 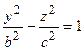 и
и 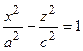 с мнимой осью Oz, в сечениях поверхности плоскостями z =
с мнимой осью Oz, в сечениях поверхности плоскостями z = 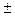 z0 получаем эллипсы
z0 получаем эллипсы 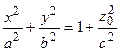 , вершины которых находятся как раз на гиперболах в плоскостях х = 0 и у = 0. В плоскостях
, вершины которых находятся как раз на гиперболах в плоскостях х = 0 и у = 0. В плоскостях 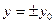 получим гиперболы
получим гиперболы 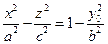 . При условии
. При условии 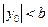 гиперболы будут иметь действительную ось Oх; если
гиперболы будут иметь действительную ось Oх; если 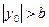 , то мы получим гиперболы с действительной осью Oz; если
, то мы получим гиперболы с действительной осью Oz; если 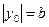 , то в сечении получим пары пересекающихся прямых. Аналогично рассматривается сечение плоскостями
, то в сечении получим пары пересекающихся прямых. Аналогично рассматривается сечение плоскостями 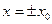 . Получим уравнение
. Получим уравнение 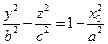 , то есть гиперболы с действительной осью Oz при
, то есть гиперболы с действительной осью Oz при 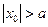 , с мнимой осью Oz при
, с мнимой осью Oz при 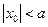 , и пары пересекающихся прямых при
, и пары пересекающихся прямых при 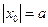 . Поверхность изображена на Рис. 2.30.
. Поверхность изображена на Рис. 2.30.
2. 8.4.4. Двуполостный гиперболоид.
Рассмотрим в плоскости Охz гиперболу с действительной осью Оz 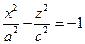 . Как и в случае предыдущих поверхностей, вращаем кривую вокруг оси Oz и растягиваем получившуюся поверхность вдоль оси Оу , получим
. Как и в случае предыдущих поверхностей, вращаем кривую вокруг оси Oz и растягиваем получившуюся поверхность вдоль оси Оу , получим
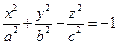 , (2.36)
, (2.36)
где 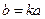 .
.
Поверхность, определяемая каноническим уравнением вида (2.36), называется двуполостным гиперболоидом.
 Рассмотрим сечения двуполостного гиперболоида координатными плоскостями, а также параллельными им плоскостями.
Рассмотрим сечения двуполостного гиперболоида координатными плоскостями, а также параллельными им плоскостями.
При сечении плоскостями 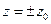 получим
получим 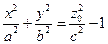 , откуда при
, откуда при 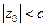 (включая плоскость
(включая плоскость 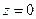 ) получим мнимый эллипс; при
) получим мнимый эллипс; при 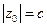 получим две точки с координатами
получим две точки с координатами 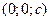 и
и 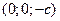 ; при
; при 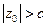 получим уравнение эллипса. В плоскостях
получим уравнение эллипса. В плоскостях 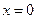 и
и 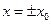 получаем гиперболы с действительной осью Оz
получаем гиперболы с действительной осью Оz 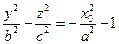 . Аналогично при сечении плоскостями
. Аналогично при сечении плоскостями 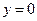 и параллельных им плоскостях
и параллельных им плоскостях 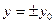 получаем гиперболы с действительной осью Оz
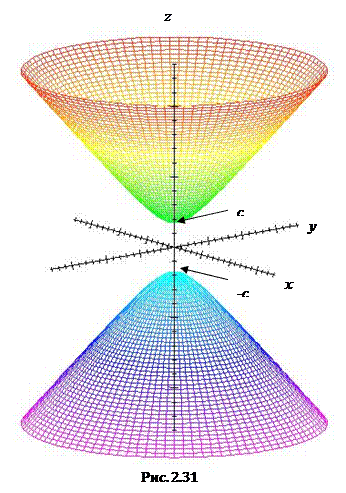
получаем гиперболы с действительной осью Оz 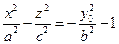 . Иллюстрация двуполостного гиперболоида приведена на Рис. 2.31.
. Иллюстрация двуполостного гиперболоида приведена на Рис. 2.31.
2.8.4.5. Эллиптический параболоид.
 Рассмотрим в плоскости Охz параболу с уравнением
Рассмотрим в плоскости Охz параболу с уравнением 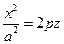 . Вращая ее вокруг оси Oz и растягивая получившуюся поверхность вдоль оси Оу , получим
. Вращая ее вокруг оси Oz и растягивая получившуюся поверхность вдоль оси Оу , получим
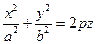 , (2.37)
, (2.37)
где 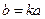 .
.
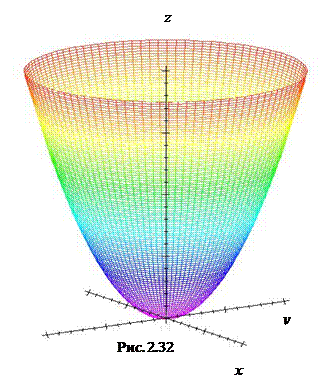
Поверхность, имеющая каноническое уравнение вида (2.37), называется эллиптическим параболоидом.
Сечения плоскостями 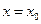 и
и 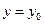 дают параболы
дают параболы 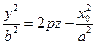 и
и 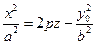 . В сечении z = z0
. В сечении z = z0 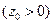 получим эллипс
получим эллипс 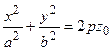 , при
, при 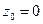 эллипс вырождается в точку, а при
эллипс вырождается в точку, а при 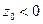 имеем мнимый эллипс. Поверхность изображена на Рис. 2.32.
имеем мнимый эллипс. Поверхность изображена на Рис. 2.32.
2.8.4.6. Гиперболический параболоид.
Данная фигура не может быть получена вращением какой-либо кривой второго порядка. Каноническое уравнение этой поверхности
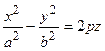 . (2.38)
. (2.38)
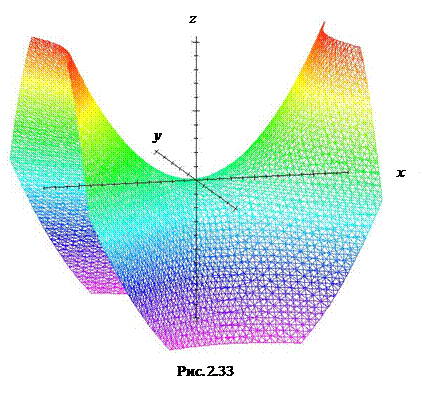 Исследуем поверхность методом сечений. В плоскости у = 0 получим параболу
Исследуем поверхность методом сечений. В плоскости у = 0 получим параболу 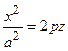 , ветви которой направлены вверх вдоль оси Oz; в плоскости х = 0 - параболу
, ветви которой направлены вверх вдоль оси Oz; в плоскости х = 0 - параболу 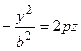 , ветви которой направлены вниз вдоль оси Oz; в плоскости
, ветви которой направлены вниз вдоль оси Oz; в плоскости 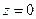 получим две пересекающиеся прямые
получим две пересекающиеся прямые 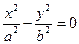 . Рассмотрим сечения плоскостями, параллельными координатным плоскостям. В сечении плоскостью
. Рассмотрим сечения плоскостями, параллельными координатным плоскостям. В сечении плоскостью 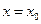 будут параболы
будут параболы 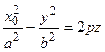 , которые получаются перемещением вершин парабол
, которые получаются перемещением вершин парабол 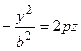 в точку, лежащую на параболе
в точку, лежащую на параболе 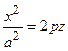 при
при 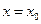 . Аналогично при сечении плоскостью
. Аналогично при сечении плоскостью 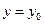 имеем параболы
имеем параболы 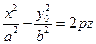 , которые получаются перемещением вершин парабол
, которые получаются перемещением вершин парабол 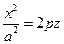 в точку, лежащую на параболе
в точку, лежащую на параболе 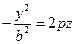 при
при 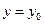 . При сечении плоскостью
. При сечении плоскостью 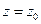 получим
получим 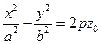 , то есть при
, то есть при 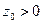 сечениями будут гиперболы с действительной осью Ох , а при
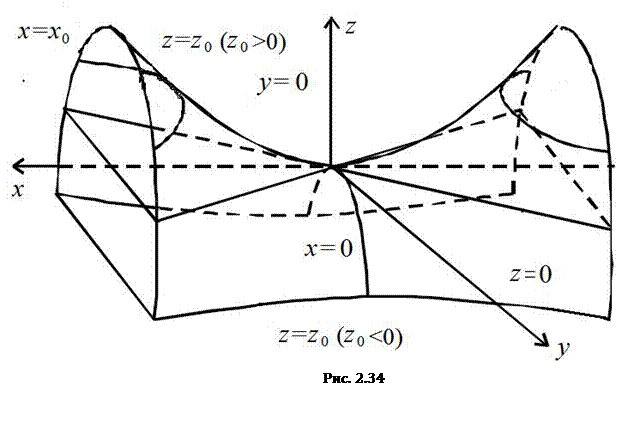
сечениями будут гиперболы с действительной осью Ох , а при 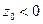 − гиперболы с действительной осью Оу. Поверхность изображена на Рис. 2.33. Дополнительно на Рис. 2.34 показаны сечения гиперболического параболоида координатными плоскостями и параллельными им плоскостями.
− гиперболы с действительной осью Оу. Поверхность изображена на Рис. 2.33. Дополнительно на Рис. 2.34 показаны сечения гиперболического параболоида координатными плоскостями и параллельными им плоскостями.
 Таким образом, нами рассмотрены следующие основные поверхности второго порядка:
Таким образом, нами рассмотрены следующие основные поверхности второго порядка:
- Эллиптический цилиндр
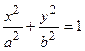 ;
;
- Гиперболический цилиндр
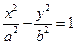 ;
;
- Параболический цилиндр
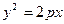 ;
;
- Эллипсоид
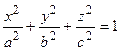 ;
;
- Конус второго порядка
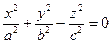 ;
;
- Однополостный гиперболоид
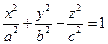 ;
;
- Двуполостный гиперболоид
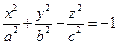 ;
;
- Эллиптический параболоид
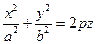 ;
;
9.Гиперболический параболоид 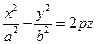 .
.
Дата добавления: 2016-04-14; просмотров: 1777;
