Аналитическая геометрия на плоскости и в пространстве. 3 страница
3. Если провести через фокусы ось Оу и провести аналогичные рассуждения, то фокусами являются точки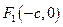 
и 
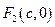, точка 
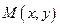удовлетворяет уравнению
,
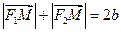откуда получим каноническое уравнение эллипса
,
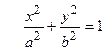где малая полуось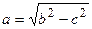 
. В этом случае эксцентриситет 
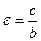, большая полуось расположена на оси Оу (Рис. 2.19).
2.7.5. Гипербола.
2.7.5.1. Определение. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух данных точек, называемых фокусами, является постоянной величиной.
2.7.5.2. Каноническое уравнение гиперболы.
Вывод канонического уравнения гиперболы аналогичен соответствующему выводу для эллипса.
Введем на плоскости прямоугольную систему координат. Направим ось Ох вдоль линии, соединяющей фокусы F1 и F2, с серединой отрезка F1F2, а ось Оу – перпендикулярно через середину отрезка F1F2.
Пусть расстояние между фокусами равно 2с, а модуль разности расстояний от фокусов до произвольной точки равен 2а (a < c).
Тогда фокусы имеют координаты F1(-c, 0) и F2(c, 0), и, если 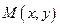– текущая точка эллипса, то расстояния от этой точки до фокусов равны длинам фокальных радиусов F1M и F2M:
,
.
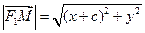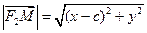Тогда из определения гиперболы
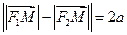, то есть 
.
Избавимся от иррациональности в полученном уравнении
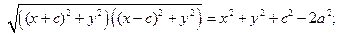
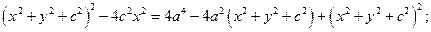
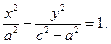
Обозначая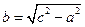 
, получим уравнение
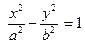, (2.26)
которое и будет каноническим уравнением гиперболы.
2.7.5.3. Свойства гиперболы.
1. Из уравнение (2.26) следует, что 
; следовательно, гипербола имеет две ветви.
2. Поскольку в уравнение входят только четные степени х, у, оси Oх и Оу являются осями симметрии гиперболы, а точка О(0, 0) является центром симметрии.
3. В первом квадранте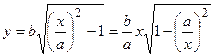 
. Если x = а, то у = 0; у возрастает вместе с х. При больших х функция 
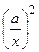- бесконечно малая, и ей можно пренебречь, т.е. прямая 
является наклонной асимптотой при 
(строго это можно показать методами математического анализа). Вследствие симметрии прямая является асимптотой гиперболы и при 
, по той же причине прямая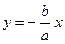 
также является двусторонней асимптотой.
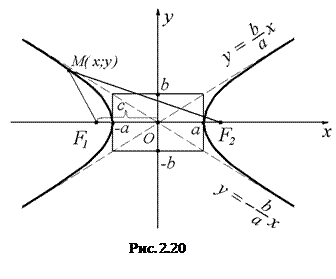Кривая, имеющая эти свойства, изображена на Рис. 2.20.
Параметр а называют действительной полуосью гиперболы, параметр b –мнимой полуосью. Ось, имеющая с гиперболой две общие точки (на Рис. 2.20 ось Ох) называется действительной осью гиперболы. Ось, не имеющая общих точек с гиперболой, называется мнимой осью гиперболы. Число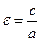 
называется эксцентриситетом гиперболы. Так как a < c, то 
.
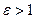Замечание.
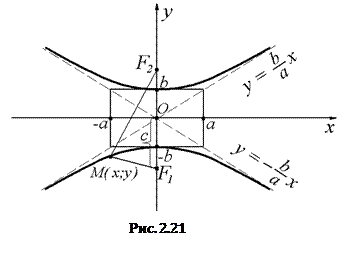Если расположить фокусы гиперболы на оси Оу: F1(0, -c), F2(0, c) (Рис. 2.21), произвольная точка 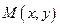гиперболы будет удовлетворять уравнению
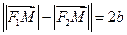, b < c,
параметр а вводится соотношением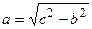 
, эксцентриситет гиперболы 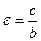, действительная полуось гиперболы будет равна b, мнимая – а, каноническое уравнение примет вид
.
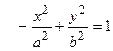В этом случае действительной осью гиперболы будет ось Оу, а мнимой – ось Ох.
2.7.6. Парабола.
2.7.6.1. Определение. Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки, называемой фокусом параболы и заданной прямой этой плоскости, называемой директрисой.
2.7.6.2. Каноническое уравнение параболы.
Пусть на плоскости задана точка F (фокус параболы) и прямая (директриса параболы). Расстояние между фокусом и директрисой равно р (параметр параболы). Проведем ось Ох через фокус перпендикулярно директрисе в направлении от директрисы к фокусу, а ось Оу – параллельно директрисе через середину отрезка, соединяющего фокус с точкой пересечения директрисы и оси абсцисс (Рис 2.22).
Пусть произвольная точка 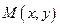принадлежит параболе. 
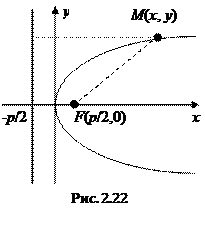Тогда из определения параболы в координатной форме получим:
.
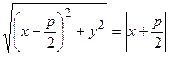После возведения в квадрат и очевидных преобразований имеем
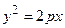. (2.27)
Это уравнение называется каноническим уравнением параболы.
2.7.6.3. Свойства параболы.
1. Из уравнение (2.27) видно, что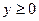 
; следовательно, график параболы расположен в правой полуплоскости.
2. Поскольку в уравнение входит только четная степень у, ось Oх является осью симметрии параболы.
Замечание.
Если направить ось абсцисс через фокус перпендикулярно директрисе в направлении от фокуса к директрисе, то уравнение параболы будет иметь вид
.
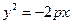
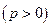Если же расположить ось ординат параллельно директрисе, то мы получим соответственно
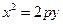и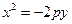 
в зависимости от направления оси ординат (от директрисы к фокусу или от фокуса к директрисе, соответственно). Вышеописанные случаи расположения параболы на плоскости и их соответствующие канонические уравнения приведены на Рис. 2.23.
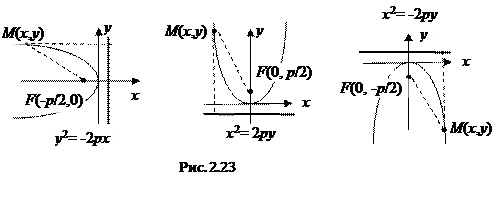
2.7.7. Смещенные кривые второго порядка.
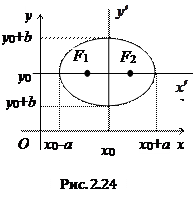Рассмотрим, как преобразуются уравнения эллипса, гиперболы, параболы, если их центры не совпадают с началом системы координат, но оси остаются параллельными координатным осям. Рассмотрим, например, эллипс с центром в точке с координатами (х0, у0), изображенный на Рис. 2.24. В координатах
полученных в результате параллельного переноса, уравнение эллипса имеет канонический вид
.
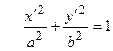Таким образом, в исходных координатах уравнение смещенного эллипса будет
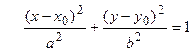. (2.28)
Аналогично для смещенных гипербол уравнения будут иметь вид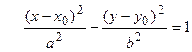 
или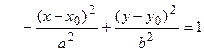 
; (2.29)
для смещенных парабол:
, 
,
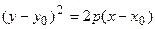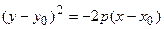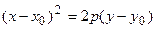или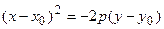 
. (2.30)
2.7.8. Общее уравнение кривой второго порядка.
2.7.8.1. Определение. Уравнение вида
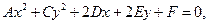
(2.31)
называется общим уравнением кривой второго порядка.
Рассмотрим возможные знаки коэффициентов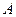 
и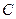 
.
2.7.8.2. Определение. Уравнение вида (2.31) называется уравнением эллиптического типа, если коэффициенты при старших степенях имеют один знак, т.е.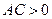 
.
2.7.8.3. Исследование уравнения эллиптического типа.
Выделим в уравнении (2.31) полные квадраты. Предположим, что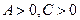 
(в противном случае уравнение можно умножить на -1).
Получим:
,
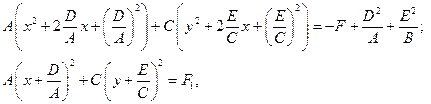где 
.
Выполним параллельный перенос системы координат:
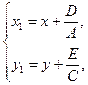
тогда уравнение примет вид
.
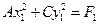Возможны три случая:
1. если 
, то уравнение
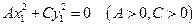
имеет единственное решение, то есть эллипс вырождается в точку (0,0);
2. если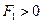 
, получим
,
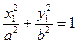где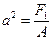 
, 
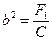, то есть уравнение эллипса;
3. если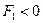 
, то уравнение может быть преобразовано к виду
,
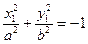где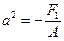 
, 
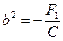. Очевидно, полученное уравнение не имеет действительных решений. В этой связи обычно говорят, что уравнение характеризует мнимый эллипс.
2.7.8.4. Определение. Уравнение вида (2.31) называется уравнением гиперболического типа, если коэффициенты при старших степенях имеют разные знаки, т.е.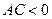 
.
2.7.8.5. Исследование уравнения гиперболического типа.
Предположим без ограничения общности, что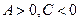 
. Как и при исследовании уравнения эллиптического типа, выделим полные квадраты. Получим уравнение
, ,
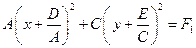причем снова имеем три возможных случая:
1. если 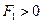, получаем каноническое уравнение гиперболы
,
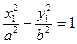с действительной полуосью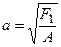 
, мнимой полуосью 
.
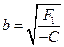2. Если , получаем уравнение 
. Раскладывая левую часть уравнения на множители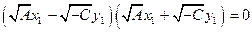 
, получим уравнение пары пересекающихся прямых 
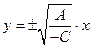. Можно считать, что в этом случае гипербола вырождается в асимптоты.
3. Если 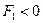, то уравнение преобразуется к виду 
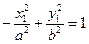гиперболы с мнимой полуосью 
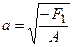, действительной полуосью 
.
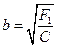2.7.8.6. Определение. Уравнение вида (2.31) называется уравнением параболического типа, если один из коэффициентов при старших степенях равен нулю, т.е.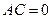 
.
2.7.8.7. Исследование уравнения параболического типа.
Будем считать для определенности, что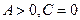 
. Уравнение 
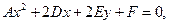представим в виде
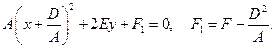
Возможны следующие случаи:
1. Е = 0. Тогда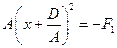 
.
Если правая часть этого уравнения положительна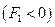 
, то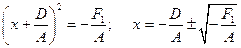 
, т.е. уравнение определяет пару параллельных прямых. Если , получаем пару совпавших прямых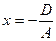 
. Если правая часть отрицательна 
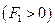, имеем пара мнимых прямых.
2. 
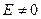. Приведем уравнение к виду
.
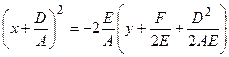Если обозначить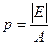 
, и произвести параллельный перенос осей координат
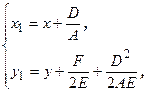
получим каноническое уравнение параболы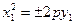 
в зависимости от знака коэффициента 
.
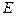Лекция 8.
§2.8.Поверхности второго порядка.
2.8.1. Определение.Поверхностью второго порядка называется множество точек пространства, которое в декартовой системе координат определяется уравнением
(2.32)
2.8.2. Цилиндрические поверхности.
2.8.2.1. Определение. Пусть в пространстве задана прямая l и кривая L, не являющаяся прямой, параллельной l. Цилиндрической поверхностью называется поверхность, образованная множеством прямых, параллельных l и проходящих через точки L (Рис. 2.25) Кривая L называется направляющей цилиндрической поверхности; прямые, параллельные l, из которых состоит поверхность, называются образующими цилиндрической поверхности.
2.8.2.2. Теорема. (Уравнение цилиндрической поверхности)
Всякое уравнение вида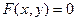 
определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси 
.
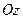Доказательство:
Введем в пространстве декартову систему координат так, чтобы ось 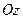была параллельна прямой l, и, как следствие, образующим поверхности (Рис. 2.26). Будем считать, что пересечение поверхности с плоскостью 
определяет кривую L, имеющую уравнение 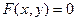. Если этому уравнению удовлетворяет точка 
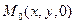, принадлежащая кривой L, то ему удовлетворяет и любая точка 
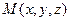при любом z (так как координата z в уравнении в явном виде отсутствует), т.е. любая точка образующей. Таким образом, уравнение 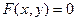определяет всю цилиндрическую поверхность.
Замечание.
Аналогично изложенному можно доказать, что цилиндрическая поверхность с образующими, параллельными оси Oу, определяется уравнением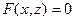 
, а поверхность с образующими, параллельными оси Oх, определяется уравнением 
.
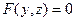2.8.2.3. Цилиндрические поверхности второго порядка.
Каноническим уравнениям кривых второго порядка в пространстве можно поставить в соответствие следующие цилиндрические поверхности:
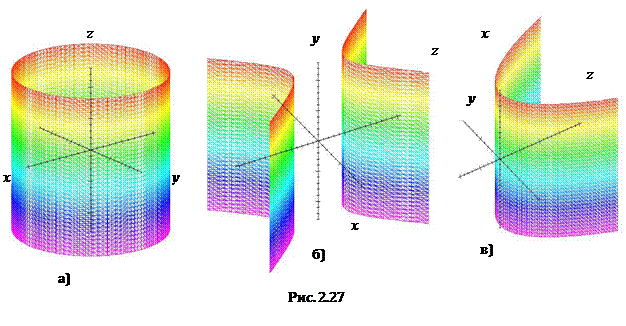
а) Эллиптический цилиндр. В случае образующих, параллельных оси 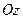(Рис. 2.27а), получим уравнение:
.
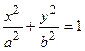б) Гиперболический цилиндр.Приведем уравнение этой поверхности в случае, когда образующие параллельны оси Oу, а направляющей является гипербола с действительной осью Оz (Рис. 2.27б):
.
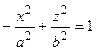в) Параболический цилиндр. Рассмотрим случай, когда направляющей цилиндрической поверхности является парабола в плоскости Oyz, а образующие параллельны оси Ox (Рис. 2.27в). Уравнение поверхности имеет вид
.
2.8.3. Поверхности вращения.
2.8.3.1. Определение. Пусть в плоскости задана прямая l и кривая L. Поверхность, составленная окружностями, которые образуются при вращении всех точек кривой L вокруг l,называется поверхностью вращения,полученной вращением кривой L вокруг прямой l.
2.8.3.2. Теорема. (Уравнение поверхности вращения)
Уравнение поверхности вращения кривой L, заданной в плоскости Оxz своим уравнением 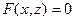, вокруг оси Oz имеет вид
.
Доказательство:
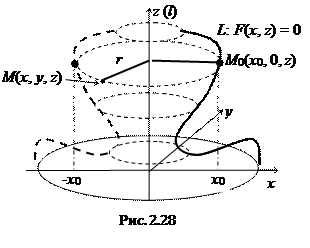
Пусть кривая L , заданная в плоскости Оxz, определяется некоторым уравнением .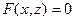
Рассмотрим точку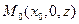 
, принадлежащую кривой L (Рис. 2.28). Радиус r окружности, по которой движется точка 
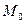, равен расстоянию от этой точки до оси Oz, т.е. 
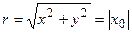. Следовательно, так как x0 удовлетворяет уравнению F(x0, z) = 0, то любая точка окружности удовлетворяет уравнению 
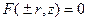, где знак выбирается в соответствии со знаком x.
Таким образом, уравнение поверхности вращения будет , где знак «+» берется, если поверхность порождается точками с положительной абсциссой; если поверхность порождается точками с отрицательной абсциссой, берется знак «-». Теорема доказана.
Пример.
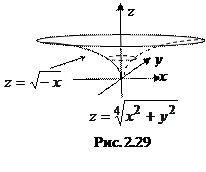Рассмотрим поверхность, полученную в результате вращения вокруг оси Oz кривой 
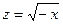, определенной при 
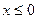(Рис. 2.29). В соответствии с доказанной теоремой в уравнении кривой мы должны заменить х на 
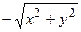, в результате получим 
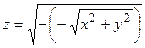, то есть 
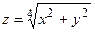. Естественно, это поверхность уже не будет поверхностью второго порядка.
Замечание.
Аналогично можно рассмотреть случаи вращения кривых, заданных в других координатных плоскостей вокруг иных осей вращения. Например, уравнение поверхности вращения кривой L, заданной в плоскости Оxy своим уравнением 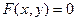, вокруг оси Oy имеет вид
.
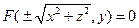2.8.4. Канонические уравнения и изображения поверхностей второго порядка.
При изучении нижеследующих поверхностей второго порядка мы будем пользоваться приемом, который называется методом сечений. Он заключается в том, что для изображения поверхности мы рисуем кривые, которые получаются при пересечении поверхности с координатными плоскостями, а также с плоскостями, параллельными координатным и представляем, как расположена поверхность между этими сечениями.
2.8.4.1. Эллипсоид.
Рассмотрим эллипс в плоскости Охz с уравнением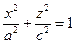 
. Будем вращать эллипс вокруг оси Oz, получим поверхность вращения с уравнением 
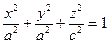. Растягивая вдоль оси Оу , получим 
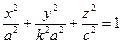. Обозначая 
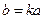, окончательно получим
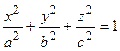. (2.33)
Поверхность, определяемая каноническим уравнением вида (2.33), называется эллипсоидом.
Исследуем эту поверхность методом сечений.
В координатной плоскости z = 0 (т.е. Оху) след этой поверхности есть эллипс ;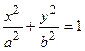
в плоскости у = 0 получаем эллипс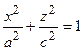 
; в плоскости х = 0 - эллипс 
.
При сечении плоскостями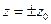 
(т.е. плоскостью, параллельной координатной плоскости Оху), получим 
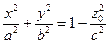. При 
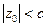получим эллипс, с ростом абсолютной величины 
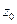при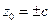 
эллипс вырождается в точку, а при дальнейшем росте абсолютной величины 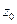при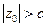 
получим мнимый эллипс.
Аналогичная ситуация будет при сечении плоскостями, параллельными координатным плоскостям Охz и Оуz.
Поверхность изображена на Рис.2.28. Отметим, что координатные оси являются осями симметрии эллипсоида.
2.8.4.2. Конус второго порядка.
Рассмотрим в плоскости Охz две пересекающие прямые (случай вырожденной гиперболы), заданные уравнением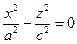 
. Вращая кривую вокруг оси Oz, и растягивая получившуюся поверхность вдоль оси Оу , получим 
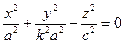. Обозначая 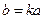, окончательно получим
Дата добавления: 2016-04-14; просмотров: 1745;