Аналитическая геометрия на плоскости и в пространстве. 2 страница

1. Если плоскости параллельны 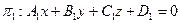и , то их нормальные векторы коллинеарны, то есть их координаты пропорциональны:

.

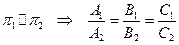Если же выполняются равенства 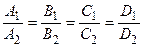, то уравнения 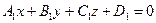и 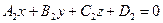определяют одну и ту же плоскость.

2. Если плоскости перпендикулярны, то их нормальные векторы ортогональны, то есть их скалярное произведение равно нулю

.

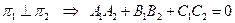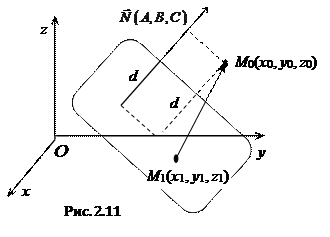2.4.3 Расстояние от точки до плоскости.

Пусть плоскость π задана уравнением 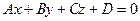, 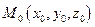– произвольная точка пространства. Для любой точки 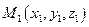, лежащей на плоскости, расстояние d от точки 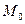до плоскости π равно абсолютной величине проекции вектора 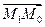на нормальный вектор .

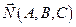Вектор 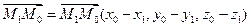, следовательно

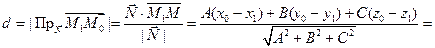
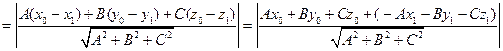
Так как из принадлежности точки 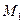плоскости π следует, что 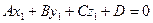, т.е. 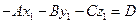, то

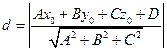. (2.9)

2.4.4. Уравнение плоскости, проходящей через три заданные точки.

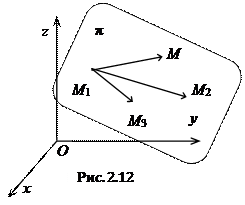Пусть даны три точк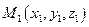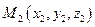и , и 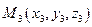, не лежащие на одной прямой (т.е. векторы 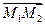и 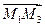не коллинеарны). Введем в задачу точку 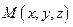– текущую точку плоскости. Векторы 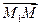, 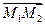и 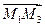лежат в одной плоскости, т.е. компланарны, следовательно, их смешанное произведение равно нулю: 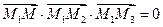, или, в координатной форме,

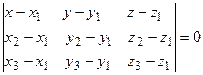. (2.10)

Уравнение вида (2.10) называется уравнением плоскости, проходящей через три данные точки.

2.4.5. Уравнение плоскости в отрезках.

Рассмотрим плоскость, не проходящую через начало координат и заданную своим общим уравнением 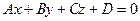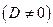. Представим данное уравнение в виде

.

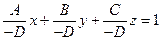Обозначая 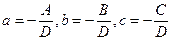, получим уравнение

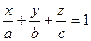, (2.11)

которое называется уравнением плоскости в отрезках.К виду в отрезках может быть приведено уравнение всякой плоскости, не проходящей через начало координат.

Замечание.

Отметим, что точки с координатами (a;0;0), (0;b;0) и (0;0;c) являются точками

пересечения плоскости с осями координат.

Лекция 6.

§2.5.Прямая в пространстве.

2.5.1. Общие уравнения прямой.

В пространстве прямая определяется пересечением двух плоскостей: .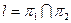

2.5.1.1. Определение. Система уравнений

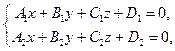(2.12)

называется общими уравнениями прямой в пространстве.

2.5.1.2. Теорема.

Система уравнений вида (2.12) задает прямую в пространстве тогда и только тогда, когда коэффициенты 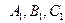не пропорциональны коэффициентам .

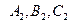Доказательство очевидно, так как пропорциональность коэффициентов эквивалентна параллельности плоскостей.

2.5.1.3. Определение. Пучком плоскостей называется совокупность всех плоскостей, проходящих через одну и ту же прямую.

Замечание.

Если прямая определяется уравнениями двух плоскостей, принадлежащих пучку плоскосте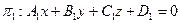й, и , то уравнение пучка плоскостей можно представить в виде линейной комбинации данных уравнений, то есть 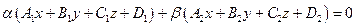. Полученное уравнение называется уравнением пучка плоскостей.

2.5.2. Определение. Ненулевой вектор 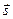, параллельный прямой 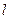, называется направляющим вектором прямой .

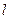2.5.3. Векторное, параметрические и канонические уравнения прямой.

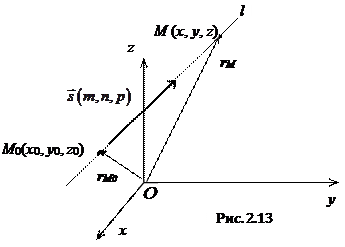Пусть в пространстве задан ненулевой вектор 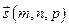и точка 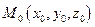. Проведем прямую через точку 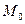в направлении вектора 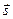. Очевидно, произвольная точка 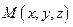принадлежит прямой при условии, что вектор 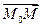коллинеарен вектору .

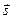Так как вектор 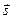является ненулевым, условие коллинеарности векторов 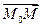и и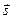меет вид 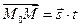. Если 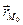– радиус-вектор точки 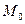, 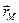– радиус-вектор точки 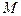, то для любой точки М прямой выполняется 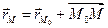, или

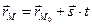. (2.13)

Это уравнение называется векторным уравнением прямой в пространстве.

Запишем векторное уравнение (2.13) в координатной форме. Так как 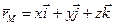, , 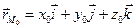получим

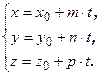(2.14)

Эти уравнения называется параметрическими уравнением прямой в пространстве.Исключим из этих уравнений параметр t: 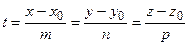. Уравнения

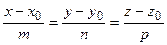(2.15)

называется каноническими уравнениями прямой в пространстве.

2.5.4. Связь общих уравнений прямой с параметрическими.

Для того, чтобы записать параметрические уравнения прямой, заданной своими общими уравнениями

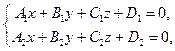
необходимо:

1. Найти направляющий вектор прямой;

2. Найти точку, принадлежащую прямой.

Направляющий вектор 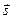находится как векторное произведение векторов нормали плоскостей, задающих прямую вектором 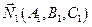и :

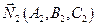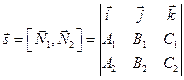
Для того, чтобы найти координаты какой-либо точки, принадлежащей прямой, требуется решить систему из двух уравнений с тремя неизвестными. Так как векторы 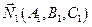и 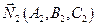неколлинеарны (их координаты непропорциональны), то эта система имеет решение.

Пример.

Пусть прямая задана своими общими уравнениями:

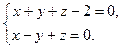
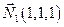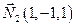Найдем координаты нормальных векторов пересекающихся плоскостей, задающих прямую и . Следовательно, направляющий вектор прямой

.

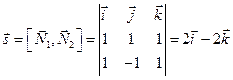Итак, 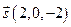. Найдем теперь какое-либо решение исходной системы уравнений. Складываем и вычитаем уравнения, получим:

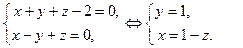
Полагая 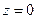, получим одну из точек, принадлежащих прямой .

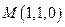Таким образом, имеем направляющий вектор 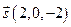и точку 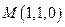, следовательно, параметрические уравнения прямой имеют вид

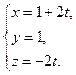
Замечание.

Заметим, что уравнение одной и той же прямой можно записать разными способами. Это определяется произвольностью выбора точки, принадлежащей прямой, а также произвольностью выбора направляющего вектора. Так, например, в предыдущем примере мы могли положить 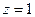и получить точку 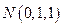, а в качестве направляющего взять вектор 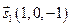, коллинеарный с найденным вектором 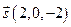. Тогда параметрические уравнения той же прямой, очевидно, принимают вид

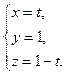
2.5.5. Уравнение прямой, проходящей через две заданные точки.

Пусть заданы две точки 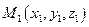, 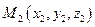и требуется найти уравнение прямой, проходящей через эти две точки. Очевидно, можно взять вектор 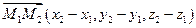в качестве направляющего вектора прямой, а в качестве точки, принадлежащей прямой, можно взять любую из точек М₁ или М₂. Следовательно, канонические уравнения прямой имеют вид:

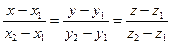(2.16)

2.5.6. Угол между прямыми.

Рассмотрим две прямые, заданные своими каноническими уравнениям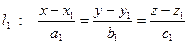и

и .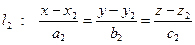

Очевидно, угол между прямыми будет равен углу между их направляющими векторам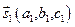и и :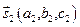

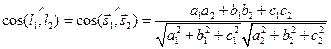. (2.17)

В частности,

если прямые параллельны, то координаты их направляющих векторов пропорциональны

;

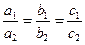если прямые перпендикулярны, то их направляющие векторы ортогональны

.

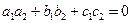§2.6.Взаимное расположение прямых и плоскостей в пространстве.

2.6.1. Взаимное расположение прямой, заданной общими уравнениями, и плоскости.

В пространстве прямая может

а) пересекать плоскость;

б) быть параллельной плоскости;

в) лежать в плоскости.

Пусть плоскость задана общим уравнением

,

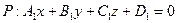а прямая 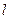задана общими уравнениями

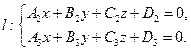
Тогда взаимное расположение прямой и плоскостью определяется системой трех линейных уравнений относительно трех неизвестных:

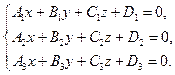(2.18)

Если система уравнений (2.18) имеет единственное решение, то прямая и плоскость пересекаются; если у системы нет решений, то прямая параллельная плоскости; и, наконец, если у системы бесконечное множество решений, то прямая лежит в плоскости.

2.6.2. Взаимное расположение прямой, заданной параметрическими уравнениями, и плоскости.

Пусть плоскость 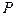задана общим уравнением

,

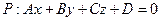а прямая 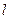задана параметрическими уравнениями

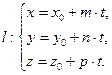
Подставим параметрические уравнения в уравнение плоскости. Получим линейное уравнение относительно параметра t

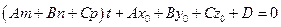. (2.19)

Если выполняется условие 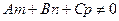, то уравнение (2.19) разрешимо относительно параметра t

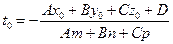, (2.20)

и координаты точки пересечения прямой и плоскости имеют вид

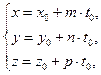
где 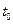определяется из (2.20).

Если 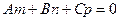, при этом 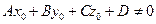, то уравнение (2.19) не разрешимо относительно параметра t, то есть прямая не пересекает плоскость. Таким образом, условие параллельности прямой и плоскости имеет вид

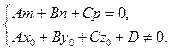
Если же оба коэффициента уравнения (2.19) равны нулю, то оно справедливо для любого значения параметра, то есть имеет бесконечное множество решений. Следовательно, прямая лежит в плоскости при условии

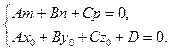
2.6.3. Угол между прямой и плоскостью.

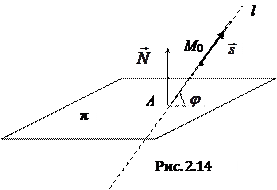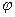Угол между прямой и плоскостью (т.е. угол между прямой и ее проекцией на плоскость) связан с углом 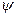между прямой и нормалью к плоскости соотношением 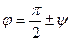, поэтому

.

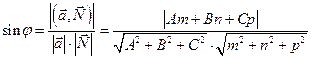В частности, если векторы 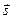и 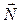коллинеарны, то есть

,

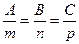то прямая перпендикулярна плоскости.

2.6.4. Взаимное расположение двух прямых.

Две прямые в пространстве могут

а) быть компланарными, в том числе пересекаться, быть параллельными или совпадать;

б) не быть компланарными, то есть скрещиваться.

Пусть две прямые заданы своими каноническими уравнениями

, .

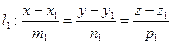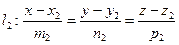Прямые компланарны тогда, и только тогда, когда компланарны векторы 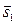, 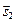и 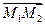. Таким образом, условие компланарности прямых l₁ и l₂ имеет вид

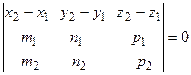. (2.21)

Если при этом векторы 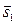, 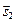коллинеарны, т.е. 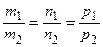, то прямые параллельны. Если, дополнительно, вектор 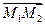коллинеарен направляющим векторам, то прямые совпадают.

Если условие компланарности выполняется, но направляющие векторы неколлинеарны, то прямые пересекаются. Чтобы найти точку пересечения, надо решить систему уравнений

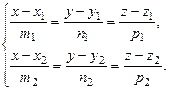
В этой системе три неизвестных (координаты точки пересечения х, у, z) и четыре уравнения, однако, если выполняются условия компланарности прямых и неколлинеарности направляющих векторов, она имеет единственное решение.

2.6.5. Расстояние от точки до прямой в пространстве.

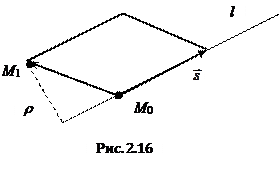Найдем расстояние от некоторой точки 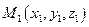до прямой l, имеющей направляющий вектор 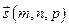и проходящей через точку 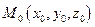. Очевидно, искомое расстояние будет являться высотой параллелограмма, построенного на векторах 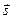и 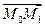. Используя геометрический смысл векторного произведения, окончательно получаем:

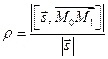. (2.22)

Чтобы найти расстояние между параллельными прямыми, нужно найти расстояние от произвольной точки первой прямой до второй прямой.

2.6.6. Расстояние между скрещивающимися прямыми.

Найдем расстояние между скрещивающимися прямыми, заданными своими каноническими уравнениями

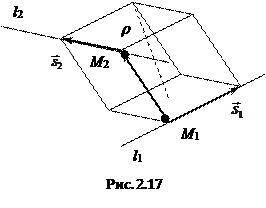
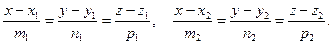
Так как прямые l₁ и l₂ скрещиваются, то векторы 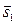, 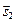и 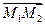некомпланарны. Очевидно, что если построить параллелепипед на векторах 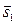, 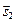и 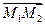(Рис. 2.17), то искомое расстояние r будет равно высоте параллелепипеда. С учетом свойств смешанного и векторного произведений получим

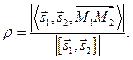(2.23)

Лекция 7.

§2.7.Кривые второго порядка на плоскости.

2.7.1. Определение. Кривой второго порядка на плоскости называется множество точек плоскости, которое описывается уравнением второго порядка, то есть

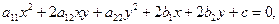(2.24)

где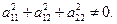

2.7.2. Определение. Канонической системой координатдля данной кривой называется декартова система координат, в которой уравнение кривой имеет наиболее простой вид.

2.7.3. Определение. Уравнение кривой в канонической системе координат называется ее каноническим уравнением.

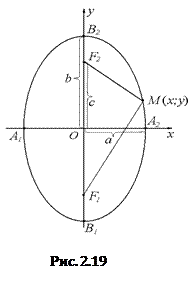
2.7.4. Эллипс.

2.7.4.1. Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, является постоянной величиной.

2.7.4.2. Каноническое уравнение эллипса.

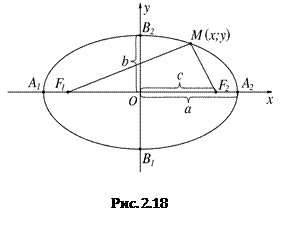
Введем на плоскости прямоугольную систему координат. Направим ось Ох вдоль линии, соединяющей фокусы F₁ и F₂, с серединой отрезка F₁F₂, а ось Оу – перпендикулярно через середину отрезка F₁F₂.

Пусть расстояние между фокусами равно 2с, а сумма расстояний от фокусов до произвольной точки равна 2а (a > c).

Тогда фокусы имеют координаты 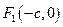и 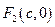, и, если 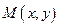– текущая точка эллипса, то расстояния от этой точки до фокусов равны длинам фокальных радиусов F₁M и F₂M: 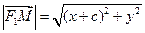и 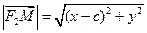. Тогда из определения эллипса

.

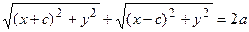Возведем обе части уравнения в квадрат:

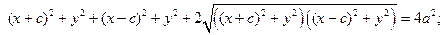
После преобразований получим:

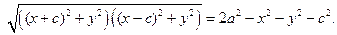
Возводя обе части уравнения в квадрат, имеем:

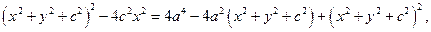
откуда

.

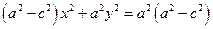Обозначая 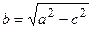, перепишем последнее уравнение в виде

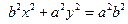, и после деления на правую часть окончательно получим

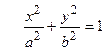. (2.25)

Это уравнение называется каноническим уравнением эллипса.

2.7.4.3. Свойства эллипса.

1. Из уравнения (2.25) следует, что 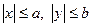, это означает, что график эллипса ограничен прямоугольником .

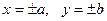2. Так как в уравнение входят только четные степени х, у, то если точка (х, у) принадлежит эллипсу, (т.е. х, у удовлетворяют уравнению), то точки (-х, у), (х, -у), (-х, -у) тоже принадлежат уравнению. Следовательно, оси Oх и Оу являются осями симметрии эллипса, точка О(0, 0) является центром симметрии.

3. Рассмотрим часть эллипса, расположенную в первом квадранте ( ). Решив уравнение относительно у, получим .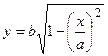

Если x = 0, то у = b; если x = а, то у = 0; у убывает при возрастании х;.

На Рис. 2.18 изображен график эллипса.

Замечание.

1. Число а называют большой полуосью эллипса, b – малой полуосью.

2. Число 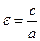называется эксцентриситетом эллипса. Этот параметр характеризует степень «сжатия» эллипса. Если 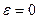(т.е. с = 0, b = а) фокусы эллипса совпадают с его центром, полуоси равны и эллипс превращается в окружность. Если 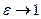( 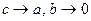) эллипс вырождается в отрезок, соединяющий фокусы.