Линейные (векторные) пространства.

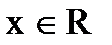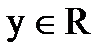Рассмотрим множество R элементов x, y, z,… для любых и которого определена сумма х+у 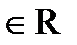и для любого действительного числа 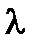определено произведение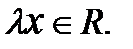

Если эти операции удовлетворяют условиям:

1. х+у = у+х ;

2. х+(у+z) = x+(y+z);

3. Существует такой элемент 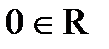, (нуль- элемент) что х+0 = х для любого ;

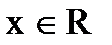4. Для каждого 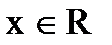существует 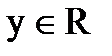такой, что х+у = 0 (у = -х, т.е. х+(-х) =0);

5. ;

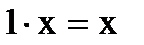6.

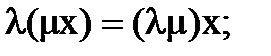
7.

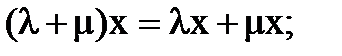
8.

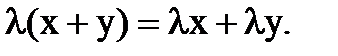
то множество 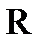называют линейным (или векторным) пространством, а его элементы x, y, z,…- векторами.

Очевидно, что множество геометрических векторов, рассмотренное ранее, является линейным пространством, а предложенное определение расширяет понятие вектора.

Линейная независимость векторов определяется через соотношение (1.15), рассмотренное ранее. Максимально возможное число n линейно независимых векторов называют размерностью этого пространства (обозначение: 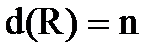) - его называют n-мерным и обозначают Rⁿ (рассматриваем конечномерные пространства). Любые n линейно независимых векторов в пространстве Rⁿ образуют базис в этом пространстве. По векторам базиса можно единственным образом разложить любой вектор пространства.

Контрольные вопросы.

1) Дайте определение линейного пространства и приведите примеры линейных пространств. Что называется вектором7