Временные (линейные) диаграммы
ПРИМЕРЫ ТИРАЖИРУЕМЫХ АЭИС ДЛЯ ПРОЕКТНОГО УПРАВЛЕНИЯ
● Подсистема «Проекты» из комплекса бизнес приложений Oracle E-Business Suite, интегрированная с системой календарно-сетевого планирования (Microsoft Project, Primavera), а также с другими подсистемами и модулями Oracle E-Business Suite. Головным разработчиком этой системы является фирма Oracle (США);
● Система 1С: Предприятие 8. Управление проектной организацией, которая является совместным прикладным решением фирм «1С» (Россия) и «ITLand Group» (Россия);
● Система Microsoft Office Enterprise Project Management Solution (решение для корпоративного управления проектами – EPM) в связке с Microsoft Office SharePoint. Разработчиком системы является всемирно известная фирма Microsoft (США), ее дистрибьютором на российском рынке – группа компаний «Проектная практика».
ПРИМЕРЫ ЛОКАЛЬНЫХ ПРОБЛЕМНО-ОРИЕНТИРОВАННЫХ ИНСТРУМЕНТАЛЬНЫХ СРЕДСТВ ДЛЯ ПРОЕКТНОГО УПРАВЛЕНИЯ
● Microsoft office Project Standard (для индивидуальной работы) и Microsoft Office Project Professional (для корпоративной работы), компания Microsoft, США. Являются архитектурными блоками указанной выше системы Microsoft Office Enterprise Project Management Solution (EPM).
● Spider Project Desktop (однопользовательская версия), Spider Project Light (версия с ограниченной функциональностью), Spider Project Desktop Plus (для корпоративной работы), компания Project Management Institute, Россия.
● Open Plan Desktop (для индивидуальной работы), Open Plan Professional (для корпоративной работы), компания Welcome System Technology, США.
● Офис управления проектами – PMO, модуль Project Management (для индивидуальной работы), модуль Portfolio Project Management (для корпоративной работы), компания «Адванта Групп», Россия.
ОСНОВНЫЕ МЕТОДЫ УПРАВЛЕНИЯ ПРОЕКТАМИ
Временные (линейные) диаграммы
| Код работы | Начало | Конец | Длительность в единицах времени | Временные периоды в единицах времени |
| 1.10 2.10 5.10 6.10 | 2.10 5.10 9.10 9.10 |          1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9

  
|
Рис. 2. Временная диаграмма хода реализации работ
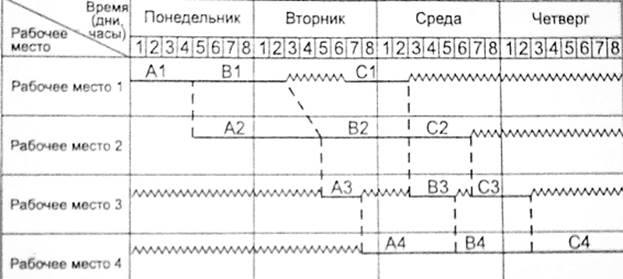
Условные обозначения:
A1-A4, B1-B4, C1-C4 – работы по изготовлению узлов A, B и C
 - простой рабочих мест
- простой рабочих мест
Рис. 3. Временная диаграмма использования исполнительских
Мощностей
Сетевое планирование и управление (СПУ)
Основные понятия и определения СПУ
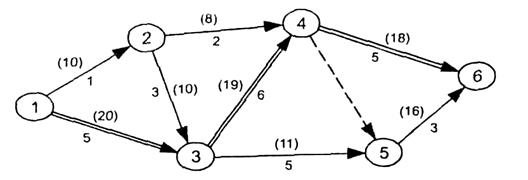
Рис. 4. Схема сетевого графика типа «дуга-работа»
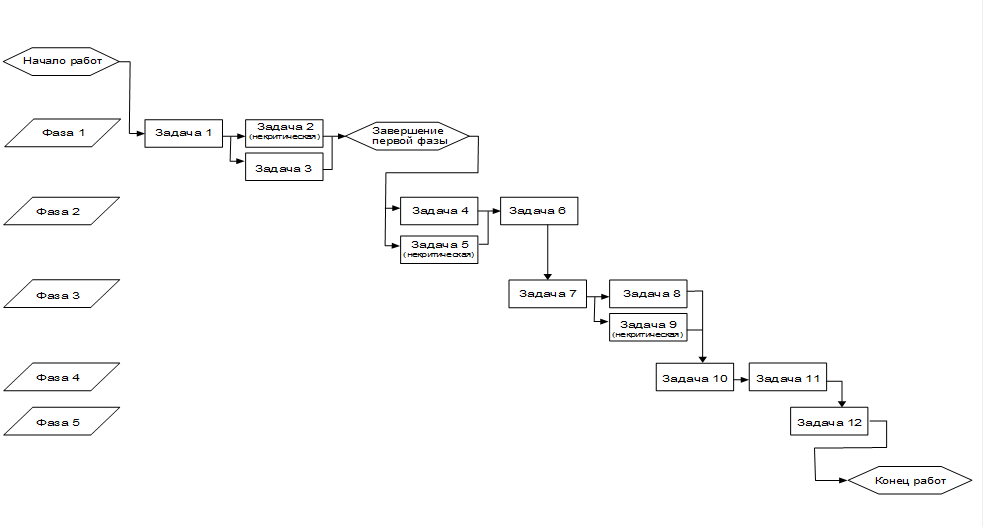 Рис. 5. Схема сетевого графика типа «вершина-работа» - диаграмма предшествования (контуры)
Рис. 5. Схема сетевого графика типа «вершина-работа» - диаграмма предшествования (контуры)
Рис. 6. Ресурсная гистограмма (график загрузки ресурса)
 Наиболее распространенные методы СПУ
Наиболее распространенные методы СПУ
1) Метод CPM (Critical Path Method) – метод критического пути.
2) Метод PERT (Program Evaluation and Review Technique) – технология оценки и просмотра плана.
3) Метод MPM (Metra Potential Method) – метод потенциальных величин.
4) Метод GERT (Graphical Evaluation and Review Technique) – технология оценки и просмотра графика.
5) Методы, реализующие оптимизацию проектов по параметрам «время – ресурсы – стоимость»: CPM-COST, PERT-COST и др.
Метод CPM (Critical Path Method) – метод критического пути:
1. Используется сеть типа «дуга – работа».
2. Сеть рассматривается как детерминированная.
Основные временные показатели сетевого графика, построенного с использованием метода CPM, определяются на основе следующих соотношений:
· Продолжительность (длина) каждой работы t(i - j), если она не задается в качестве норматива:
t(i - j) = Q(i - j) / (A(i - j)·f), (1)
где i, j – начальное и конечное события работы E(i - j);
Q(i - j) – трудоемкость работы, чел/дн.;
A(i - j)·- количество исполнителей, занятых выполнением работы E(i - j);
f– коэффициент перевода рабочих дней в календарные, f = 0,85.
· Продолжительность (длина) любого пути равна сумме продолжительностей составляющих его работ:
T(L) = Σ t(i – j) , (2)
· Продолжительность (длина) критического пути определяется на основе сравнения продолжительности всех полных путей сети и выбора максимального значения:
Ткр = max{Т(L)} , (3)
Длительность критического пути определяет длительность проекта в целом.
· Раннее время свершения события tp(i) определяется на основе сравнения продолжительности всех путей сети от начального события до данного:
tp(i) = max{T(L1(i))}, (4)
где tp(i) - раннее время свершения события i;
L1(i) – путь, предшествующий событию i.
· Позднее время свершения события tп(i) определяется на основе сравнения продолжительности всех путей сети от данного события до конечного:
tп(i) = Ткр - max{T(L2(i))} , (5)
где tп(i) – позднее время совершения события i;
L2(i) – последующий путь;
Ткр – критическое время (длина критического пути).
Для критического пути tp(i) = tп(i) , (6)
· Время раннего начала работы tрн(i - j) совпадает с ранним временем свершения события i:
tрн(i - j) = tp(i) , (7)
где tрн(i - j) – время раннего начала работы E(i – j);
tp(i) - раннее время свершения события i.
· Время позднего начала работы tпн(i - j):
tпн(i - j) = tпо(i - j) - t(i - j) , (8)
где tпн(i - j) – время позднего начала работы E(i – j);
tпо(i - j) – время позднего окончания работы E(i – j);
t(i - j) – длительность работы E(i – j).
· Время раннего окончания работы tpo(i - j):
tро(i - j) = tр(i) + t(i - j) , (9)
где tро(i - j) – время раннего окончания работы E(i – j);
t(i - j) – длительность работы E(i – j);
tр(i) – раннее время свершения события i.
· Время позднего окончания работы tпо(i - j) совпадает с поздним временем свершения события j:
tпо(i - j) = tп(j) , (10)
где tпо(i - j) – время позднего окончания работы E(i – j);
tп(j) – позднее время свершения события j.
Для критического пути характерны следующие соотношения:
tрн(i - j) = tпн(i - j) , (11)
tро(i - j) = tпо(i - j) , (12)
· Полный резерв времени работы R(i - j):
R(i - j) = tпо(i - j) – tро(i - j) = tп (j) – tр(j) - t (i - j) , (13)
· Частный (свободный) резерв времени работы r(i - j):
r(i - j) = tр(j) – tро(i - j) = tр(j) – tр(i) - t (i - j), (14)
· Резерв времени события r(i):
r(i) = tп (i) – tр(i) , (15)
В качестве единиц времени при определении показателей сетевого графика как правило используются дни, недели, декады или месяцы.
Пример сети, формируемой при использовании метода, представлен выше на рис. 4.
Метод PERT (Program Evaluation and Review Technique) – технология оценки и просмотра плана:
1. Используется сеть типа «дуга – работа».
2. Формируемая на основе данного метода сеть является стохастической (вероятностной) в отношении длительности работ и проекта в целом.
Для расчета ожидаемой продолжительности работы при использовании метода PERT принимается бета-распределениепродолжительности работ с модой (наиболее вероятным значением) в точке tнв(i - j) и концами интервала в точках tmin(i - j) и tmax(i - j). В этом случае для расчета ожидаемой продолжительности работы вместо формулы (1) применяется следующая формула:
tож(i - j) = (tmin(i - j) + 4 tнв(i - j) + tmax(i - j)) / 6(16)
где tmin(i - j) – минимальная (оптимистическая) оценка продолжительности работы;
tmax(i - j) – максимальная (пессимистическая) оценка продолжительности работы;
tнв(i - j) – наиболее вероятной продолжительности работы.
На основе четырех оценочных показателей длительности работ (tmin(i - j), tнв(i - j), tmax(i - j) и tож(i - j) ) могут быть сформированы четыре основные версии сетевой модели с разными по длительности критическими путями, а, следовательно, разными оценками длительности проекта в целом ‒ минимальной (оптимистической), наиболее вероятной, максимальной (пессимистической) и ожидаемой (Tmin, Tнв, Tmaxи Tож) и сроков его реализации.
Сетевая модель, сформированная на основе результатов расчета ожидаемой длительности задач проекта, может рассматриваться в качестве обобщающей, а остальные модели – как дополняющие локальные.
Для стохастической сети, основанной на применении метода PERT необходимо определитьразмах колебаний продолжительности работы под влиянием неопределенности (разброс продолжительности). Для бета-распределения вероятностей разброс в этом случае определяется как разность между пессимистическим (максимальным) и оптимистическим (минимальным) значением длительности:
а) для работы проекта:
Δ t(i - j) = tmax(i - j) - tmin(i - j) (17)
а) для проекта в целом:
Δ T = Tmax - Tmin(18)
Будем называть данную оценку разброса длительности экспертной. Относительный недостаток экспертной оценки разброса заключается в том, что разброс длительности работы (проекта) в связи с действием фактора неопределенности может превышать непосредственно величину ожидаемой их длительности или, по крайней мере, быть соизмеримым с ней. Это делает оценку разброса длительности проекта и сроков его реализации недостаточно корректной. В то же время можно утверждать, что вероятность попадания длительности проекта в «интервал разброса» практически равна 1 (если не принимать во внимание форс-мажорные обстоятельства).
График бета-распределения вероятностей представлена на рис. 7.
Если мода и математическое ожидание близки по своему значению, то можно воспользоваться статистическими оценками разброса длительностей, принятыми для нормального распределения вероятностей, – среднеквадратическим отклонением и дисперсией длительности работы, а также проекта в целом. Принимается, что размах колебаний (разброс) длительности работы под влиянием неопределенности равен шести среднеквадратическим отклонениям, т.е. среднеквадратическое отклонение может быть определено по формуле:
σ(i - j) =(tmax (i - j) - tmin (i - j)) / 6 (19)
Дисперсия длительности работы в этом случае равна:
σ(i - j)2=[(tmax(i - j) - tmin(i - j)) / 6] 2 (20)
Дисперсия длительности проекта в целомопределяется как сумма дисперсий критических работ. Среднеквадратическое отклонение длительности реализации проекта определяется путем извлечения квадратного корня из величины дисперсии. На основе этого по правилу «трех сигм»[1] может быть определен возможный разброс длительности выполнения проекта в целом.
Статистическая оценка разброса длительности проекта заметно меньше экспертной в результате того, что попадание длительности проекта в «интервал разброса» при отсутствии форс-мажорных обстоятельств гарантируется с вероятностью 0,997 (что меньше 1, но представляется вполне достаточным). Нетрудно видеть, что для работ проекта экспертный и статистический разброс длительности совпадают, поэтому меньшее значение статистического разброса длительности проекта в целом можно интерпретировать также на основе гипотезы погашения запаздывания одних критических работ досрочным выполнением других.
Наряду с разбросом длительности выполнения работ и проекта в целом аналогичным образом определяется разброс календарных сроков их выполнения.
Примечание: некоторые специалисты рекомендуют применять правило «двух сигм», что гарантирует попадание длительности проекта в заметно меньший доверительный интервал разброса с вероятностью 0,954.
График нормального распределения вероятностей представлен на рис. 8.
Пример сети, формируемой с использованием метода PERT, показан выше на рис. 4 (внешне она не отличается от сети, построенной с использованием метода CPM).
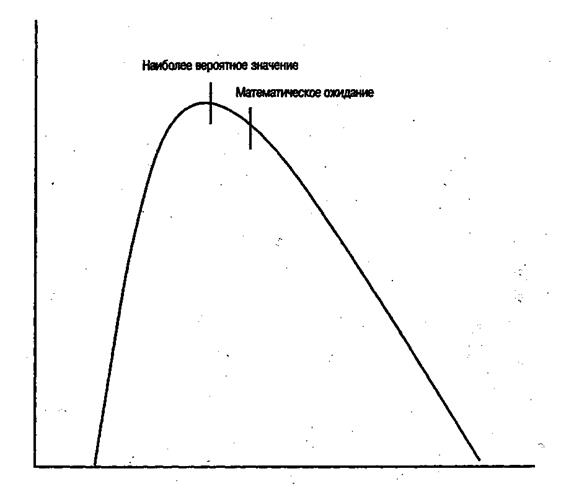
Рис. 7. График бета-распределения вероятностей

Рис. 8. График нормального распределения вероятностей
Метод MPM (Metra Potential Method) – метод потенциальных величин:
1. Используется сеть типа «вершина – работа» (диаграмма предшествования), в которой множество вершин, соответствующих работам (они обозначаются геометрическими фигурами), связанны линиями (дугами), представляющими взаимосвязи между работами.
2. Канонический подход к построению сети типа «вершина – работа» не предполагает отображения событий. Тем не менее, в формируемую сетевую модель могут быть включены наиболее важные события проекта (начало и конец работ, завершение и начало отдельных этапов и т.п.).
3. Сеть рассматривается как детерминированная. Основные временные показатели сетевого графика, построенного с использованием метода MPM, определяются, как и при использовании метода CPM, по формулам (1 – 15). Пример сети, формируемой с применением метода MPM, показан выше на рис. 5.
Метод MPM используется в качестве базового в программном продукте Microsoft Project, который используется при выполнении лабораторной работы.
Метод GERT (Graphical Evaluation and Review Technique) – технология оценки и просмотра графика.
В данном методе стохастический подход (см. выше метод PERT)распространяется на топологию сети, то есть на состав работ и связи между ними. По этой причине в сетевой модели допускаются альтернативные работы.
Кроме того, в сети данного вида допускаются петли, то есть возврат к выполненным ранее работам, что дает возможность отражать при моделировании периодически повторяющиеся производственные операции.
Пример сети, формируемой с применением метода GERT, показан на рис. 9.
Методы, реализующие оптимизацию проектов по параметрам «время – ресурсы – стоимость»: CPM-COST, PERT-COST и др.
Все рассмотренные выше методы СПУ позволяют оптимизировать сетевую модель проекта по критериям времени (минимизация) и ресурсов, главным образом, трудовым (минимизация, выравнивание загрузки). Методы CPM-COST, PERT-COST и некоторые другие позволяют также оптимизировать исходный вариант сети по критерию стоимости (бюджета) проекта, осуществляя ее минимизацию или обеспечивая равномерное расходование средств.
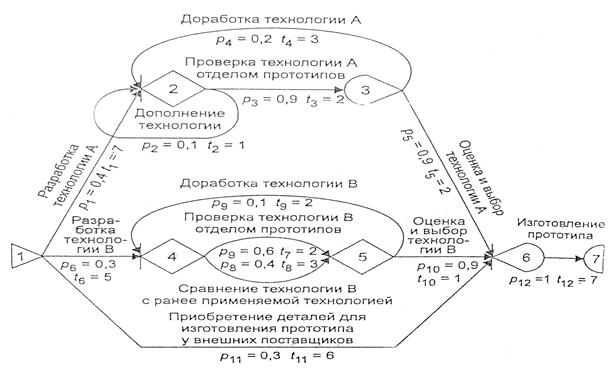
Рис. 9. Пример сетевого графика, сформированного по методу GERT
Дата добавления: 2016-03-10; просмотров: 2466;
