Квадратичные формы.

Квадратичной формой 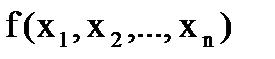переменных х₁, х₂,…,х_n называют многочлен второй степени относительно этих переменных, не содержащий членов нулевой и первой степени.

При n=2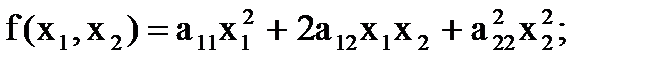

при n=3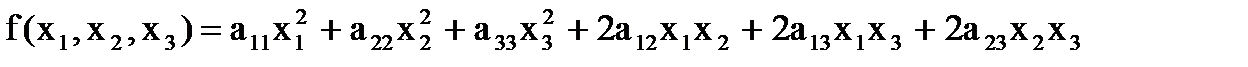

А = 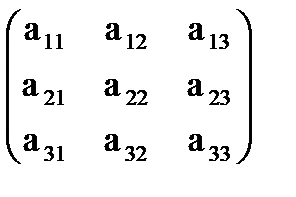, где a_ij = a_ji называют матрицей квадратичной формы 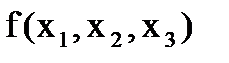. Матрица А симметрическая, собственные значения её- действительные числа.

Пусть 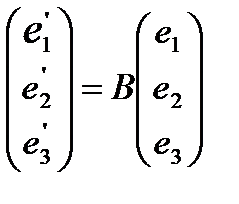нормированные собственные векторы в ортонормированном базисе е₁, е₂,е₃. Векторы 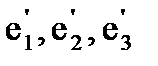также образуют ортонормированный базис. 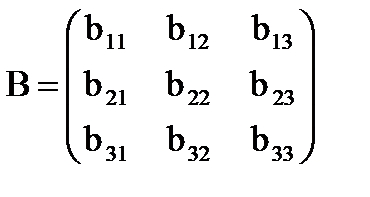- матрица перехода о т базиса е₁,е₂,е₃ к базису 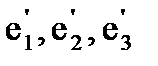. Формулы преобразования координат при переходе к новому ортонормированному базису примут вид: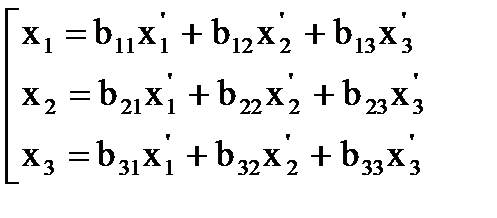

Переходя к новым координатам получаем квадратичную форму 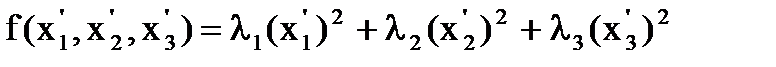не содержащую членов с произведениями переменных. Квадратичная форма 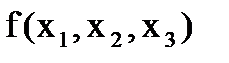приведена к каноническому виду с помощью ортогонального преобразования. (Предполагалось, что среди собственных чисел матрицы А нет кратных. В случае, если они есть, задача решается немного сложнее).

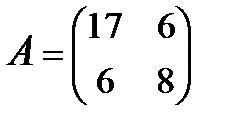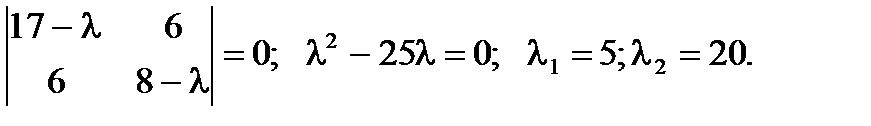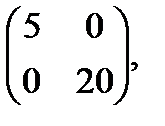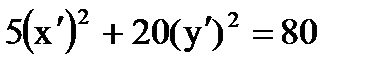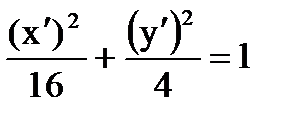Пример: Привести к каноническому виду уравнение линии 17х²+12ху+8у²=80. В левой части - квадратичная форма с матрицей . Найдём собственные значения: Матрица преобразования принимает вид квадратичная форма преобразуется к канонической, а уравнение линии к виду или - (каноническое уравнение эллипса).

Контрольные вопросы.

1) Что называют квадратичной формой?