Глва 2. Введение в математический анализ.
2.1. Функция. Напомним несколько необходимых понятий. Переменной называют величину, которая принимает различные значения. Постоянной – величину, значение которой остается неизменным. Постоянную величину можно рассматривать, как частный случай переменной. Областью изменения переменной величины называют совокупность всех ее значений. Интервалом называют совокупность всех чисел х, заключенных между данными числамиа и b (a < b) причем сами а и b не принадлежат рассматриваемой совокупности хÎ(а,b) (открытый интервал). Частный случай –хÎ (–¥, ¥). Отрезок (закрытый интервал) – совокупность всех х заключенных между а и b включая границы хÎ[a, b]. Если одна из границ (например а) входит, а другая не входит в рассматриваемую область хÎ [a, b)– полузакрытый интервал. Окрестностью точки х0 называют произвольный интервал, содержащий х0 внутри себя (а < x0 < b). Если 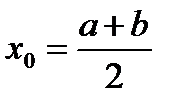 , ее называют центром, а
, ее называют центром, а 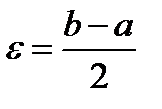 – радиусом окрестности. ( e окрестность).
– радиусом окрестности. ( e окрестность).
Если каждому значению переменной х, принадлежащему некоторой области, по определенному правилу ставится в соответствие значение другой переменной у, то говорят, что у есть функция от х (символическая запись: y = f(x) или y = y(x) и т.п.); х называют независимой переменной (аргументом). Совокупность значений х называют областью определения (существования), а совокупность значений у – областью изменения функции.
Рассмотрим основные способы задания функции.
1. Табличный способ (часто используется в экспериментальных исследованиях) заключается в составлении таблицы, в которой в соседних клетках одного столбца (строки) расположены соответствующие значения аргумента и функции, например:
| Х | х1 | х2 | ….. | xi | ….. | хn |
| У | у1 | у2 | ….. | yi | ….. | yn |
2. Графический способ. Значения х и у рассматриваются как координаты точек. Совокупность точек плоскости хОу, абсциссы которых суть значения аргумента, а ординаты – значения функции, называют графиком функции. Если известен график, функция задана графически.
3. Аналитический способ. Аналитическим выражением называется символическое обозначение математических операций, производимых в определенной последовательности над постоянными и переменными величинами (например 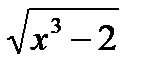 ; lg sinx2 и т.д.).
; lg sinx2 и т.д.).
Если у = f(x) и f(x) обозначает аналитическое выражение, говорят, что функция задана аналитически (например 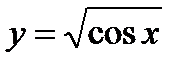 ).
).
Элементарной функция называется, если ее можно задать одной формулой вида у = f(x), где выражение, стоящее справа, составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. (Функцию от функции называют сложной функцией).
Напомним, что основными элементарными функциями (их свойства и графики полагаем известными из курса средней школы) являются:
1) Степенная функция: у = хa,гдеa Î R, х >0
2) Показательная функция: у = ах,гдеa > 0, a ¹ 1
3) Логарифмическая функция: у = logax,гдеа > 0, a ¹ 1
4) Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, у = cosec x
5) Обратные тригонометрические функции: y = arcsin x, y = arccos x,
y = arctg x, y = arcctg x, y = arcsec x, у = arccosec x
Контрольные вопросы.
1) Что называется функцией?
2) Что называется областью определения функции?
3) Перечислите основные элементарные функции.
Тест 14.
1) В каком из основных способов задания функции является
а) табличный способ;
б) графический;
в) аналитический.
2) Какая из функций имеет область определения в интервале 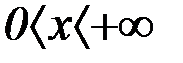 ?
?
а) показательная функция у=ах, а>0;
б) логарифмическая функция, у= logax, а>0;
в) тригонометрические функции у=sinx, y=cosx, y=tgx, y=secx, y=ctgx, y=cjsecx.
г) отборные тригонометрические функции y=arsinx, y=arccosx, y=arcctgx.
2.2. Предел. Непрерывность функции. Переменную величину х называют упорядоченной, если известна область D изменения ее и про каждое из двух любых значений можно сказать, какое предыдущее и какое последующее.
Рассмотрим упорядоченную переменную, изменяющуюся специальным образом, определяемым термином «Переменная величина стремится к пределу».
Число а называют пределом переменной х, если для всякого сколь угодно малого положительного e можно указать такое значение х, начиная с которого все последующие значения будут удовлетворять неравенству |x –а|<e. В этом случае говорят, что х стремится к а (символически х ® а или lim x = a).
Геометрическая интерпретация (рис.2.1): постоянная а есть предел переменной х, если для любой сколь угодно малой e– окрестности точки а найдется такое значение х, что все точки, соответствующие последующим
| Рис. 2.1 |
| X |
| · |
| a |
| a - ε |
| a + ε |
| X |
| Рис. 2.1. |
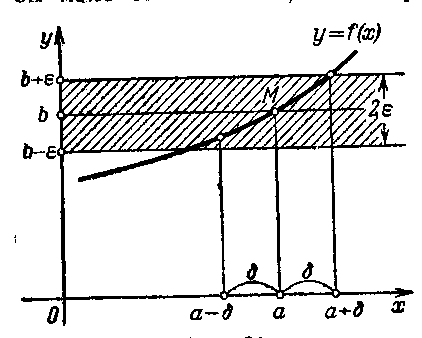
| Рис. 2.2 |
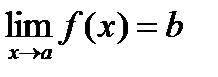 . Геометрическая интерпретация (рис.2.2.) – для всех точек х отстоящих от а не более чем на d, точки М графика функции у = f(x) лежат внутри полосы шириной 2e, ограниченной прямыми у = b –eи y = b + e.
. Геометрическая интерпретация (рис.2.2.) – для всех точек х отстоящих от а не более чем на d, точки М графика функции у = f(x) лежат внутри полосы шириной 2e, ограниченной прямыми у = b –eи y = b + e.
Если х < а их ® а, то пишут х ® а – 0; если х > а и х ® а – пишут х ® а + 0. Числа 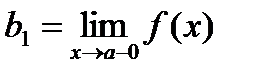 и
и 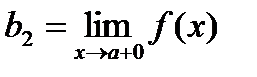 называют левым и правым пределом функции f(x) в точке а. Если b1 и b2 существуют и равны, т.е. b1 = b2 = b, то b и будет пределом в точке а в смысле данного выше определения. Отметим, что для существования предела в точке а не требуется, чтобы функция была определена в точке а. (Рассматриваются значения х в окрестности точки а, отличные от а).
называют левым и правым пределом функции f(x) в точке а. Если b1 и b2 существуют и равны, т.е. b1 = b2 = b, то b и будет пределом в точке а в смысле данного выше определения. Отметим, что для существования предела в точке а не требуется, чтобы функция была определена в точке а. (Рассматриваются значения х в окрестности точки а, отличные от а).
Говорят, что функция f(x) стремится к пределу b при х ® ¥, если для всякого e > 0 можно указать такое N > 0, что для всех х удовлетворяющих условию |x| > N будет выполняться неравенство |f(x) – b| < e.
Функция f(x) стремится к бесконечности при х ® а, (является бесконечно большой при х ® а) если для всякого M > 0, как бы велико оно ни было, можно найти такое d > 0, что для всех х ¹ а и удовлетворяющих условию |x – a| < d имеет место |f(x)| > M, т.е. 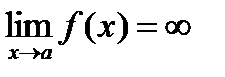 (При этом возможно как
(При этом возможно как 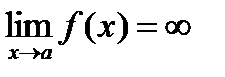 , так и
, так и 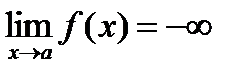 ). Отметим, что функция может и не стремиться к конечному пределу при х ® а или х ® ¥. Примеры: у = sin x не имеет предела при х ® ¥, а у = sin 1/x – при х ® 0.
). Отметим, что функция может и не стремиться к конечному пределу при х ® а или х ® ¥. Примеры: у = sin x не имеет предела при х ® ¥, а у = sin 1/x – при х ® 0.
Функция a(х) называется бесконечно малой при х ® а или х ® ¥, если 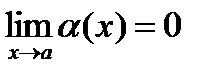 или
или 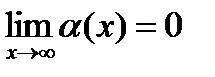 .
.
Говорят, что если a(х) и b(х) – бесконечно малые при х ® а, и:
1)  (или
(или 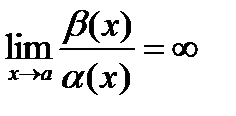 ) – то a – бесконечно малая высшего порядка по сравнению с bи пишут a = 0 (b).
) – то a – бесконечно малая высшего порядка по сравнению с bи пишут a = 0 (b).
2) 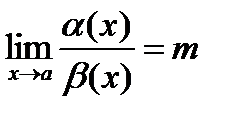 , где m – число отличное от нуля, то a и b бесконечно малые одного порядка. Если m = 1, a и b – эквивалентные бесконечно малые, что можно записать используя уже знакомый символ эквивалентности: a ~b.
, где m – число отличное от нуля, то a и b бесконечно малые одного порядка. Если m = 1, a и b – эквивалентные бесконечно малые, что можно записать используя уже знакомый символ эквивалентности: a ~b.
3) 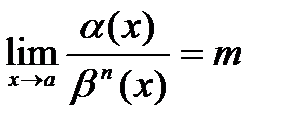 , где m- число отличное от нуля, то a- бесконечно малая n-го порядка по сравнению с b (т.е. a~bn).
, где m- число отличное от нуля, то a- бесконечно малая n-го порядка по сравнению с b (т.е. a~bn).
Отметим, что предел отношения бесконечно малых не изменится при замене их (или одной из них) эквивалентными бесконечно малыми. Это позволяет упростить решение многих задач теории пределов.
Аналогично сравниваются и бесконечно большие функции.
Связь между бесконечно малыми и бесконечно большими функциями определяется теоремой: если a(х) - бесконечно малая при х® а, то функция f(x)=1/a(x) - бесконечно большая при х® а, и обратно, если f(x) - бесконено большая при x ® а, то a(x)=1/f(x) - бесконечно малая при х® а
Дата добавления: 2016-04-14; просмотров: 1508;
