Линейные преобразования.
Говорят, что в линейном пространстве R задано преобразование А, если каждому вектору 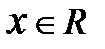 по некоторому правилу ставится в соответствие вектор А
по некоторому правилу ставится в соответствие вектор А 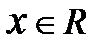 . Преобразование называют линейным, если для любых х и у и любого действительного числа
. Преобразование называют линейным, если для любых х и у и любого действительного числа 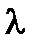 выполняются равенства А(х+у)=Ах+АуиА(
выполняются равенства А(х+у)=Ах+АуиА( 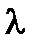 х)=
х)= 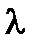 Ах (его можно рассматривать как линейное преобразование координат точки или вектора- переход к другим координатам). Пусть в пространстве R3 с базисом
Ах (его можно рассматривать как линейное преобразование координат точки или вектора- переход к другим координатам). Пусть в пространстве R3 с базисом 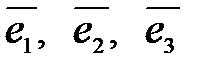 задано линейное преобразование А. Каждый из векторов
задано линейное преобразование А. Каждый из векторов 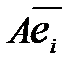 можно единственным образом разложить по векторам базиса
можно единственным образом разложить по векторам базиса
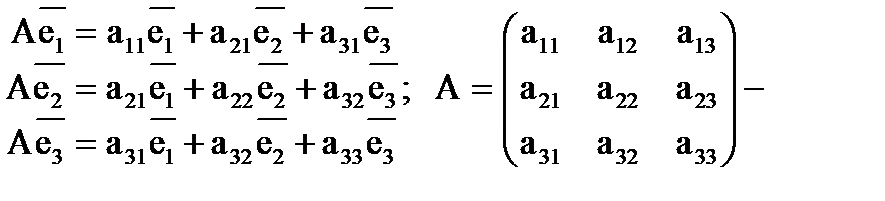 матрица линейного преобразования А в базисе
матрица линейного преобразования А в базисе 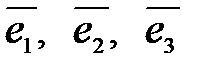 . (аналогично - в пространстве
. (аналогично - в пространстве 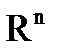 при
при 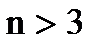 ).
).
Действия над линейными преобразованиями сводятся к действиям над их матрицами. Например, если вектор 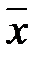 переводится в вектор
переводится в вектор 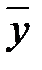 преобразованием А, а вектор
преобразованием А, а вектор 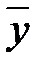 переводится в вектор
переводится в вектор 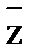 преобразованием В, это равносильно преобразованию С, переводящему вектор
преобразованием В, это равносильно преобразованию С, переводящему вектор 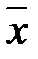 в вектор
в вектор 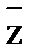 (его называют произведением составляющих преобразований).
(его называют произведением составляющих преобразований).
Матрица этого линейного преобразования С = ВА.
Пример: Даны два линейных преобразования
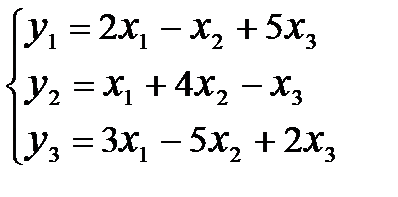 и
и 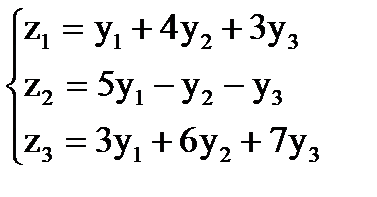 или
или 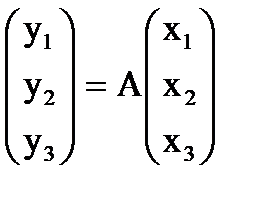 и
и 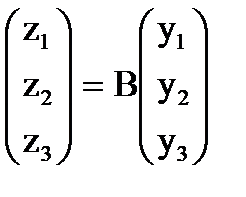 , где
, где 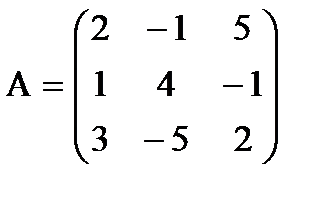 и
и 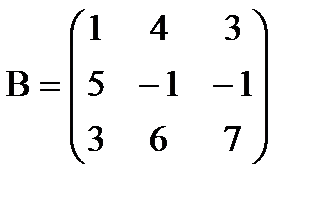
Искомое преобразование С определится произведением А и В
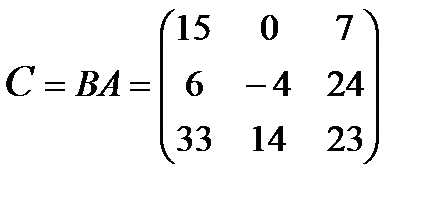 и
и 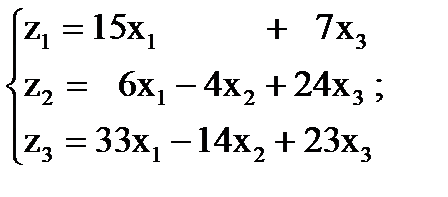
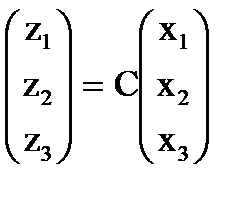 .
.
Вид матрицы линейного преобразования определяется выбором базиса. Если за базис принять совокупность собственных векторов (см. 1.5.5), то матрица линейного преобразования принимает диагональный вид, причём на главной диагонали стоят собственные значения. Например, в R2 это матрица 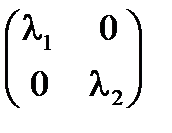 , линейное преобразование:
, линейное преобразование: 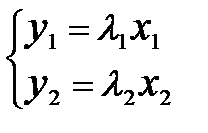 .
.
Число собственных векторов может быть меньше размерности пространства. В этом случае простейшая матрица линейного преобразования формируется иначе. Рассмотрим в n-мерном базисе преобразование Fвида:
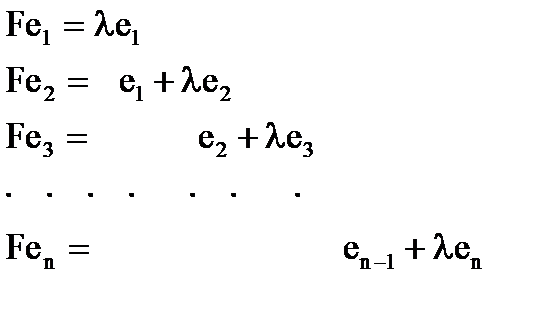
Матрица этого преобразования в базисе 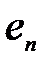 обозначается
обозначается 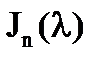 и называется n-мерной жордановой клеткой соответствующей числу
и называется n-мерной жордановой клеткой соответствующей числу 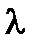 .
.

Говорят, что матрица А имеет каноническую жорданову форму, если по главной диагонали её расположены жордановы клетки, а все остальные элементы - нули.

При этом возможно, что 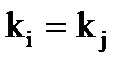 или
или 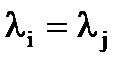 для некоторых номеров i и j.
для некоторых номеров i и j.
Контрольные вопросы.
1) Что называют линейным преобразованием? 2) Что называют матрицей линейного преобразования? 3) Чем определяется вид матрицы линейного преобразования?
Дата добавления: 2016-04-14; просмотров: 1594;
