Прямая на плоскости.
Всякое уравнение первой степени (линейное) относительно х и у вида
Ах + Ву + С = 0 (1.29),
(А, В, С – постоянные величины, причем А2+ В2 ¹ 0) определяет на плоскости некоторую прямую и называется общим уравнением прямой. Рассмотрим частные случаи:
1. А ¹ 0, В ¹ 0, С = 0. Очевидно, что Ах + Ву = 0 – уравнение прямой проходящей через начало координат.
2. А = 0, В ¹ 0, С ¹ 0. Уравнение (1.29) преобразуется к виду у = – С / В = b и определяет прямую параллельную оси Ох (При С = 0 => b = 0 и прямая совпадает с осью Ох)
3. А ¹ 0, В = 0, С ¹ 0. Уравнение (1.29) принимает вид х = – С /А = а и определяет прямую параллельную оси Оу (При С = 0 => a = 0 и прямая совпадает с осью Оу)
4. Если В ¹ 0, то, разрешив (1.29) относительно у, получим уравнение вида
у = кх + b (1.30)
(к = – А / В, b = – С / В), называемое уравнением с угловым коэффициентом, (к = tga, где a – угол между прямой и положительным направлением оси Oх. b – ордината точки пересечения прямой с осью Оу).
5. Если в (1.29) С ¹ 0, то разделив обе части равенства на -С, получим уравнение вида (х / а) – (у / b) = 1 (1.31)
( а = – С/А; b = – С/В, называемое уравнением прямой в отрезках (|a| и|b| – длины отрезков, отсекаемых на осях Ох и Оу от начала координат).
6. Умножив обе части (1.29) на 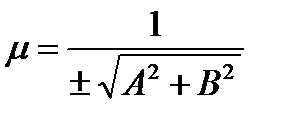 (нормирующий множитель, знак которого выбирают из условия m С < 0) получим нормальное уравнение прямой х соs j + y sin j – p = 0 (1.32),
(нормирующий множитель, знак которого выбирают из условия m С < 0) получим нормальное уравнение прямой х соs j + y sin j – p = 0 (1.32),
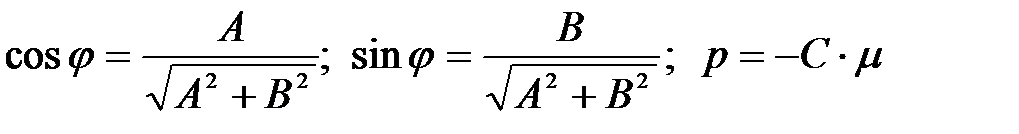 ,гдер – длина перпендикуляра, опущенного из начала координат на прямую, а j – угол между ним и осью Ох.
,гдер – длина перпендикуляра, опущенного из начала координат на прямую, а j – угол между ним и осью Ох.
Используя предложенные формы уравнений прямой можно получить следующие соотношения:
Острый угол между прямыми у = к1х + b1, у = к2х + b2, определится по формуле: 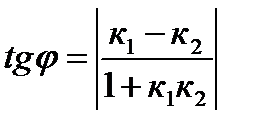 (1.33)
(1.33)
Из нее легко получить условие параллельности к1 = к2 (1.34) и
перпендикулярности к2 = – 1 / к1 (1.35) прямых.
Уравнение прямой, проходящей через точку М0(х0, у0) под заданным углом aк оси Ох (с заданным угловым коэффициентом к = tga) примет вид
у – у0 = к (х – х0) (1.36),
а уравнение прямой, проходящей через заданные точки М1(х1, у1) и М2(х2, у2).
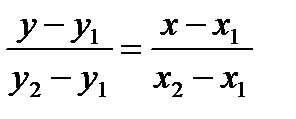 (1.37)
(1.37)
Найти координаты точки пересечения прямых можно решив систему уравнений, определяющих эти прямые.
Расстояние от точки М0(х0, у0) до прямой Ах + Ву + С = 0 определяется по формуле: 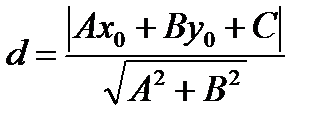 (1.38)
(1.38)
Деление отрезка в данном отношении. Приведем еще одно соотношение, часто используемое в аналитической геометрии. Проведем прямую через точки А(х1, у1)иВ(х2, у2). Всякая третья точка С(х, у) прямой делит отрезок АВ в некотором отношении l = ± АС / СВ (если точка С лежит внутри отрезка АВ, то l > 0, если вне, то l < 0). Координаты точки С определяются выражениями:
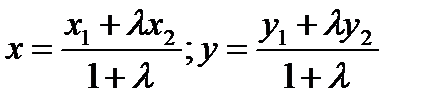 (1.39) (l = 1, если точка С – середина отрезка).
(1.39) (l = 1, если точка С – середина отрезка).
Контрольные вопросы.
1) Каков характерный признак, отличающий уравнение прямой в декартовой системе координат от уравнений других линий? 2) Как расположена прямая относительно декартовой системы координат, если в её уравнении отсутствует: а) свободный член; б) одна из координат; в) одна из координат и свободный член? 3) Как вычислить угол между двумя прямыми? Каковы условия параллельности и перпендикулярности прямых? 4) Как можно найти угловой коэффициент прямой, если известно её общее уравнение? Можно ли найти угловой коэффициент прямой, не составляя её уравнения, если известны две её точки? Если да, то как это сделать? 5) Напишите уравнение прямой проходящей: а) через данную точку в данном направлении; б) через две данные точки. 6) Напишите формулы, выражающие координаты точки, делящей отрезок в данном отношении, через координаты его концов. 7) Напишите формулы, выражающие координаты: а) середины отрезка через координаты его концов; б) центра тяжести треугольника через координаты его вершин. 8) Напишите формулу, выражающую площадь треугольника через координаты его вершин. 9) Как найти расстояние от данной точки до прямой, заданной уравнением общего вида? 10) Напишите уравнения осей декартовой системы координат. Тест 9. 1) Вычислить площадь треугольника с вершинами А(2,0), В(5,3), С(2,6) и указать верный ответ: а) 9 кв.ед., б) 8 кв. ед. 2) Определить параметры k и b для каждой из прямых: 1) 2) 1) а) 3) а) 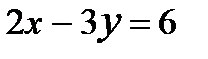 ;
;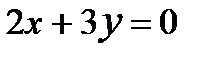 ; 3)
; 3) 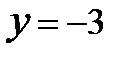 ; 4)
; 4) 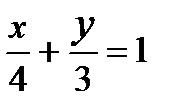 и указать верные ответы:
и указать верные ответы: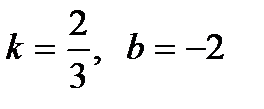 ; б)
; б) 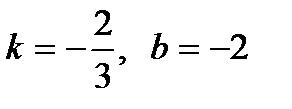 ; 2) а)
; 2) а) 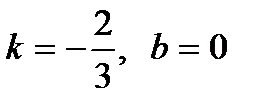 ; б)
; б) 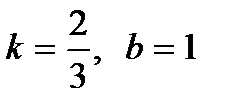 ;
;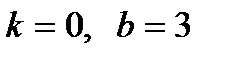 ; б)
; б) 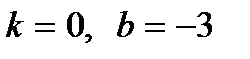 ; 4) а)
; 4) а) 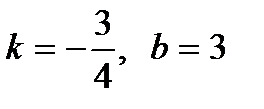 ; б)
; б) 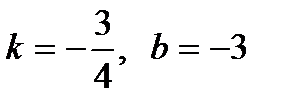 .
.
Дата добавления: 2016-04-14; просмотров: 1672;
