Нормальное распределение на плоскости.

Из всех законов распределения системы двух СВ наибольшее распространение на практике имеет нормальное распределение. Рассмотрим нормальное распределение для системы двух независимых СВ

f₁(x)= 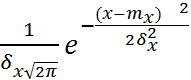f₂(y)=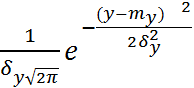

следовательно:

f(x,y)=f1(x)f2(y)=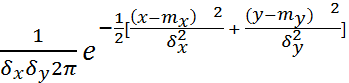

если центр рассеивания совпадает с началом координат, то есть m_x=m_y=0 и следовательно f(x,y)=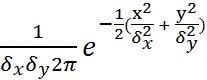

Последнее выражение называется канонической формой нормального распределения на плоскости.

Для выяснения вида поверхности распределения будем применять метод сечения.

Условие: Z=Z₀=const

Z= f(x,y)= 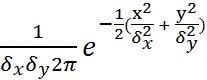,т.е.

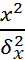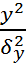+ =k² (k=const),преобразуем последнее к виду

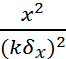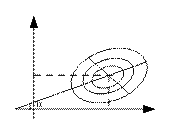
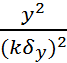+ =1- уравнение эллипса, главные полуоси которого пропорциональны 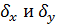и совпадают соответственно с осями Ox и Oy, а центр находится в начале координат. Т.к. kможет меняться от 0 до ∞, то мы имеем семейство подобных и одинаково расположенных эллипсов. Они называются эллипсами разной плотности или эллипсами рассеивания.

Пересекая поверхность распределения плоскостями параллельными координатами плоскости yOz или xOz мы будем получать кривые, подобные кривым нормального распределения.

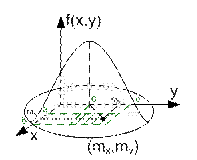
если m_x 0 и m_y 0 имеем поверхность полученную параллельным переносом описанной выше поверхности с осевой линией пересекающей плоскость xOy в точке (m_x m_y).

Подсчитаем вероятность попадания точки в прямоугольник со сторонами, параллельными осями координат.

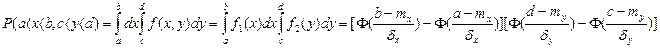
Рассмотрим теперь нормальное распределение на плоскости для зависимых СВ

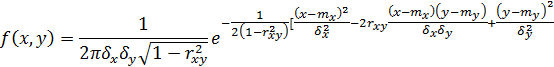
Закон распределения зависит от пяти параметров: m_x, m_y, 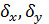,r_xy .

m_x, m_y – МОЖ СВ X и Y соответственно 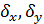- СКО СВ X и Yсоответственно r_xy – коэффициент корреляции СВ X и Y.

Рассмотрим уравнение

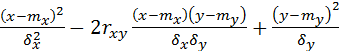= k²

Анализируя уравнение обычным методами аналитической геометрии, убеждаемся в том, что оно представляет эллипс, центр которого находится в точке с координатами (m_x, m_y), а оси симметрии такого эллипса составляют с осью Ox углы, определяемые уравнением

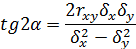
Уравнение дают два значения углов α₁ и α₂

различающихся по величине . Из уравнения следует, что ориентация эллипсов рассеивается относительно координатных осей, находится в прямой зависимости от коэффициента корреляции 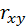системы (X,Y) . Если X и Y не коррелированны ( 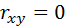), то главные оси параллельны координатным осям.

Используя логику вышеприведенного не сложно получить характеристики условного закона распределения

M[Y/X=x]=m_y(x)=m_y+r_xy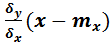

M[X/ Y =y]=m_x(y)=m_x+r_xy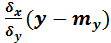

= _; =

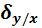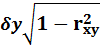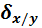
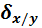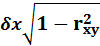
Формулы показывают, что линии регрессии Y по X и X по Yв случае нормального распределения являются прямыми линиями и проходят через точку (mx ,my)

Y=my - 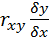(x-mx); X=mx - 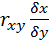(y-my).

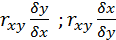- коэффициенты линии регрессии