Теоремы о дисперсиях.
Теорема 1.Дисперсия суммы СВ равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими
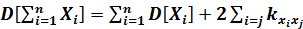
Следствие 1.Дисперсия суммы некоррелированных СВ равна сумме дисперсий слагаемых
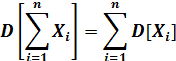
Теорема 2. Дисперсия произведения двух независимых случайных величин вычисляется по формуле.
D[XY]=D[X]D[Y]+mx2D[Y]+ my2D[X]
Следствие. Дисперсия произведения независимых центрированных СВ равно произведению их дисперсии.
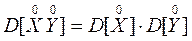
ТЕМА 5. ЗАКОН БОЛЬШИХ ЧИСЕЛ И ПРЕДЕЛЬНЫЕ
ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
Предельные теоремы теории вероятностей.
Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками СВ и случайных событий при большом числе испытаний над ними, а также касающихся предельных законов распределения, объединяются под общим названием предельных теорем теории вероятностей.
В настоящей лекции мы познакомимся с двумя типами предельных теорем: законом больших чисел и центральной предельной теоремой.
Закон больших чисел, занимающий важнейшее место в теории вероятностей, является связующим звеном между теорией вероятностей как математической наукой и закономерностями случайных явлений при массовых наблюдениях над ними.
2. Закон больших чисел: теорема Чебышева, теорема Маркова.
Рассмотрим СВ Х, МОЖ которой mх и дисперсия Dх.
Неравенство Чебышева утверждает: вероятность того, что
отклонение случайной величины от ее МОЖ будет по абсолютной величин не меньше любого положительного числа 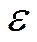 , ограничена сверху величиной
, ограничена сверху величиной 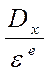 .
.
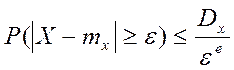
Доказательство: 1. Пусть СВ Х дискретное с рядом распределения
| Хк | Х1 | Х2 | … | Хn |
| Рк | Р1 | Р2 | … | Рn |
тогда дисперсия СВ Х 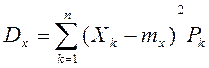 .
.
Очевидно, что слагаемые этой суммы не отрицательны. Отбросим те слагаемые, у которых 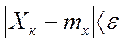 ,вследствие чего сумма может только уменьшиться, т.е.
,вследствие чего сумма может только уменьшиться, т.е. 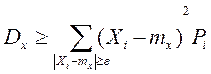 , заменим
, заменим 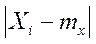 через
через 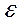
 , то после этой замены å может только уменьшиться.
, то после этой замены å может только уменьшиться. 

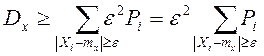 , но
, но 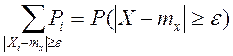 .
.
Т.о. 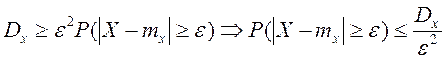
2. Пусть СВ Х непрерывна с плотностью распределения f(х).
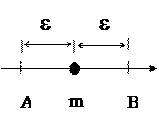 Тогда
Тогда 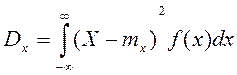 выделим на числовой оси
выделим на числовой оси
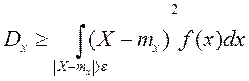 , заменяя
, заменяя 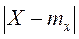 через
через 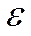 , опять уменьшаем величину интеграла
, опять уменьшаем величину интеграла 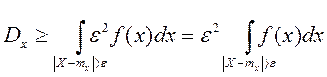 , но
, но
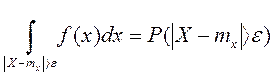 , следовательно
, следовательно 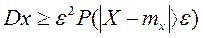 .
.
Здесь знак ³ заменен знак >, так как для непрерывной СВ вероятность точного равенства рана 0.
Теорема ЧЕБЫШЕВА. При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений СВ, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию.
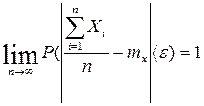
Доказательство: рассмотрим СВ 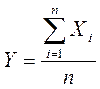
 Применим к СВ Y неравенства
Применим к СВ Y неравенства 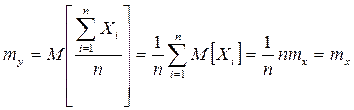
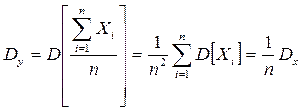
Чебышева 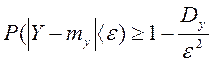 или
или 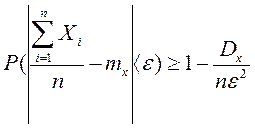 .
.
Перейдя к пределу, учитывая, что Р£1 и 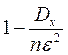 ®1 при n®¥
®1 при n®¥
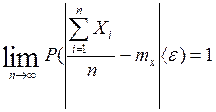 Теорема доказана.
Теорема доказана.
Обобщенная теорема Чебышева. При неограниченном увеличении числа независимых испытаний над СВ, имеющим ограниченные дисперсии, среднее арифметическое наблюдаемых значений сходится по вероятности к среднему арифметическому МОЖ этих величин, т.е.
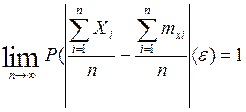
Доказательство: Рассмотрим СВ 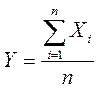

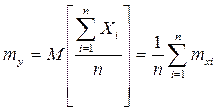
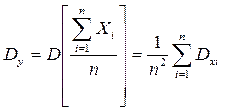
Применяя к СВ Y неравенство Чебышева получим 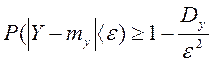 или
или 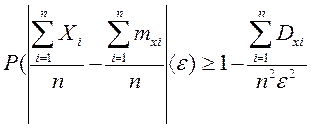 .
.
Из ограниченности дисперсий следует, что существует такое постоянное С, для которого Dxi<C(i=1,2,…,n), поэтому 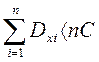 , подставив последнее в формулу
, подставив последнее в формулу 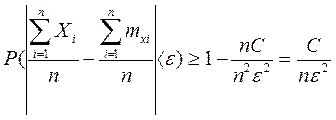 , перейдя к пределу получим доказываемое, Теорема доказана.
, перейдя к пределу получим доказываемое, Теорема доказана.
Закон больших чисел может быть распространен и на зависимые СВ. Обобщение закона больших чисел на случай зависимых СВ принадлежит А.А. Маркову.
Теорема Маркова. Если имеются зависимые СВ Х1, Х2, …, Хn и если при n®¥ 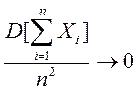 , то среднее арифметическое наблюдаемых значений СВ Х1, Х2, …, Хn сходится по вероятности к среднему арифметическому их МОЖ.
, то среднее арифметическое наблюдаемых значений СВ Х1, Х2, …, Хn сходится по вероятности к среднему арифметическому их МОЖ.
Доказательство: Рассмотрим СВ 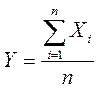 , очевидно
, очевидно
Dy= 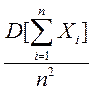 . Применим с СВ Y неравенство Чебышева
. Применим с СВ Y неравенство Чебышева 
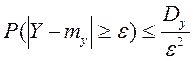 . Так как по условию теоремы при n®¥, Dy®0, то при достаточно большом n
. Так как по условию теоремы при n®¥, Dy®0, то при достаточно большом n 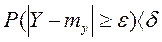 , где d, e - сколь угодно малая положительная величина, или переходя к противоположному событию
, где d, e - сколь угодно малая положительная величина, или переходя к противоположному событию
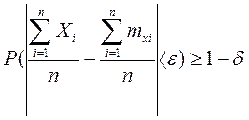 . Теорема доказана.
. Теорема доказана.
3. Следствия закона больших чисел: теоремы Бернулли и Пуассона.
Теорема Я.Бернулли является важнейшей и исторически первой формой закона больших чисел. Он устанавливает связь между частотой события и его вероятностью. Доказательство данное Бернулли было весьма сложным. Простое доказательство дано П.П. Чебышевым – как прямое следствие из его теоремы.
Теорема Бернулли. При неограниченном увеличении числа независимых опытов в постоянных условиях чистоты рассматриваемого события АР* сходится по вероятности к его вероятности Р в отдельном опыте.
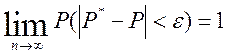
Доказательство: Обозначим Х1 – СВ – число появлений события А в первом опыте, Х2 – СВ – число появлений события А во втором опыте и т.д.
Каждая из величины Хi(i=1, 2, …, n) есть дискретное СВ с двумя возможными значениями 0 и 1. Ряд распределения СВ Хi имеет вид
| Хi | ||
| Рi | q | Р |
, где q=1-Р – вероятность не появления А.
Математическое ожидание каждой из величин Хi равно р, а ее дисперсия qр.
Частота Р* представляет собой среднее арифметическое СВ Х1,Х2, …, Хn 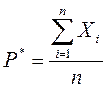 . Применим к этим величинам теорему Чебышева получим
. Применим к этим величинам теорему Чебышева получим
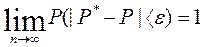 .
.
Обобщением теоремы Бернулли на случай, когда опыты происходят при неодинаковых условиях, является теорема Пуассона, которая формулируется следующим образом.
Теорема Пуассона. При неограниченном увеличении числа независимых опытов в переменных условиях чистоты события А сходится по вероятности к среднему арифметическому его вероятностей Рi при данных испытаниях.
Доказательство теоремы Пуассона следует из обобщенной теоремы Чебышева, точно также, как доказательство теоремы Бернулли следует из теоремы Чебышева.
Дата добавления: 2016-03-05; просмотров: 4146;
