Аксиомы, законы, тождества и теоремы алгебры логики

Цифровые устройства

В схемах импульсной техники для обработки и преобразования информации широко применяют цифровые методы. Они базируются на использовании сигнала прямоугольной формы, имеющего два фик­сированных уровня напряжения. Это позволяет представить сигнал в цифровой форме: уровню высокого напряжения приписывают сим­вол «1», а уровню низкого напряжения — символ «О». На указанном виде сигнала основана, в частности, работа цифровых вычислитель­ных устройств, а также используемая в них двоичная система счисле­ния.

Цифровая форма представления сигнала упрощает рассмотрение импульсных систем и позволяет использовать при их анализе и раз­работке соответствующий математический аппарат (алгебру логики). Цифровые методы построения и проектирования импульсных систем занимают в современной электронике ведущее место.

Математическим аппаратом анализа и синтеза цифровых систем служит алгебра логики (булева алгебра), которая изучает связь между переменными (сигналами), принимающими толь­ко два («0», «1») значения. Символы «0» и «1» в алгебре логики харак­теризуют состояния переменных или состояния их функций, в связи с чем эти символы нельзя рассматривать как арифметические числа. Алгебра логики является алгеброй состоя­ний, а не алгеброй чисел, и для нее характерны основные действия, отличные от принятых в обычной алгебре действий над числами.

Аксиомы, законы, тождества и теоремы алгебры логики

В алгебре логики любая переменная может иметь состояние «0» или «1». Поэтому в алгебре логики каждой двоичной переменной, например x ставится в соответствие обратная или дополнительная к ней (инверсная) переменная, такая, что:

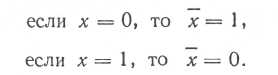
Переменную х (с чертой) следует читать как НЕ х,

В алгебре логики имеется две операции: логическое сложение (дизъюнкция) и логическое умножение (конъюнкция).

Правила логического сложения (+ читается как «или»)

0+0 = 0

0+1 = 1

1+0 = 1

1+1 = 1

Правила логического умножения (• читается как «и»)

0•0 = 0

0•1 = 0

1•0 = 0

1•1 = 1

В алгебре логики в случае одной переменной х действуют следующие правила (аксиомы):

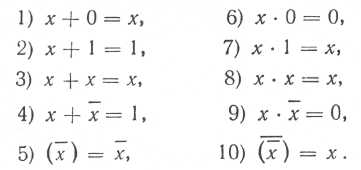
Правила 1—4 характеризуют операцию логического сложения (дизъюнкции), правила 6—9 — операцию логического умножения (конъюнкции) и правила 5,10 — операцию инверсии. Знак логического сложения «+» читается ИЛИ (например, правило 1 : «х или 0 равен х»). Знак логичес­кого умножения « • » читается И (например, «х и 0 равен 0»).

Правила 1—4, 6—9 поясняются схемами (рис. 3.19, а — г) на двух ключах в соответствии с числом слагаемых (сомножителей) в соотно­шениях. Положению «Ключ включен» соответствует состояние «1», а положению «Ключ выключен» — состояние «0». Для логического сложения (правила 1—4) ключи в схемах соединены параллельно. Уровень высокого напряжения на выходе (F = 1) будет иметь место, если хотя бы один ключ находится в состоянии «1» (правила 2, 4; рис. 3.19, б, г). Результат суммы в правилах 1, 3 зависит от значения х

(при х = 1 F = 1, при х = 0 F = 0; рис. 3.19, а, в). Для логического умножения ключи соединены последовательно (рис. 3.19, д — з). Уровень высокого напряжения на выходе (F = 1) будет только в том случае, если оба сомножителя равны единице (оба ключа включены). В противном случае результат умножения равен нулю (правила 6, 9; рис. 3.19, д, з). Результат умножения в правилах 7, 8 зависит от значения х (рис. 3.19, е, ж).

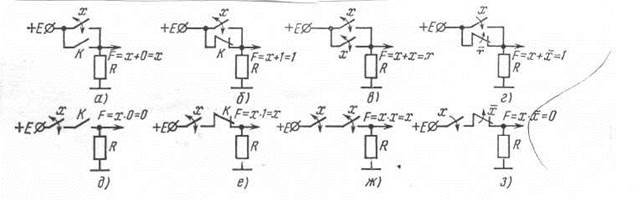
Рис. 3.19. Схемы, иллюстрирующие операции логического сложения (а — г) и логического умножения {д —з)

Для алгебры логики, как и для обычной алгебры, действительны следующие законы.

Переместительный закон (закон коммутатив­ности) для логического сложения и умножения:

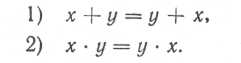
Сочетательный закон (закон ассоциативности) для логического сложения и умножения:

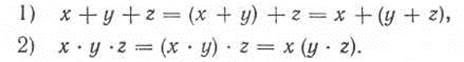
Распределительный закон (закон дистрибутивности логического умножения по отношению к сложению):

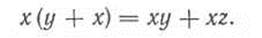
Для многих случаев алгебраических преобразований полезными являются тождества, относящиеся к двум и трем переменным:

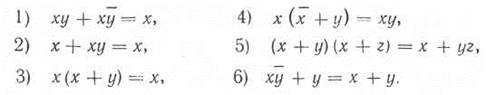
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА ДИОДАХ И БИПОЛЯРНЫХ ТРАНЗИСТОРАХ

Логические элементы (узлы) предназначены для выполнения различных логических (функциональ­ных) операций над дискретными сигналами при двоичном способе их представления.

Преимущественное распространение получили логические эле­менты потенциального типа. В них используются дискрет­ные сигналы, нулевому значению которых соответствует уровень низкого потенциала, а единичному значению — уровень высокого по­тенциала (отрицательного или положительного). Связь потенциаль­ного логического элемента с предыдущим и последующими узлами в системе осуществляется непосредственно, без при­менения реактивных компонентов. Благодаря этому преимуществу именно потенциальные логические элементы наш­ли почти исключительное применение в интегральном исполнении в виде микросхем. С позиций использования логических микросхем потенциального типа и проводится далее рассмотрение логических элементов.

Логические биполярные микросхемы чаще выполняют на транзисторах типа п-р-п с напряжением питания Е_к > 0. Этим объясняет­ся, что используемые здесь сигналы имеют положительную полярность. Уровню высокого положительного потенциала («1») на выходе соответствует закрытое состояние транзистора, а уровню низкого потенциала («0») — его открытое состояние. С этой точки зрения, в частности, и следует понимать действие сигнала на входе логического элемента, имеющего непосредственную связь в другими элементами в конкретной схеме. Для упрощения уровень низкого потенциала сигнала полагаем равным нулю, а процесс перехода транзистора из одного состояния в другое — достаточно быстрым.

Логические интегральные микросхемы являются элементами, на основе которых выполняются схемы цифровой техники.

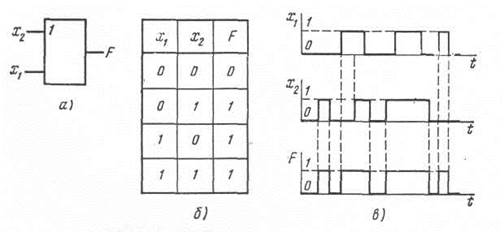
Рис. 3.24. Условное обозначение логического элемента ИЛИ (а), его таблица истинности и временные диаграммы (б, в)

Логический элемент ИЛИ. Логический элемент ИЛИ имеет не­сколько входов и один общий выход. Его условное обозначение пока­зано на рис. 3.24, а.

Логический элемент ИЛИ выполняет операцию логи­ческого сложения (дизъюнкции):

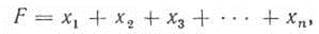
где F — функция; x₁, x₂ , x₃, , x_n— аргументы (переменные, двоич­ные сигналы на входах).

Здесь функция F = 0, когда все ее аргументы равны нулю, и F = 1 при одном, нескольких или всех аргументах, равных единице.

Работу схемы двухвходового логическо­го элемента ИЛИ иллюстрируют таблица истинности и временные диаграммы, при­веденные на рис. 3.24, б, в. Моделью двух­входового элемента ИЛИ может служить схема с двумя параллельно включенными ключами (см. рис. 3.19, а — г). Если оба ключа выключены (аргументы равны ну­лю), то напряжение на выход.1 равно нулю и F — 0. При одном или двух включенных ключах напряжение на выходе равно Е и F = 1.

Наиболее просто элемент ИЛИ реали­зуется на диодах (рис. 3.25). Значение F = 1 на выходе создается передачей входного сигнала вследствие отпирания соответствующего диода. К диодам, для которых входной сигнал равен нулю, прикладывается обратное напряжение, и они находятся в закрытом состоянии.

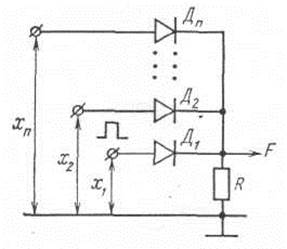
Рис. 3.25. Схема логического элемента ИЛИ на диодах

Логический элемент И. Логический элемент И также имеет не­сколько входов и один выход. Его условное обозначение показано на рис. 3.26, а.

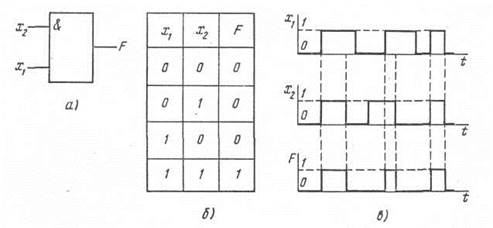
Рис. 3.26. Условное обозначение логического элемента И (а), его таблица истинности и временные диаграммы (б, в)

Логический элемент И выполняет операцию логиче­ского умножения (конъюнкции):

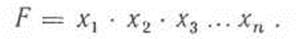
Здесь функция F = 0, когда хотя бы один из ее аргументов равен нулю, и F = 1 при всех аргументах, равных единице.

Работу схемы двухвходового логического элемента И иллюстри­руют таблица истинности и временные диаграммы, приведенные на рис. 3.26, б, в.

Элемент И является схемой совпадения: сигнал «1» на выходе появляется при совпадении сигналов «1» на всех входах. Моделью двухвходового элемента И может служить схема с двумя последовательно включенными ключами и источником питания (см. рис. 3.19, д — з).

Простейшая схема элемента И на диодах приведена на рис. 3.27.

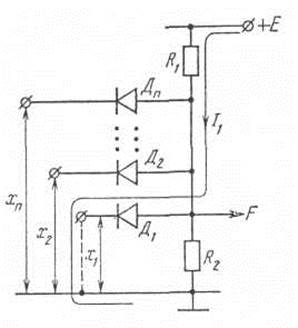
Рис. 3.27. Схема логического элемента И на диодах

Отличие от схемы элемента ИЛИ (см. рис. 3.25) заключается в изменении полярности включения диодов и наличии резистора R₁, подключенного к шине «+» источника питания.

Схема работает следующим образом. При всех входных сигналах, равных единице, на катодах диодов имеется положительный потенциал относительно общей точки и все диоды закрыты. На выходе схе­мы создается напряжение, определяющее F = 1. При нулевом значении сигнала хотя бы на одном из входов соответ­ствующий диод будет проводить ток и шунтировать резистор R2, выполняющий, как и резистор R в схеме рис. 3.25, роль нагрузки. На­пряжение на выходе при этом определяется падением напряжения на открытом диоде и близко к нулю (F = 0). На рис. 3.27 показан вариант, когда х₁ = 0 и проводит ток диод Д₁. Увеличение числа входов с нулевым значением сигнала приво­дит только к увеличению числа проводящих диодов, а функция F остается равной нулю.

Логический элемент НЕ. Логический элемент НЕ имеет один вход и один выход. Его условное обозначение показано на рис. 3.28, а.

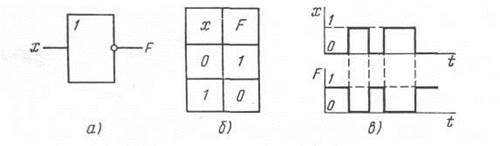
Рис. 3.28. Условное обозначение логического элемен­та НЕ (а), его таблица истинности и временные диа­граммы (б, в)

Элемент НЕ выполняет операцию инверсии (отрицания), в связи с чем его часто называют логическим инвертором. Им реализуется функция

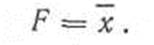
Сигналу х = 0 на входе соответствует F = 1 и, наоборот, при х =1 F = 0.

Работу схемы логического элемента НЕ иллюстрируют таблица истинности и временные диаграммы, приведенные на рис. 3.28, б, в.

Логический элемент НЕ представляет собой ключевую схему на транзисторе (рис. 3.29).

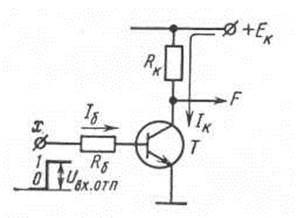
Рис. 3.29. Схема логического элемента НЕ

. При х = 0 (U_BX =0) транзистор закрыт, напряжение U_кэ≈ Е_к т. е. F = 1. При х = 0 транзистор открыт, т.е. F = 0. Открытое состояние транзистора обеспечивается заданием тока базы, вводящего транзистор в режим насыщения.

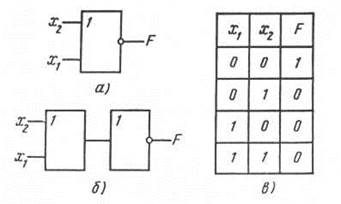
Рис. 3.30. Условное обозначение логи­ческого элемента ИЛИ — НЕ (а), его функциональный эквивалент (б) и таб­лица истинности (в)

Логический элемент ИЛИ — НЕ. Условное обозначение логичес­кого элемента ИЛИ — НЕ показано на рис. 3.30, а. Он объединяет элементы ИЛИ и НЕ с очередностью проведения операций, показан­ной на рис. 3.30, б. В связи с этим входным сигналам, равным едини­це, соответствует логический «0» на выходе, а при нулевых сигналах на всех входах F = 1. Для двухвходового элемента ИЛИ — НЕ ука­занное иллюстрирует таблица истинности, приведенная на рис. 3.30, в.

Функциональная операция, выполняемая элементом ИЛИ — НЕ при nвходах, определяется выражением

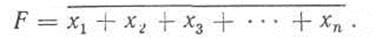
На рис. 3.31, а приведена схема логического элемента ИЛИ — НЕ, представляющая собой последовательное соединение элемента ИЛИ на диодах и элемента НЕ. Логические схемы подобного сочетания опре­деляют, в частности, класс элементов так называемой диодно-транзисторной логики (ДТЛ). Принцип действия эле­мента ясен из диаграмм рис. 3.31, б, где показаны сигналы х₁, и х₂ на входах, сигнал у на выходе элемента ИЛИ и выходная функция F.

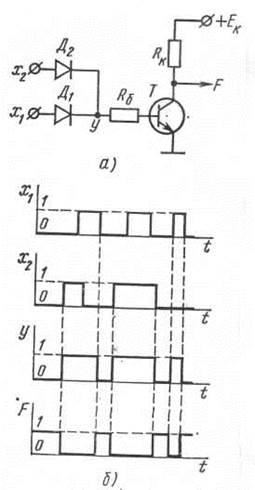
Рис. 3.31. Схема логи­ческого элемента ИЛИ__

НЕ ДТЛ (а) и его вре­менные диаграммы (б)

Логический элемент И — НЕ. Условное обозначение логического элемента И — НЕ показано на рис. 3.32, а.

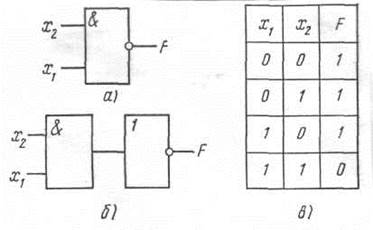
Рис. 3.32. Условное обозначение логи­ческого элемента И — НЕ (а),

его функ­циональный эквивалент (б) и таблица истинности (в)

Ему эквивалентна структурная схема, показанная на рис 3.32, б. Логической «1» на всех информационных входах соответствует логический «0» на вы­ходе элемента. При логическом «0» на од­ном из входов создается логическая «1» на выходе. Для двухвходового элемента И — НЕ сказанное отражено в таблице истин­ности на рис. 3.32, в. Логическая функция элемента И — НЕ при п входах отвечает выражению

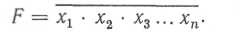
На рис. 3.34 приведена схема элемента И— НЕ, реализован­ная на транзисторах Схемы такого типа образуют класс элементов так называемой транзисторно-транзисторной логики (ТТЛ).

Основой этого класса элементов является использование многоэмиттерного транзистора Тм. Транзистор на входе применен вместо диодов (в предыдущих схемах).

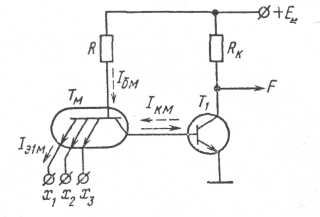
Рис. 3.34. Схема логического эле­мента И — НЕ ТТЛ

Подобная замена технологически выгодна, поскольку изготовление многоэмиттерного транзистора в микросхемах не намно­го сложнее, чем изготовление обычного транзистора, а площадь, занимаемая многоэмиттерным транзистором в кристалле полупровод­ника, меньше диодной части элемента И — НЕ ДТЛ. От обычного транзистора многоэмиттерный транзистор отличается наличием не­скольких (например, трех) эмиттерных областей с общими для всего транзистора базовым и коллекторным слоями.

При комбинации входных сигналов, когда на одном из входов (например x₁) действует нулевое напряжение (x₁ = 0), ток через ре­зистор R замыкается по цепи эмиттера этого входа. В базу транзи­стора T1 ток эмиттера I_э1м не ответвляется, так как для направления тока I_км (указано на рис 3.34 пунктирной стрелкой) сопротив­ление база — эмиттер транзистора Т1, довольно велико. Транзистор Т1 закрыт. Сигнал на выходе F = 1. Так будет и при нулевом сигнале на большем числе входов элемента.

При наличии на всех входах логической «1» (напряжений, близ­ких к + Ек) все эмиттерные переходы транзистора Тм будут находить­ся под обратным напряжением, а коллекторный переход — под прямым. Ток I_бм будет обусловливать ток I_км, направление которого показано на рис. 3.34 сплошной стрелкой- Транзистор Т1 будет от­крыт, его сигнал F = 0. Таким образом, схема рис. 3.34 выполняет логическую операцию И — НЕ.

Наличие усилительного элемента — транзистора — в логических микросхемах ИЛИ — НЕ и И — НЕ классов ДТЛ и ТТЛ определяет такое их важное преимущество, как сохранение неизменного уровня напряжения, соответствующего логической «1», в процессе передачи сигнала при их последовательном соединении. В связи с этим указан­ные элементы, а также элемент НЕ являются базовыми в микросхемотехнике. В общем корпусе выпускаемых микросхем обычно содержится несколько элементов одного типа.

Параметры логических элементов. К основным параметрам логи­ческих элементов (логических микросхем) относятся функциональ­ные возможности элемента, быстродействие, потребляемая мощность и помехоустойчивость.

Функциональные возможности логического элемента определяются коэффициентом разветвления n по выходу и коэффициентом обьедннения m по входу. Под коэффициентом разветвления логического элемента по­нимают количество входов аналогичных элементов, которое может быть подключено к его выходу, а под коэффициентом объединения - число входов, которое может иметь элемент. Иными словами, коэффициент n характеризует нагрузочную способность микросхем.

Чем выше коэффициенты n иm, тем меньшее количество микросхем потребуется для создания конкретного устройства. Препятствием к увеличению коэффициента n является ухудшение других пока­зателей элемента (помехоустойчивости, быстродействия) или наруше­ние нормального режима его работы.

Нагрузочная способность активного логического элемента суще­ственно зависит от типа используемого в нем выходного транзистор­ного каскада (инвертора). Как правило, для большинства типов ин­тегральных микросхем коэффициент n не превышает 4—10. Для уве­личения нагрузочной способности к выходу элемента в случае необ­ходимости подключают так называемый буферный усилитель с мощным многотранзисторным инвертором, позволяющим получить n = 20 — 50. Буферный усилитель входит в состав серии интегральных мик­росхем.

В существующих сериях интегральных микросхем основные логи­ческие элементы (ИЛИ - НЕ, И — НЕ) выполняются, как правило, с небольшим числом входов (m = 2 - 6). С целью увеличения коэф­фициента m применяют схему логического расширителя, подключе­ние которой к основным элементам ИЛИ — НЕ, И — НЕ позволяет увеличить коэффициент m до 10 и более. Функцию логического расши­рителя в схемах, например И - НЕ ДТЛ, выполняют дополнитель­ные диоды, подключаемые параллельно основным диодам элемента (см. рис. 3.-33, а):—

Быстродействие характеризует время реакции логичес­кого элемента на изменение сигналов на входах.

Показателем быстродействия логических микросхем является среднее время задержки прохождения сигнала через элемент : t_з.c

Логические микросхемы подразделяются на сверхбыстродейст­вующие (t_з.c. < 0,01 мкс), быстродействующие «t_з.c < 0,01 - 0,03 мкс), среднего быстродействия (t_з.c < 0,03 - 0,3 мкс), низкого быстродей­ствия (t_з.c > 0,3 мкс).

Существенным параметром логических элементов является также потребляемая мощность от источника питания. В зависимости от типа (серии) мощность, потребляемая логической микросхемой, составляет 250 мВт — 1 мкВт. Ее обычно определяют по средней мощности, потребляемой элементом в состояниях «0» и «1». Потребляемая мощность связана с быстродействием микросхем. В частности, микросхемы, потребляющие большую мощность, отли­чаются, как правило, и высоким быстродействием.

Помехоустойчивость характеризует меру невосприимчивости логических элементов к изменению своих состояний под воз­действием напряжения помех. Помехи, действующие на входе логической микросхемы, подразделяются на статические и импульсные (статическая и импульсная помехоустойчивость). Статическими назы­вают помехи, напряжение которых остается постоянным в течение времени, значительно превышающего длительность переходных про­цессов в схеме. Причиной их появления являются падения напряжения в проводниках, соединяющих микросхемы в устройстве. Статическая помехоустойчивость характеризуется максимальным напряжением помехи, которое может быть подано на вход логического эле­мента, не вызывая при этом его ложного срабатывания.

Импульсные помехи обусловливаются различными наводками от соседних работающих установок. По аналогии со статической помехо­устойчивостью импульсная помехоустойчивость характеризуется напряжением импульса, величина которого зависит от формы и длительности импульса.

К действию помех наиболее чувствительны микросхемы, имеющие низкий перепад логических уровней. На помехоустойчивость оказывают влияние вид схем, режим работы транзисторов, напряжение источников питания и т. д.

Для уменьшения влияния помех необходимо рационально компоновать корпусы микросхем на печатных платах, осуществлять соответствующие развязки по цепям напряжений питания, а в некоторых случаях экранировать цепи связи между элементами или отдельные блоки.

Типы логических элементов. В современных интегральных микросхемах находят применение различные типы логических элементов. Мы уже рассмотрели построение логических элементов на диодно-транзисторной логике (ДТЛ) и транзисторно-транзисторной логике (ТТЛ).

Для увеличения быстродействия в ТТЛ-логику часто вводят диоды Шоттки, имеющие отрицательный участок ВАХ, что приводит к увеличению быстродействия (ТТЛШ).

Также для увеличения быстродействия применяют устройства эмиттерно-связанной логики (ЭСЛ), в основу которой входят токовые ключи с объединенными эмиттерами (их схема очень похожа на входной каскад дифференциального усилителя).

Значительно уменьшить потребляемую мощность логических элементов позволяет использование в них полевых транзисторов с разными типами каналов, т.н. комплементарных транзисторов, не потребляющих энергию в статическом режиме, а имеющих потребление энергии только при переключениях. Такая логика носит название КМОП.

Еще одним типом логических элементов является интегральная инжекционная логика (И²Л). Она использует биполярные транзисторы, обладающие все же лучшими (по сравнению с полевыми) ключевыми и частотными свойствами.

Благодаря особым схемотехническим решениям – отсутствию резисторов, использованию токового принципа питания, а также очень компактного расположения элементов, удается значительно сократить объем элементов, уменьшить потребление и повысить быстродействие.