Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логические операции над высказываниями
Операции над высказываниями
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание – это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.
Так, например, предложение «6 – четное число» следует считать высказыванием, истинным. Предложение «Рим – столица Франции» тоже высказывание, но ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения «ученик десятого класса» и «информатика – интересный предмет». Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределенное понятие «интересный предмет». Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа «в городе A более миллиона жителей», «у него голубые глаза» не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если..то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Bысказывания, образованные из других с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Так, например, из элементарных высказываний «Петров – врач», «Петров – шахматист» при помощи связки «и» можно получить составное высказывание «Петров – врач и шахматист», понимаемое как «Петров – врач, хорошо играющий в шахматы».
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание «Тимур поедет летом на море», а через В – высказывание «Тимур летом отправится в горы». Тогда составное высказывание «Тимур летом побывает и на море, и в горах» можно кратко записать как А и В. Здесь «и» – логическая связка, А, В – логические переменные, которые мoгут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
1)Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком « 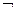 »). Высказывание
»). Высказывание 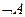 или
или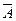 истинно, когда A ложно, и ложно, когда A истинно. Например: «Луна – спутник Земли» (А); «Луна – не спутник Земли» (
истинно, когда A ложно, и ложно, когда A истинно. Например: «Луна – спутник Земли» (А); «Луна – не спутник Земли» (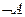 ).
).
2) Операция, выражаемая связкой «и», называется конъюнкцией или логическим умножением и обозначается « 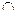 » (может также обозначаться знаками «&,
» (может также обозначаться знаками «&, 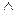 »). Высказывание
»). Высказывание 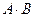 истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание «10 делится на 2 и 5 больше 3» истинно, а высказывания «10 делится на 2 и 5 не больше 3», «10 не делится на 2 и 5 больше 3», «10 не делится на 2 и 5 не больше 3» – ложны.
истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание «10 делится на 2 и 5 больше 3» истинно, а высказывания «10 делится на 2 и 5 не больше 3», «10 не делится на 2 и 5 больше 3», «10 не делится на 2 и 5 не больше 3» – ложны.
3) Операция, выражаемая связкой «или», называется дизъюнкцией или логическим сложением и обозначается знаками «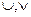 ». Высказывание
». Высказывание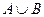 ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание «10 не делится на 2 или 5 не больше 3» ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3» – истинны.
ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание «10 не делится на 2 или 5 не больше 3» ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3» – истинны.
4)Операция, выражаемая связками «если ... то»,«из ... следует», «…влечет ...», называется импликацией и обозначается знаками 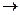 ,
,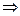 . Высказывание
. Высказывание 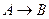 ложно тогда и только тогда, когда А истинно, а В ложно.
ложно тогда и только тогда, когда А истинно, а В ложно.
5)Операция, выражаемая союзом «либо», называется строгой дизъюнкцией (исключающим «или», сложением по модулю 2), обозначается знаками 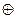 ,
,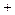 . Высказывание
. Высказывание 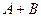 ложно, когда А и В оба истинны, или оба ложны.
ложно, когда А и В оба истинны, или оба ложны.
Рассмотрим высказывания: «данный четырехугольник – квадрат» (А) и «около данного четырехугольника можно описать окружность» (В), тогда составное высказывание 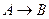 читается как: «если данный четырехугольник квадрат, то около него можно описать окружность». Высказывание
читается как: «если данный четырехугольник квадрат, то около него можно описать окружность». Высказывание 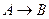 истинно, когда:
истинно, когда:
а) А истинно и В истинно, то есть данный четырехугольник квадрат, и около него можно описать окружность;
б) А ложно и В истинно, то есть данный четырехугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырехугольника);
с) A ложно и B ложно, то есть данный четырехугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырехугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка «если ... то» описывает причинно-следственную связь между высказываниями, однако в логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность. Поэтому не надо смущаться «бессмысленностью» импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: «если президент США – демократ, то в Африке водятся жирафы», «если арбуз – ягода, то в бензоколонке есть бензин».
6)Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно ...», называется эквиваленцией или двойной импликацией и обозначается знаком « 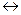 » (или «
» (или « 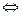 »). Высказывание
»). Высказывание 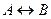 истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 3»и«23 делится на 6 тогда и только тогда, когда 23 делится на 3» истинны, а высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 5», «21 делится на 6 тогда и только тогда, когда 21 делится на 3» – ложны. Высказывания А и В, образующие составное высказывание, могут быть совершенно не связаны по содержанию, например: «три больше двух» (А), «пингвины живут в Антарктиде» (В). Отрицаниями этих высказываний являются высказывания «три не больше двух», «пингвины не живут в Антарктиде».
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 3»и«23 делится на 6 тогда и только тогда, когда 23 делится на 3» истинны, а высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 5», «21 делится на 6 тогда и только тогда, когда 21 делится на 3» – ложны. Высказывания А и В, образующие составное высказывание, могут быть совершенно не связаны по содержанию, например: «три больше двух» (А), «пингвины живут в Антарктиде» (В). Отрицаниями этих высказываний являются высказывания «три не больше двух», «пингвины не живут в Антарктиде».
Установим вид следующих предложений:
a) «Москва является столицей России» – истинное высказывание;
b) «Берлин находится во Франции» – ложное высказывание;
c) «Как тебя зовут?» – не высказывание;
d) «Земля является планетой Солнечной системы» – истинное высказывание;
e) «2+8<5» – ложное высказывание;
f) «5·5=25» – истинное высказывание;
g) «Всякий квадрат есть параллелограмм» – истинное высказывание;
h) «Каждый параллелограмм есть квадрат» – ложное высказывание;
i) «Назовем медианой отрезок, соединяющий вершину треугольника с серединой противоположной стороны» – не высказывание, так как определения не бывают истинными или ложными, а фиксируют принятое использование терминов;
j) «Он сероглаз» – высказывательная форма;
k) «х 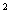 –4х+3=0» – высказывательная форма.
–4х+3=0» – высказывательная форма.
Можно составить формулу для любого сложного высказывания, составному предложению«На улице лето, стоит жара» соответствует формула: 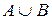 .
.
Упражнения
1. Определить вид высказываний и составить к ним отрицания:
«Зайцы живут в лесу»; «Зря ты так говоришь»; «Хочу петь»; «Солнце – спутник Земли».
2.Определить, для какого числа Х истинно высказывание:
((Х>2) or (X<2)) Þ X>4); ((Х>3) or (X<3)) Þ (X<1).
3. Найти значения логических выражений:
(0Ú 1)Ú (1Ú 0); (0Ù1)Ù 1.
4.Даны простые высказывания: А: «Петя умеет плавать», В: «Сергей умеет прыгать», С: «Алеша умеет стрелять». Прочтите формулы сложных высказываний, составленные из этих простых:
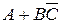 ;
; 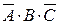 ;
; 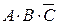 ;
; 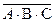 .
.
5. Даны простые высказывания:«Данное число не кратно 3»; «Данное число больше 50». Прочтите сложные высказывания: 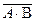 ;
; 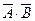 .
.
6. Определить значения истинности высказываний:
а) «Если 16 делится на 4, то 16 делится на 2»;
б) «Если 17 делится на 4, то 17 делится на 2»;
в) «Если 18 делится на 4, то 18 делится на 2»;
г) «Если 18 делится на 2, то 18 делится на 4»;
д) «Если 2· 2=5, то 83 ↔ 500»;
е) «Если 2· 2=4, то 72 =81»;
ж) «Если телепатия существует, то некоторые физические законы требуют пересмотра»;
з) «16 делится на 4 тогда и только тогда, когда 16 делится на 2»;
и) «17 делится на 4 тогда и только тогда, когда 17 делится на 2»;
к) «18 делится на 4 тогда и только тогда, когда 18 делится на 2»;
л) «15 делится на 5 тогда и только тогда, когда 15 делится на 10».
Дата добавления: 2016-04-11; просмотров: 4465;
